Kalman Filtering
This example shows how to perform Kalman filtering. First, you design a steady-state filter using the kalman command. Then, you simulate the system to show how it reduces error from measurement noise. This example also shows how to implement a time-varying filter, which can be useful for systems with nonstationary noise sources.
Steady-State Kalman Filter
Consider the following discrete plant with Gaussian noise w on the input and measurement noise v on the output:
The goal is to design a Kalman filter to estimate the true plant output based on the noisy measurements . This steady-state Kalman filter uses the following equations for this estimation.
Time update:
Measurement update:
Here,
is the estimate of , given past measurements up to .
and are the estimated state values and measurement, updated based on the last measurement .
and are the optimal innovation gains, chosen to minimize the steady-state covariance of the estimation error, given the noise covariances , , and . (For details about how these gains are chosen, see
kalman.)
(These update equations describe a current type estimator. For information about the difference between current estimators and delayed estimators, see kalman.)
Design the Filter
You can use the kalman function to design this steady-state Kalman filter. This function determines the optimal steady-state filter gain M for a particular plant based on the process noise covariance Q and the sensor noise covariance R that you provide. For this example, use the following values for the state-space matrices of the plant.
A = [1.1269 -0.4940 0.1129
1.0000 0 0
0 1.0000 0];
B = [-0.3832
0.5919
0.5191];
C = [1 0 0];
D = 0;For this example, set , meaning that the process noise w is additive input noise. Also, set , meaning that the input noise w has no direct effect on the output y. These assumptions yield a simpler plant model:
When H = 0, it can be shown that (see kalman). Together, these assumptions also simplify the update equations for the Kalman filter.
Time update:
Measurement update:
To design this filter, first create the plant model with an input for w. Set the sample time to -1 to mark the plant as discrete (without a specific sample time).
Ts = -1; sys = ss(A,[B B],C,D,Ts,'InputName',{'u' 'w'},'OutputName','y'); % Plant dynamics and additive input noise w
The process noise covariance Q and the sensor noise covariance R are values greater than zero that you typically obtain from studies or measurements of your system. For this example, specify the following values.
Q = 2.3; R = 1;
Use the kalman command to design the filter.
[kalmf,L,~,Mx,Z] = kalman(sys,Q,R);
This command designs the Kalman filter, kalmf, a state-space model that implements the time-update and measurement-update equations. The filter inputs are the plant input u and the noisy plant output y. The first output of kalmf is the estimate of the true plant output, and the remaining outputs are the state estimates .
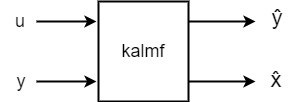
For this example, discard the state estimates and keep only the first output, .
kalmf = kalmf(1,:);
Use the Filter
To see how this filter works, generate some data and compare the filtered response with the true plant response. The complete system is shown in the following diagram.
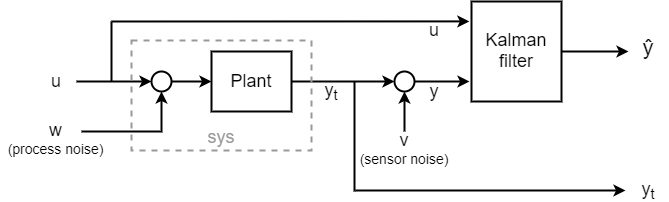
To simulate this system, use a sumblk to create an input for the measurement noise v. Then, use connect to join sys and the Kalman filter together such that u is a shared input and the noisy plant output y feeds into the other filter input. The result is a simulation model with inputs w, v, and u and outputs yt (true response) and ye (the filtered or estimated response ). The signals yt and ye are the outputs of the plant and the filter, respectively.
sys.InputName = {'u','w'};
sys.OutputName = {'yt'};
vIn = sumblk('y=yt+v');
kalmf.InputName = {'u','y'};
kalmf.OutputName = 'ye';
SimModel = connect(sys,vIn,kalmf,{'u','w','v'},{'yt','ye'});To simulate the filter behavior, generate a known sinusoidal input vector.
t = (0:100)'; u = sin(t/5);
Generate process noise and sensor noise vectors using the same noise covariance values Q and R that you used to design the filter.
rng(10,'twister');
w = sqrt(Q)*randn(length(t),1);
v = sqrt(R)*randn(length(t),1);Finally, simulate the response using lsim.
out = lsim(SimModel,[u,w,v]);
lsim generates the response at the outputs yt and ye to the inputs applied at w, v, and u. Extract the yt and ye channels and compute the measured response.
yt = out(:,1); % true response ye = out(:,2); % filtered response y = yt + v; % measured response
Compare the true response with the filtered response.
clf subplot(211), plot(t,yt,'b',t,ye,'r--'), xlabel('Number of Samples'), ylabel('Output') title('Kalman Filter Response') legend('True','Filtered') subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'), xlabel('Number of Samples'), ylabel('Error') legend('True - measured','True - filtered')

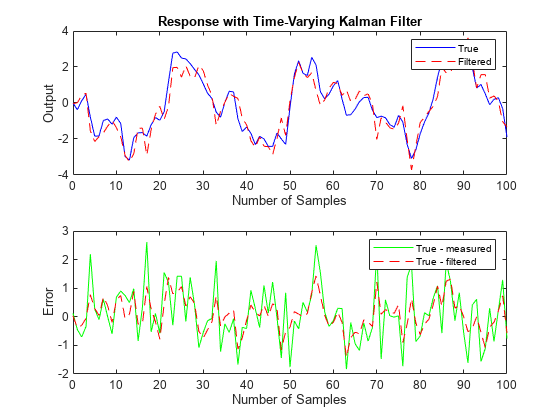
As the second plot shows, the Kalman filter reduces the error yt - y due to measurement noise. To confirm this reduction, compute the covariance of the error before filtering (measurement error covariance) and after filtering (estimation error covariance).
MeasErr = yt - y; MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)
MeasErrCov = 0.9871
EstErr = yt - ye; EstErrCov = sum(EstErr.*EstErr)/length(EstErr)
EstErrCov = 0.3479
Time-Varying Kalman Filter Design
The previous design assumed that the noise covariances do not change over time. A time-varying Kalman filter can perform well even when the noise covariance is not stationary.
The time-varying Kalman filter has the following update equations. In the time-varying filter, both the error covariance and the innovation gain can vary with time. You can modify the time and measurement update equations to account for time variation as follows, again taking so that the process noise w is additive input noise.
Time update:
Measurement update:
See kalman for more detail on these expressions.
In Simulink®, you can implement a time-varying Kalman filter using the Kalman Filter block (see State Estimation Using Time-Varying Kalman Filter).
To create the time-varying Kalman filter in MATLAB®, first, generate the noisy plant response. Simulate the plant response to the input signal u and process noise w defined previously. Then, add the measurement noise v to the simulated true response yt to obtain the noisy response y. In this example, the covariances of the noise vectors w and v do not change with time. However, you can use the same procedure for nonstationary noise.
yt = lsim(sys,[u w]); y = yt + v;
Next, implement the recursive filter update equations in a for loop.
P = B*Q*B'; % Initial error covariance x = zeros(3,1); % Initial condition on the state ye = zeros(length(t),1); ycov = zeros(length(t),1); errcov = zeros(length(t),1); for i=1:length(t) % Measurement update Mxn = P*C'/(C*P*C'+R); x = x + Mxn*(y(i)-C*x); % x[n|n] P = (eye(3)-Mxn*C)*P; % P[n|n] ye(i) = C*x; errcov(i) = C*P*C'; % Time update x = A*x + B*u(i); % x[n+1|n] P = A*P*A' + B*Q*B'; % P[n+1|n] end
Compare the true response with the filtered response.
subplot(211), plot(t,yt,'b',t,ye,'r--') xlabel('Number of Samples'), ylabel('Output') title('Response with Time-Varying Kalman Filter') legend('True','Filtered') subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'), xlabel('Number of Samples'), ylabel('Error') legend('True - measured','True - filtered')
The time-varying filter also estimates the output covariance during the estimation. Because this example uses stationary input noise, the output covariance tends to a steady-state value. Plot the output covariance to confirm that the filter has reached a steady state.
figure plot(t,errcov) xlabel('Number of Samples'), ylabel('Error Covariance'),
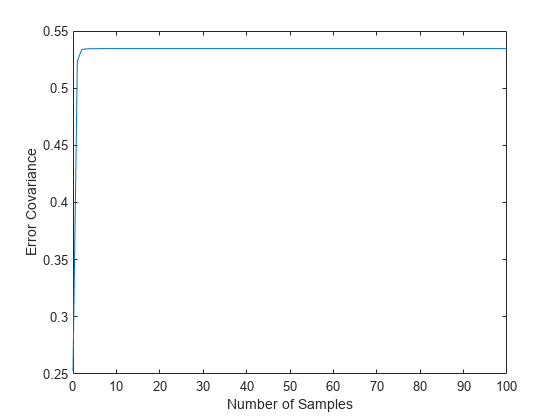
From the covariance plot, you can see that the output covariance reaches a steady state in about five samples. From then on, the time-varying filter has the same performance as the steady-state version.
As in the steady-state case, the filter reduces the error due to measurement noise. To confirm this reduction, compute the covariance of the error before filtering (measurement error covariance) and after filtering (estimation error covariance).
MeasErr = yt - y; MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)
MeasErrCov = 0.9871
EstErr = yt - ye; EstErrCov = sum(EstErr.*EstErr)/length(EstErr)
EstErrCov = 0.3479
Finally, when the time-varying filter reaches steady state, the values in the gain matrix Mxn match those computed by kalman for the steady-state filter.
Mx,Mxn
Mx = 3×1
0.5345
0.0101
-0.4776
Mxn = 3×1
0.5345
0.0101
-0.4776
More About Kalman Filters
For more information about Kalman filters, play the video, or watch the rest of the series at Understanding Kalman Filters — MATLAB Tech Talks.