PID Controller Design at the Command Line
This example shows how to design a PID controller for the plant given by:
As a first pass, create a model of the plant and design a simple PI controller for it.
sys = zpk([],[-1 -1 -1],1);
[C_pi,info] = pidtune(sys,'PI')C_pi =
1
Kp + Ki * ---
s
with Kp = 1.14, Ki = 0.454
Continuous-time PI controller in parallel form.
Model Properties
info = struct with fields:
Stable: 1
CrossoverFrequency: 0.5205
PhaseMargin: 60.0000
C_pi is a pid controller object that represents a PI controller. The fields of info show that the tuning algorithm chooses an open-loop crossover frequency of about 0.52 rad/s.
Examine the closed-loop step response (reference tracking) of the controlled system.
T_pi = feedback(C_pi*sys, 1); step(T_pi)
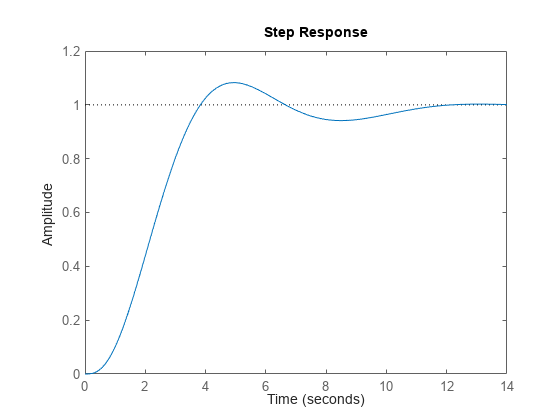
To improve the response time, you can set a higher target crossover frequency than the result that pidtune automatically selects, 0.52. Increase the crossover frequency to 1.0.
[C_pi_fast,info] = pidtune(sys,'PI',1.0)C_pi_fast =
1
Kp + Ki * ---
s
with Kp = 2.83, Ki = 0.0495
Continuous-time PI controller in parallel form.
Model Properties
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 43.9973
The new controller achieves the higher crossover frequency, but at the cost of a reduced phase margin.
Compare the closed-loop step response with the two controllers.
T_pi_fast = feedback(C_pi_fast*sys,1); step(T_pi,T_pi_fast) axis([0 30 0 1.4]) legend('PI','PI,fast')
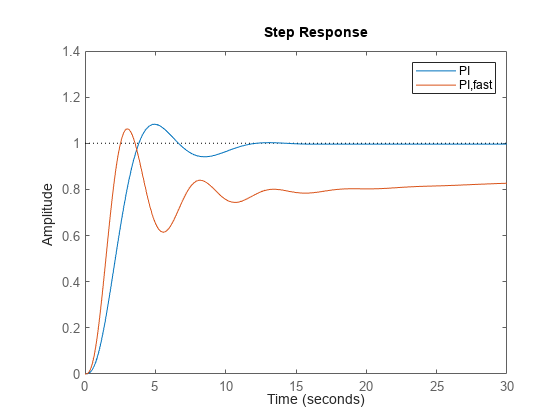
This reduction in performance results because the PI controller does not have enough degrees of freedom to achieve a good phase margin at a crossover frequency of 1.0 rad/s. Adding a derivative action improves the response.
Design a PIDF controller for Gc with the target crossover frequency of 1.0 rad/s.
[C_pidf_fast,info] = pidtune(sys,'PIDF',1.0)C_pidf_fast =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 2.72, Ki = 0.985, Kd = 1.72, Tf = 0.00875
Continuous-time PIDF controller in parallel form.
Model Properties
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 60.0000
The fields of info show that the derivative action in the controller allows the tuning algorithm to design a more aggressive controller that achieves the target crossover frequency with a good phase margin.
Compare the closed-loop step response and disturbance rejection for the fast PI and PIDF controllers.
T_pidf_fast = feedback(C_pidf_fast*sys,1); step(T_pi_fast, T_pidf_fast); axis([0 30 0 1.4]); legend('PI,fast','PIDF,fast');

You can compare the input (load) disturbance rejection of the controlled system with the fast PI and PIDF controllers. To do so, plot the response of the closed-loop transfer function from the plant input to the plant output.
S_pi_fast = feedback(sys,C_pi_fast); S_pidf_fast = feedback(sys,C_pidf_fast); step(S_pi_fast,S_pidf_fast); axis([0 50 0 0.4]); legend('PI,fast','PIDF,fast');

This plot shows that the PIDF controller also provides faster disturbance rejection.