Validate Online State Estimation in Simulink
After you use the Extended Kalman Filter, Unscented Kalman Filter or Particle Filter blocks for online state estimation of a nonlinear system, validate the estimation before deploying the code in your application. If the validation indicates low confidence in the estimation, then see Troubleshoot Online State Estimation for next steps. After you have validated the online estimation results, you can generate C/C++ code for the blocks using Simulink® Coder™ software.
To validate the performance of your filter, perform state estimation using measured or simulated output data from these scenarios.
Obtain output data from your system at different operating conditions and input values — To ensure that estimation works well under all operating conditions of interest. For example, suppose that you want to track the position and velocity of a vehicle using noisy position measurements. Measure the data at different vehicle speeds and slow and sharp maneuvers.
For each operating condition of interest, obtain multiple sets of experimental or simulated data with different noise realizations — To ensure that different noise values do not deteriorate estimation performance.
For each of these scenarios, test the filter performance by examining the residuals and state estimation error.
Examine Residuals
The residual, or output estimation error, is the difference
between the measured system output yMeasured[k],
and the estimated system output yPredicted[k|k-1] at
time step k. Here, yPredicted[k|k-1] is
the estimated output at time step k, which is predicted
using output measurements until time step k-1.
The blocks do not explicitly output yPredicted[k|k-1],
however you can compute the output using the estimated state values
and your state transition and measurement functions. For an example,
see Compute Residuals and State Estimation Errors.
The residuals must have the following characteristics:
Small magnitude — Small errors relative to the size of the outputs increase confidence in the estimated values.
Zero mean
Low autocorrelation, except at zero time lag — To compute the autocorrelation, you can use the Autocorrelation (DSP System Toolbox) block from DSP System Toolbox™ software.
Examine State Estimation Error for Simulated Data
When you simulate the output data of your nonlinear system and use that data for state estimation, you know the true state values. You can compute the errors between estimated and true state values and analyze the errors. The estimated state value at any time step is output at the xhat port of the blocks. The state estimation errors must satisfy the following characteristics:
Small magnitude
Zero mean
Low autocorrelation, except at zero time lag
You can also compute the covariance of the state estimation error, and compare it to the state estimation error covariance that is output by the blocks in the P port of the blocks. Similar values increase confidence in the performance of the filter.
Compute Residuals and State Estimation Errors
This example shows how to estimate the states of a discrete-time Van der Pol oscillator and compute state estimation errors and residuals for validating the estimation. The residuals are the output estimation errors, that is, they are the difference between the measured and estimated outputs.
In the Simulink® model vdpStateEstimModel, the Van der Pol Oscillator block implements the oscillator with nonlinearity parameter, mu, equal to 1. The oscillator has two states. A noisy measurement of the first state x1 is available.
The model uses the Unscented Kalman Filter block to estimate the states of the oscillator. Since the block requires discrete-time inputs, the Rate Transition block samples x1 to give the discretized output measurement yMeasured[k] at time step k. The Unscented Kalman Filter block outputs the estimated state values xhat[k|k] at time step k, using yMeasured until time k. The filter block uses the previously written and saved state transition and measurement functions, vdpStateFcn.m and vdpMeasurementFcn.m. For information about these functions, see Nonlinear State Estimation Using Unscented Kalman Filter and Particle Filter.
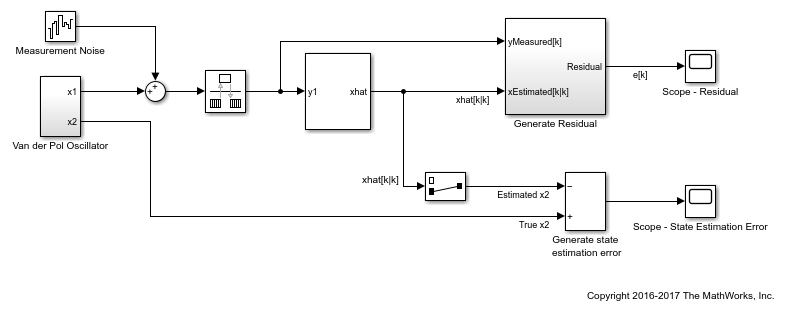
To validate the state estimation, the model computes the residuals in the Generate Residual block. In addition, since the true state values are known, the model also computes the state estimation errors.
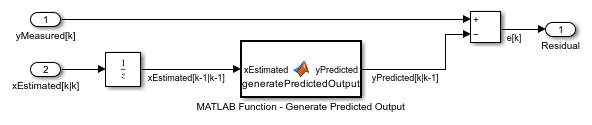
To compute the residuals, the Generate Residual block first computes the estimated output yPredicted[k|k-1] using the estimated states and state transition and measurement functions. Here, yPredicted[k|k-1] is the estimated output at time step k, predicted using output measurements until time step k-1. The block then computes the residual at time step k as yMeasured[k] - yPredicted[k|k-1].
Examine the residuals and state estimation errors, and ensure that they have a small magnitude, zero mean, and low autocorrelation.
In this example, the Unscented Kalman Filter block outputs xhat[k|k] because the Use the current measurements to improve state estimates parameter of the block is selected. If you clear this parameter, the block instead outputs xhat[k|k-1], the predicted state value at time step k, using yMeasured until time k-1. In this case, compute yPredicted[k|k-1] = MeasurementFcn(xhat[k|k-1]), where MeasurementFcn is the measurement function for your system.
See Also
Kalman Filter | Extended Kalman Filter | Unscented Kalman Filter | Particle Filter