predint
Prediction intervals for cfit or sfit object
Syntax
Description
ci = predint(fitresult,x)cfit object fitresult at the new predictor values specified by the vector x. fitresult must be an output from the fit function to contain the necessary information for ci. ci is an n-by-2 array where n = length(x). The left column of ci contains the lower bound for each coefficient; the right column contains the upper bound.
ci = predint(fitresult,x,level,intopt,simopt)
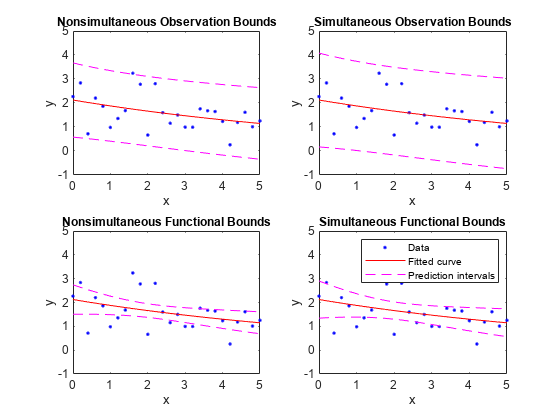
Observation bounds are wider than functional bounds because they measure the uncertainty of predicting the fitted curve plus the random variation in the new observation. Non-simultaneous bounds are for individual elements of x; simultaneous bounds are for all elements of x.
Examples
Input Arguments
Output Arguments
Limitations
Prediction intervals cannot be computed for fit objects with constraint points
specified. The software will return NaN values.
Version History
Introduced in R2013a