dsp.STFT
Short-time FFT
Description
The dsp.STFT object computes the short-time Fourier transform
(STFT) of the time-domain input signal. The object accepts frames of time-domain data, buffers
them to the desired window length and overlap length, multiplies the samples by the window,
and then performs FFT on the buffered windows. For more details, see Algorithms.
Use the STFT to analyze the frequency content of a signal that varies with time.
Creation
Syntax
Description
stf = dsp.STFTstf, that implements the short-time FFT. The object processes the
data independently across each input channel over time.
stf = dsp.STFT(window)window.
stf = dsp.STFT(window,overlap)Window property set to
window and the OverlapLength
property set to overlap.
stf = dsp.STFT(window,overlap,nfft)Window property set to
window, the OverlapLength property set to
overlap, and the FFTLength
property set to nfft.
stf = dsp.STFT(Name,Value)
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
step | Run System object algorithm |
release | Release resources and allow changes to System object property values and input characteristics |
reset | Reset internal states of System object |
clone | Create duplicate System object |
isLocked | Determine if System object is in use |
getFrequencyVector | Get the vector of frequencies at which the short-time FFT is computed |
Examples
More About
Algorithms
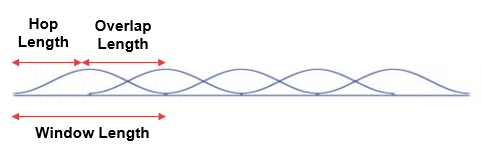
Here is a sketch of how the algorithm is implemented:

The time-domain input signal is buffered based on a user-specified window length (WL) and overlap length (OL). The hop size, R, is defined as R = WL – OL. Buffered windows are multiplied by a user-specified window of length WL. The STFT output is the FFT of this product. The number of time-domain samples required to form a new FFT output is R.
Here is an illustration of how a random signal looks like in the original time-domain, after multiplying with the overlapping windows, and after applying FFT on the multiplied windows:

References
[1] Allen, J.B., and L. R. Rabiner. "A Unified Approach to Short-Time Fourier Analysis and Synthesis,'' Proceedings of the IEEE, Vol. 65, pp. 1558–1564, Nov. 1977.
Extended Capabilities
Version History
Introduced in R2019a