iirparameq

(Removed) IIR biquad digital parametric equalizer filter

The iirparameq function has been removed. Use the designParamEQ (Audio Toolbox) function instead. For more information on how to update your existing code, see Version History.

Syntax

[SOS,SV] = iirparameq(N,G,Wo,BW)

[SOS,SV,B,A] = iirparameq(N,G,Wo,BW)

Description

[SOS,SV] = iirparameq(N,G,Wo,BW) returns the coefficients of an Nth order IIR biquad digital parametric equalizer with gain G, center frequency Wo, and bandwidth BW. The coefficients are returned in a second-order section matrix, SOS, and a vector of scale values between each biquad stage, SV.

[SOS,SV,B,A] = iirparameq(N,G,Wo,BW) additionally returns a matrix of numerator fourth-order sections, B, and a matrix A of denominator fourth-order sections, A. These can be used in lieu of a biquad implementation and are useful for the case Wo = 0.5.

Examples

Second-order section matrices of the parametric equalizer

Compute the second-order section matrix and scale values of a parametric equalizer.

[SOS,SV] = iirparameq(6,5,0.0042,0.0028)

SOS =

    1.0000   -1.9892    0.9894    1.0000   -1.9911    0.9912
    1.0000   -1.9926    0.9929    1.0000   -1.9941    0.9944
    1.0000   -1.9964    0.9965    1.0000   -1.9967    0.9968

SV =

    1.0009
    1.0000
    1.0009
    1.0000

Fourth-order section matrices of the parametric equalizer

Compute the numerator and denominator coefficients of the fourth-order sections of the parametric equalizer.

[SOS,SV,B,A] = iirparameq(6,5,0.0042,0.0028)

SOS =

    1.0000   -1.9892    0.9894    1.0000   -1.9911    0.9912
    1.0000   -1.9926    0.9929    1.0000   -1.9941    0.9944
    1.0000   -1.9964    0.9965    1.0000   -1.9967    0.9968

SV =

    1.0009
    1.0000
    1.0009
    1.0000

B =

    1.0009   -1.9911    0.9903         0         0
    1.0009   -3.9927    5.9729   -3.9715    0.9903

A =

    1.0000   -1.9911    0.9912         0         0
    1.0000   -3.9908    5.9729   -3.9733    0.9912

Two Equalizers Centered at Different Frequencies

Design two equalizers centered at 100 Hz and 1000 Hz respectively, both with a gain of 5 dB and a Q-factor of 1.5, for a system running at 48 kHz.

Fs  = 48e3;
N   = 6;
G   = 5;
Q   = 1.5;
Wo1 = 100/(Fs/2);
Wo2 = 1000/(Fs/2);
% Obtain the bandwidth of the equalizers from the center frequencies and
% Q-factors.
BW1 = Wo1/Q;
BW2 = Wo2/Q;
% Design the equalizers and obtain their SOS and SV values.
[SOS1,SV1] = iirparameq(N,G,Wo1,BW1);  
[SOS2,SV2] = iirparameq(N,G,Wo2,BW2);

Design biquad filters using the obtained SOS and SV values.

BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1);
BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2,'ScaleValues',SV2);

Plot the magnitude response of both filters using a log scale.

fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log');
legend('Equalizer centered at 100 Hz','Equalizer centered at 1000 Hz');

Compare Notch Filters Designed with Different Orders

Design an eighth-order notch filter and compare it to a traditional second-order notch filter designed with IIRNOTCH.

Fs  = 44.1e3;
N   = 8;
G   = -inf;
Q   = 1.8;
Wo  = 60/(Fs/2); % Notch at 60 Hz
BW  = Wo/Q; % Bandwidth occurs at -3 dB for this special case
[SOS1,SV1] = iirparameq(N,G,Wo,BW);  
[NUM,DEN]  = iirnotch(Wo,BW); 
SOS2 = [NUM,DEN];

Design the notch filters using the SOS and SV values.

BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1);
BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2);

Plot the magnitude response of both filters. The filters intersect at -3 dB point.

FVT = fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log');
legend(FVT,'8th order notch filter','2nd order notch filter');

Input Arguments

N — Order of the parametric equalizer

even positive integer

Order of the parametric equalizer, specified as an even positive integer.

Example: 6

Example: 10

Data Types: single | double

G — Gain of the parametric equalizer

real scalar

Gain of the parametric equalizer in dB, specified as a real scalar.

Example: 2

Example: -2.2

Data Types: single | double

Wo — Center frequency of the parametric equalizer

real scalar

Center frequency of the parametric equalizer, specified as a real scalar in the range [0.0 1.0]. A value of 1.0 corresponds to π radians/sample.

Example: 0.0

Example: 1.0

Data Types: single | double

BW — Bandwidth of the parametric equalizer

real scalar

Bandwidth of the parametric equalizer, specified as a real scalar in the range [0.0 1.0]. A value of 1.0 corresponds to π radians/sample.

Example: 0.0

Example: 1.0

Data Types: single | double

Output Arguments

SOS — Second-order section matrix

real-valued matrix

Second-order section matrix, returned as a real-valued L-by-6 matrix, where L is the number of second-order sections of the filter.

SV — Scale values between each biquad stage

real-valued vector

Scale values between each biquad stage, returned as a real-valued vector of length L + 1.

B — Numerator coefficients of the fourth-order sections of the parametric equalizer

real-valued matrix

Numerator coefficients of the fourth-order sections of the parametric equalizer, returned as a real-valued M-by-5 matrix. M is the number of fourth-order sections of the filter.

A — Denominator coefficients of the fourth-order sections of the parametric equalizer

real-valued matrix

Denominator coefficients of the fourth-order sections of the parametric equalizer, returned as a real-valued M-by-5 matrix. M is the number of fourth-order sections of the filter.

Algorithms

High-order Parametric Equalizer

Parametric equalizers are digital filters used in audio processing for adjusting the frequency content of a sound signal. Parametric equalizers provide capabilities beyond those of graphic equalizers by allowing the adjustment of gain, center frequency, and bandwidth of each filter. In contrast, graphic equalizers allow for the adjustment of the gain of each filter only. Digital parametric audio equalizers are commonly implemented as biquadratic (second-order IIR) filters. Due to low order, biquadratic filters can present relatively large ripple or transition regions. When several filters are connected in cascade, they can overlap with each other. In such circumstances, high-order filters are preferred. High-order filters provide flatter passbands, sharper band edges, and more control over the shape of each filter. In addition, if the order of the filter is set to two, the design changes to a special case: a traditional second-order parametric equalizer.

The figure shows the magnitude response of a second-order parametric equalizer compared with a high-order parametric equalizer.

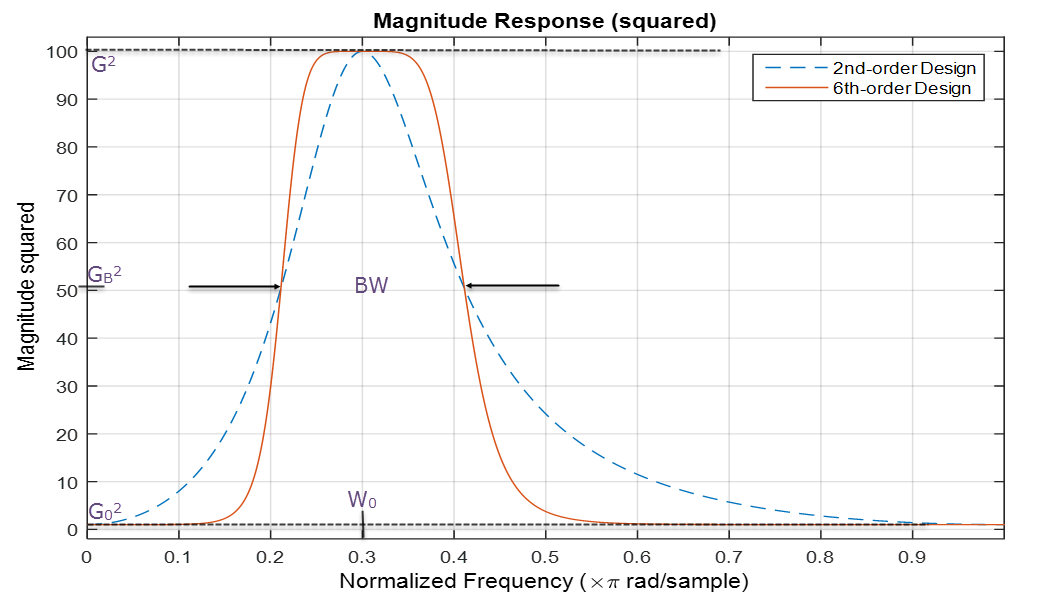
W₀ = 0.3 × π radians/sample is the center frequency of the equalizer, BW = 0.2 radians/sample is the bandwidth of the equalizer, G = 10 is the peak gain of the equalizer, G₀ = 1, and G_B = (G₀² + G²) / 2.

Algorithm

The first step in the filter design is to design a high-order analog lowpass shelving filter that meets the specified gain and bandwidth. A high-order Butterworth filter is used for this purpose. The analog Butterworth filter is then transformed into a digital lowpass shelving filter, and finally into a peaking equalizer that is centered at the specified peak frequency.

The design specifications for the digital equalizer are the order of the equalizer, N, the gain of the equalizer, G, the center frequency of the equalizer, W₀, and the bandwidth of the equalizer, BW.

The transfer function of the high-order parametric equalizer is given by:

$$H(z)={[\frac{b_{00}+b_{01}{z}^{-1}+b_{02}{z}^{-2}}{1+a_{01}{z}^{-1}+a_{02}{z}^{-2}}]}^r\times {\displaystyle \prod _{i=1}^L[\frac{b_{i0}+b_{i1}{z}^{-1}+b_{i2}{z}^{-2}+b_{i3}{z}^{-3}+b_{i4}{z}^{-4}}{1+a_{i1}{z}^{-1}+a_{i2}{z}^{-2}+a_{i3}{z}^{-3}+a_{i4}{z}^{-4}}]}$$

where b₀₀, b₀₁, b₀₂, a₀₁, and a₀₂ are coefficients of the second-order section of the equalizer. b_i0, b_i1, b_i2, b_i3, b_i4, a_i1, a_i2, and a_i3 are coefficients of the fourth-order sections of the equalizer. L = (N –r) / 2, where r = 1 when N is odd, and r = 0 when N is even. The fourth-order sections are factored into second-order sections so that you can implement them using biquad filters.

For more information on how coefficients are computed in terms of the design specifications, see the "Butterworth Designs" section in [1].

References

[1] Sophocles J. Orphanidis. "High-Order Digital Parametric Equalizer Design." J. Audio Eng. Soc. Vol. 53, November 2005, pp. 1026–1046.

Version History

Introduced in R2015a

R2023b: iirparameq has been removed

The iirparameq function has been removed. Use the designParamEQ (Audio Toolbox) function instead.

Update Code

This table shows how the function is typically used and explains how to update the existing code to use the designParamEQ function.

Discouraged Usage	Recommended Replacement
Design based on filter bandwidth Fs = 48e3; N = 2; Q = 10; G = 9; % 9 dB % Normalized center frequency Wo1 = 2000/(Fs/2); Wo2 = 12000/(Fs/2); % Normalized bandwidth BW1 = Wo1/Q; BW2 = Wo2/Q; [SOS1,SV1] = iirparameq(N,G,Wo1,BW1); [SOS2,SV2] = iirparameq(N,G,Wo2,BW2); BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1); BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2,'ScaleValues',SV2); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log'); legend(hfvt,'BW1 = 200 Hz; Q = 10','BW2 = 1200 Hz; Q = 10');	Design based on filter bandwidth Fs = 48e3; N = 2; Q = 10; G = 9; % 9 dB % Normalized center frequency Wo1 = 2000/(Fs/2); Wo2 = 12000/(Fs/2); % Normalized bandwidth BW1 = Wo1/Q; BW2 = Wo2/Q; [B1,A1] = designParamEQ(N,G,Wo1,BW1); [B2,A2] = designParamEQ(N,G,Wo2,BW2); BQ1 = dsp.BiquadFilter('SOSMatrix',[B1.',[1,A1.']]); BQ2 = dsp.BiquadFilter('SOSMatrix',[B2.',[1,A2.']]); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log'); legend(hfvt,'BW1 = 200 Hz; Q = 10','BW2 = 1200 Hz; Q = 10');
Design based on quality factor Fs = 48e3; N = 2; G = 15; % 15 dB % Quality factor Q1 = 0.48; Q2 = 1/sqrt(2); % Normalized center frequency Wo = 6000/(Fs/2); % Normalized bandwidth BW1 = Wo/Q1; BW2 = Wo/Q2; [SOS1,SV1] = iirparameq(N,G,Wo,BW1); [SOS2,SV2] = iirparameq(N,G,Wo,BW2); BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1); BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2,'ScaleValues',SV2); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'Color','white'); legend(hfvt,'Q = 0.48','Q = 0.7071');	Design based on quality factor Fs = 48e3; N = 2; G = 15; % 15 dB % Quality factor Q1 = 0.48; Q2 = 1/sqrt(2); % Normalized center frequency Wo = 6000/(Fs/2); % Normalized bandwidth BW1 = Wo/Q1; BW2 = Wo/Q2; [B1,A1] = designParamEQ(N,G,Wo,BW1); [B2,A2] = designParamEQ(N,G,Wo,BW2); BQ1 = dsp.BiquadFilter('SOSMatrix',[B1.',[1,A1.']]); BQ2 = dsp.BiquadFilter('SOSMatrix',[B2.',[1,A2.']]); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'Color','white'); legend(hfvt,'Q = 0.48','Q = 0.7071');
Low shelf and high shelf filters Fs = 48e3; N = 4; G = 10; % 10 dB % Normalized center frequency Wo1 = 0; % Lowpass filter % Corresponds to Fs/2 (Hz) or pi (rad/sample) Wo2 = 1; % Highpass filter % Bandwidth occurs at 7.4 dB in this case BW = 1000/(Fs/2); [SOS1,SV1] = iirparameq(N,G,Wo1,BW); [SOS2,SV2] = iirparameq(N,G,Wo2,BW); BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1); BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2,'ScaleValues',SV2); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'Color','white'); legend(hfvt,'Low Shelf Filter','High Shelf Filter');	Low shelf and high shelf filters Fs = 48e3; N = 4; G = 10; % 10 dB % Normalized center frequency Wo1 = 0; % Lowpass filter % Corresponds to Fs/2 (Hz) or pi (rad/sample) Wo2 = 1; % Highpass filter % Bandwidth occurs at 7.4 dB in this case BW = 1000/(Fs/2); [B1,A1] = designParamEQ(N,G,Wo1,BW); [B2,A2] = designParamEQ(N,G,Wo2,BW); BQ1 = dsp.BiquadFilter('SOSMatrix',[B1.',[ones(2,1),A1.']]); BQ2 = dsp.BiquadFilter('SOSMatrix',[B2.',[ones(2,1),A2.']]); % Visualize the filters hfvt = fvtool(BQ1,BQ2,'Fs',Fs,'Color','white'); legend(hfvt,'Low Shelf Filter','High Shelf Filter');

R2022a: iirparameq will be removed

The iirparameq function will be removed in a future release. Existing instances of the function continue to run. For new code, use the designParamEQ (Audio Toolbox) function instead.