simulate
Simulate coefficients and innovations covariance matrix of Bayesian vector autoregression (VAR) model
Syntax
Description
[ returns a random vector of coefficients Coeff,Sigma]
= simulate(PriorMdl)Coeff and a random innovations covariance matrix Sigma drawn from the prior Bayesian VAR(p) model
PriorMdl.
[ specifies options using one or more name-value pair arguments in addition to any of the input argument combinations in the previous syntaxes. For example, you can set the number of random draws from the distribution or specify the presample response data.Coeff,Sigma]
= simulate(___,Name,Value)
Examples
Consider the 3-D VAR(4) model for the US inflation (INFL), unemployment (UNRATE), and federal funds (FEDFUNDS) rates.
For all , is a series of independent 3-D normal innovations with a mean of 0 and covariance . Assume that a conjugate prior distribution governs the behavior of the parameters.
Create a conjugate prior model. Specify the response series names. Obtain a summary of the prior distribution.
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; numseries = numel(seriesnames); numlags = 4; PriorMdl = bayesvarm(numseries,numlags,'ModelType','conjugate',... 'SeriesNames',seriesnames); Summary = summarize(PriorMdl,'off');
Draw a set of coefficients and an innovations covariance matrix from the prior distribution.
rng(1) % For reproducibility
[Coeff,Sigma] = simulate(PriorMdl);Display the selected coefficients with corresponding names and the innovations covariance matrix.
table(Coeff,'RowNames',Summary.CoeffMap)ans=39×1 table
Coeff
__________
AR{1}(1,1) 0.44999
AR{1}(1,2) 0.047463
AR{1}(1,3) -0.042106
AR{2}(1,1) -0.0086264
AR{2}(1,2) 0.034049
AR{2}(1,3) -0.058092
AR{3}(1,1) -0.015698
AR{3}(1,2) -0.053203
AR{3}(1,3) -0.031138
AR{4}(1,1) 0.036431
AR{4}(1,2) -0.058279
AR{4}(1,3) -0.02195
Constant(1) -1.001
AR{1}(2,1) -0.068182
AR{1}(2,2) 0.51029
AR{1}(2,3) -0.094367
⋮
AR{r}(j,k) is the AR coefficient of response variable k (lagged r units) in response equation j.
Sigma
Sigma = 3×3
0.1238 -0.0053 -0.0369
-0.0053 0.0456 0.0160
-0.0369 0.0160 0.1039
Rows and columns of Sigma correspond to the innovations in the response equations ordered by PriorMdl.SeriesNames.
Consider the 3-D VAR(4) model of Draw Coefficients and Innovations Covariance Matrix from Prior Distribution. In this case, assume that the prior distribution is diffuse.
Load and Preprocess Data
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values.
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create Prior Model
Create a diffuse Bayesian VAR(4) prior model for the three response series. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = bayesvarm(numseries,numlags,'SeriesNames',seriesnames);Estimate Posterior Distribution
Estimate the posterior distribution. Return the estimation summary.
[PosteriorMdl,Summary] = estimate(PriorMdl,rmDataTimeTable{:,seriesnames});Bayesian VAR under diffuse priors
Effective Sample Size: 197
Number of equations: 3
Number of estimated Parameters: 39
| Mean Std
-------------------------------
Constant(1) | 0.1007 0.0832
Constant(2) | -0.0499 0.0450
Constant(3) | -0.4221 0.1781
AR{1}(1,1) | 0.1241 0.0762
AR{1}(2,1) | -0.0219 0.0413
AR{1}(3,1) | -0.1586 0.1632
AR{1}(1,2) | -0.4809 0.1536
AR{1}(2,2) | 0.4716 0.0831
AR{1}(3,2) | -1.4368 0.3287
AR{1}(1,3) | 0.1005 0.0390
AR{1}(2,3) | 0.0391 0.0211
AR{1}(3,3) | -0.2905 0.0835
AR{2}(1,1) | 0.3236 0.0868
AR{2}(2,1) | 0.0913 0.0469
AR{2}(3,1) | 0.3403 0.1857
AR{2}(1,2) | -0.0503 0.1647
AR{2}(2,2) | 0.2414 0.0891
AR{2}(3,2) | -0.2968 0.3526
AR{2}(1,3) | 0.0450 0.0413
AR{2}(2,3) | 0.0536 0.0223
AR{2}(3,3) | -0.3117 0.0883
AR{3}(1,1) | 0.4272 0.0860
AR{3}(2,1) | -0.0389 0.0465
AR{3}(3,1) | 0.2848 0.1841
AR{3}(1,2) | 0.2738 0.1620
AR{3}(2,2) | 0.0552 0.0876
AR{3}(3,2) | -0.7401 0.3466
AR{3}(1,3) | 0.0523 0.0428
AR{3}(2,3) | 0.0008 0.0232
AR{3}(3,3) | 0.0028 0.0917
AR{4}(1,1) | 0.0167 0.0901
AR{4}(2,1) | 0.0285 0.0488
AR{4}(3,1) | -0.0690 0.1928
AR{4}(1,2) | -0.1830 0.1520
AR{4}(2,2) | -0.1795 0.0822
AR{4}(3,2) | 0.1494 0.3253
AR{4}(1,3) | 0.0067 0.0395
AR{4}(2,3) | 0.0088 0.0214
AR{4}(3,3) | -0.1372 0.0845
Innovations Covariance Matrix
| INFL DUNRATE DFEDFUNDS
-------------------------------------------
INFL | 0.3028 -0.0217 0.1579
| (0.0321) (0.0124) (0.0499)
DUNRATE | -0.0217 0.0887 -0.1435
| (0.0124) (0.0094) (0.0283)
DFEDFUNDS | 0.1579 -0.1435 1.3872
| (0.0499) (0.0283) (0.1470)
PosteriorMdl is a conjugatebvarm model, which is analytically tractable.
Simulate Parameters from Posterior
Draw 1000 samples from the posterior distribution.
rng(1)
[Coeff,Sigma] = simulate(PosteriorMdl,'NumDraws',1000);Coeff is a 39-by-1000 matrix of randomly drawn coefficients. Each column is an individual draw, and each row is an individual coefficient. Sigma is a 3-by-3-by-1000 array of randomly drawn innovations covariance matrices. Each page is an individual draw.
Display the first coefficient drawn from the distribution with corresponding parameter names, and display the first drawn innovations covariance matrix.
Coeffs = table(Coeff(:,1),'RowNames',Summary.CoeffMap)Coeffs=39×1 table
Var1
_________
AR{1}(1,1) 0.14994
AR{1}(1,2) -0.46927
AR{1}(1,3) 0.088388
AR{2}(1,1) 0.28139
AR{2}(1,2) -0.19597
AR{2}(1,3) 0.049222
AR{3}(1,1) 0.3946
AR{3}(1,2) 0.081871
AR{3}(1,3) 0.002117
AR{4}(1,1) 0.13514
AR{4}(1,2) -0.23661
AR{4}(1,3) -0.01869
Constant(1) 0.035787
AR{1}(2,1) 0.0027895
AR{1}(2,2) 0.62382
AR{1}(2,3) 0.053232
⋮
Sigma(:,:,1)
ans = 3×3
0.2653 -0.0075 0.1483
-0.0075 0.1015 -0.1435
0.1483 -0.1435 1.5042
Consider the 3-D VAR(4) model of Draw Coefficients and Innovations Covariance Matrix from Prior Distribution. In this case, assume that the prior distribution is semiconjugate.
Load and Preprocess Data
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values.
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create Prior Model
Create a semiconjugate Bayesian VAR(4) prior model for the three response series. Specify the response variable names.
numseries = numel(seriesnames); numlags = 4; PriorMdl = bayesvarm(numseries,numlags,'Model','semiconjugate',... 'SeriesNames',seriesnames);
Simulate Parameters from Posterior
Because the joint posterior distribution of a semiconjugate prior model is analytically intractable, simulate sequentially draws from the full conditional distributions.
Draw 1000 samples from the posterior distribution. Specify a burn-in period of 10,000, and a thinning factor of 5. Start the Gibbs sampler by assuming the posterior mean of is the 3-D identity matrix.
rng(1)
[Coeff,Sigma] = simulate(PriorMdl,rmDataTimeTable{:,seriesnames},...
'NumDraws',1000,'BurnIn',1e4,'Thin',5,'Sigma0',eye(3));Coeff is a 39-by-1000 matrix of randomly drawn coefficients. Each column is an individual draw, and each row is an individual coefficient. Sigma is a 3-by-3-by-1000 array of randomly drawn innovations covariance matrices. Each page is an individual draw.
Consider the 2-D VARX(1) model for the US real GDP (RGDP) and investment (GCE) rates that treats the personal consumption (PCEC) rate as exogenous:
For all , is a series of independent 2-D normal innovations with a mean of 0 and covariance . Assume the following prior distributions:
, where M is a 4-by-2 matrix of means and is the 4-by-4 among-coefficient scale matrix. Equivalently, .
where Ω is the 2-by-2 scale matrix and is the degrees of freedom.
Load the US macroeconomic data set. Compute the real GDP, investment, and personal consumption rate series. Remove all missing values from the resulting series.
load Data_USEconModel DataTimeTable.RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF; seriesnames = ["PCEC"; "RGDP"; "GCE"]; rates = varfun(@price2ret,DataTimeTable,'InputVariables',seriesnames); rates = rmmissing(rates); rates.Properties.VariableNames = seriesnames;
Create a conjugate prior model for the 2-D VARX(1) model parameters.
numseries = 2; numlags = 1; numpredictors = 1; PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,... 'SeriesNames',seriesnames(2:end));
Simulate directly from the posterior distribution. Specify the exogenous predictor data.
[Coeff,Sigma] = simulate(PriorMdl,rates{:,PriorMdl.SeriesNames},...
'X',rates{:,seriesnames(1)});By default, simulate uses the first p = 1 observations of the response data to initialize the dynamic component of the model, and removes the corresponding observations from the predictor data.
Input Arguments
Prior Bayesian VAR model, specified as a model object in this table.
| Model Object | Description |
|---|---|
conjugatebvarm | Dependent, matrix-normal-inverse-Wishart conjugate model returned by bayesvarm or conjugatebvarm |
semiconjugatebvarm | Independent, normal-inverse-Wishart semiconjugate prior model returned by bayesvarm or semiconjugatebvarm |
diffusebvarm | Diffuse prior model returned by bayesvarm or diffusebvarm |
normalbvarm | Normal conjugate model with a fixed innovations covariance matrix, returned by bayesvarm or normalbvarm |
Observed multivariate response series to which simulate fits the model, specified as a numobs-by-numseries numeric matrix.
numobs is the sample size. numseries is the number of response variables (PriorMdl.NumSeries).
Rows correspond to observations, and the last row contains the latest observation. Columns correspond to individual response variables.
Y represents the continuation of the presample response series in Y0.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Y0',Y0,'X',X specifies the presample response data Y0 to initialize the VAR model for posterior estimation, and the predictor data X for the exogenous regression component.
Options for All Prior Distributions
Number of random draws from the distributions, specified as the comma-separated pair consisting of 'NumDraws' and a positive integer.
Example: 'NumDraws',1e7
Data Types: double
Presample response data to initialize the VAR model for estimation, specified as the comma-separated pair consisting of 'Y0' and a numpreobs-by-numseries numeric matrix. numpreobs is the number of presample observations.
Rows correspond to presample observations, and the last row contains the latest observation. Y0 must have at least PriorMdl.P rows. If you supply more rows than necessary, simulate uses the latest PriorMdl.P observations only.
Columns must correspond to the response series in Y.
By default, simulate uses Y(1:PriorMdl.P,:) as presample observations, and then estimates the posterior using Y((PriorMdl.P + 1):end,:). This action reduces the effective sample size.
Data Types: double
Predictor data for the exogenous regression component in the model, specified as the comma-separated pair consisting of 'X' and a numobs-by-PriorMdl.NumPredictors numeric matrix.
Rows correspond to observations, and the last row contains the latest observation. simulate does not use the regression component in the presample period. X must have at least as many observations as the observations used after the presample period.
In either case, if you supply more rows than necessary, simulate uses the latest observations only.
Columns correspond to individual predictor variables. All predictor variables are present in the regression component of each response equation.
Data Types: double
Options for Semiconjugate Prior Distributions
Number of draws to remove from the beginning of the sample to reduce transient effects, specified as the comma-separated pair consisting of 'BurnIn' and a nonnegative scalar. For details on how simulate reduces the full sample, see Algorithms.
Tip
To help you specify the appropriate burn-in period size:
Determine the extent of the transient behavior in the sample by setting the
BurnInname-value argument to0.Simulate a few thousand observations by using
simulate.Create trace plots.
Example: 'BurnIn',0
Data Types: double
Adjusted sample size multiplier, specified as the comma-separated pair consisting of 'Thin' and a positive integer.
The actual sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, simulate discards every Thin – 1 draws, and then retains the next draw. For more details on how simulate reduces the full sample, see Algorithms.
Tip
To reduce potential large serial correlation in the sample, or to reduce the memory consumption of the draws stored in Coeff and Sigma, specify a large value for Thin.
Example: 'Thin',5
Data Types: double
Starting value of the VAR model coefficients for the Gibbs sampler, specified as the comma-separated pair consisting of 'Coeff0' and a numeric column vector with (PriorMdl.NumSeries*)-by-kNumDraws elements, where k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictorsCoeff0, see the output Coeff.
By default, Coeff0 is the multivariate least-squares estimate.
Tip
To specify
Coeff0:Set separate variables for the initial values each coefficient matrix and vector.
Horizontally concatenate all coefficient means in this order:
Vectorize the transpose of the coefficient mean matrix.
Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
A good practice is to run
simulatemultiple times with different parameter starting values. Verify that the estimates from each run converge to similar values.
Data Types: double
Starting value of the innovations covariance matrix for the Gibbs sampler, specified as the comma-separated pair consisting of 'Sigma0' and a PriorMdl.NumSeries-by-PriorMdl.NumSeries positive definite numeric matrix. By default, Sigma0 is the residual mean squared error from multivariate least-squares. Rows and columns correspond to innovations in the equations of the response variables ordered by PriorMdl.SeriesNames.
Tip
A good practice is to run simulate multiple times with different parameter starting values. Verify that the estimates from each run converge to similar values.
Data Types: double
Output Arguments
Simulated VAR model coefficients, returned as a (PriorMdl.NumSeries*)-by-kNumDraws numeric matrix, where k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors
For draw jCoeff(1: corresponds to all coefficients in the equation of response variable k,j)PriorMdl.SeriesNames(1), Coeff(( corresponds to all coefficients in the equation of response variable k + 1):(2*k),j)PriorMdl.SeriesNames(2), and so on. For a set of indices corresponding to an equation:
Elements
1throughPriorMdl.NumSeriescorrespond to the lag 1 AR coefficients of the response variables ordered byPriorMdl.SeriesNames.Elements
PriorMdl.NumSeries + 1through2*PriorMdl.NumSeriescorrespond to the lag 2 AR coefficients of the response variables ordered byPriorMdl.SeriesNames.In general, elements
(throughq– 1)*PriorMdl.NumSeries + 1q*PriorMdl.NumSeriesqPriorMdl.SeriesNames.If
PriorMdl.IncludeConstantistrue, elementPriorMdl.NumSeries*PriorMdl.P + 1is the model constant.If
PriorMdl.IncludeTrendistrue, elementPriorMdl.NumSeries*PriorMdl.P + 2is the linear time trend coefficient.If
PriorMdl.NumPredictors> 0, elementsPriorMdl.NumSeries*PriorMdl.P + 3throughk
This figure shows the structure of Coeff(L, for a 2-D VAR(3) model that contains a constant vector and four exogenous predictors.j)
where
ϕq,jk is element (j,k) of the lag q AR coefficient matrix.
cj is the model constant in the equation of response variable j.
Bju is the regression coefficient of exogenous variable u in the equation of response variable j.
Simulated innovations covariance matrices, returned as a PriorMdl.NumSeries-by-PriorMdl.NumSeries-by-NumDraws array of positive definite numeric matrices.
Each page is a separate draw (covariance) from the distribution. Rows and columns correspond to innovations in the equations of the response variables ordered by PriorMdl.SeriesNames.
If PriorMdl is a normalbvarm object, all covariances in Sigma are equal to PriorMdl.Covariance.
Limitations
simulatecannot draw values from an improper distribution, which is a distribution whose density does not integrate to 1.
More About
A Bayesian VAR model treats all coefficients and the innovations covariance matrix as random variables in the m-dimensional, stationary VARX(p) model. The model has one of the three forms described in this table.
| Model | Equation |
|---|---|
| Reduced-form VAR(p) in difference-equation notation |
|
| Multivariate regression |
|
| Matrix regression |
|
For each time t = 1,...,T:
yt is the m-dimensional observed response vector, where m =
numseries.Φ1,…,Φp are the m-by-m AR coefficient matrices of lags 1 through p, where p =
numlags.c is the m-by-1 vector of model constants if
IncludeConstantistrue.δ is the m-by-1 vector of linear time trend coefficients if
IncludeTrendistrue.Β is the m-by-r matrix of regression coefficients of the r-by-1 vector of observed exogenous predictors xt, where r =
NumPredictors. All predictor variables appear in each equation.which is a 1-by-(mp + r + 2) vector, and Zt is the m-by-m(mp + r + 2) block diagonal matrix
where 0z is a 1-by-(mp + r + 2) vector of zeros.
, which is an (mp + r + 2)-by-m random matrix of the coefficients, and the m(mp + r + 2)-by-1 vector λ = vec(Λ).
εt is an m-by-1 vector of random, serially uncorrelated, multivariate normal innovations with the zero vector for the mean and the m-by-m matrix Σ for the covariance. This assumption implies that the data likelihood is
where f is the m-dimensional multivariate normal density with mean ztΛ and covariance Σ, evaluated at yt.
Before considering the data, you impose a joint prior distribution assumption on (Λ,Σ), which is governed by the distribution π(Λ,Σ). In a Bayesian analysis, the distribution of the parameters is updated with information about the parameters obtained from the data likelihood. The result is the joint posterior distribution π(Λ,Σ|Y,X,Y0), where:
Y is a T-by-m matrix containing the entire response series {yt}, t = 1,…,T.
X is a T-by-m matrix containing the entire exogenous series {xt}, t = 1,…,T.
Y0 is a p-by-m matrix of presample data used to initialize the VAR model for estimation.
Tips
Monte Carlo simulation is subject to variation. If
simulateuses Monte Carlo simulation, then estimates and inferences might vary when you callsimulatemultiple times under seemingly equivalent conditions. To reproduce estimation results, set a random number seed by usingrngbefore callingsimulate.
Algorithms
If
simulateestimates a posterior distribution (when you supplyY) and the posterior is analytically tractable,simulatesimulates directly from the posterior. Otherwise,simulateuses the Gibbs sampler to estimate the posterior.This figure shows how
simulatereduces the sample by using the values ofNumDraws,Thin, andBurnIn. Rectangles represent successive draws from the distribution.simulateremoves the white rectangles from the sample. The remainingNumDrawsblack rectangles compose the sample.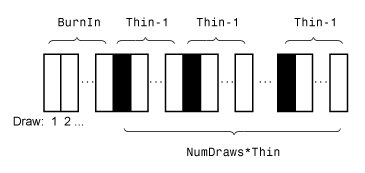
If
PriorMdlis asemiconjugatebvarmobject and you do not specify starting values (Coeff0andSigma0),simulatesamples from the posterior distribution by applying the Gibbs sampler.simulateuses the default value ofSigma0for Σ and draws a value of Λ from π(Λ|Σ,Y,X), the full conditional distribution of the VAR model coefficients.simulatedraws a value of Σ from π(Σ|Λ,Y,X), the full conditional distribution of the innovations covariance matrix, by using the previously generated value of Λ.The function repeats steps 1 and 2 until convergence. To assess convergence, draw a trace plot of the sample.
If you specify
Coeff0,simulatedraws a value of Σ from π(Σ|Λ,Y,X) to start the Gibbs sampler.simulatedoes not return default starting values that it generates.
Version History
Introduced in R2020a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)