Share Results of Econometric Modeler App Session
This example shows how to share the results of an Econometric Modeler app session by:
Exporting time series and model variables to the MATLAB® Workspace
Generating MATLAB plain text and live functions to use outside the app
Generating a report of your activities on time series and estimated models
During the session, the example transforms and plots data, runs
statistical tests, and estimates a multiplicative seasonal ARIMA model. The data set Data_Airline.mat contains monthly counts of airline passengers.
Import Data into Econometric Modeler
At the command line, load the Data_Airline.mat data set.
load Data_AirlineAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variable PSSG appears in the Time
Series pane, its value appears in the
Preview pane, and its time series plot appears in the
Time Series Plot(PSSG) figure window.
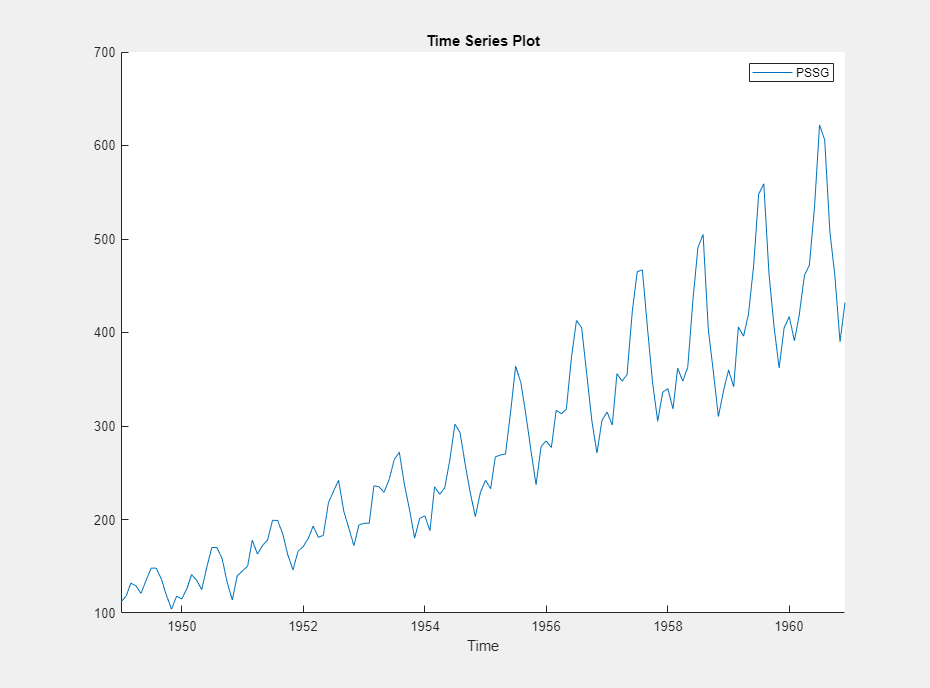
The series exhibits a seasonal trend, serial correlation, and possible exponential growth. For an interactive analysis of serial correlation, see Detect Serial Correlation Using Econometric Modeler App.
Stabilize Series
Address the exponential trend by applying the log transform to
PSSG.
In the Time Series pane, select
PSSG.On the Econometric Modeler tab, in the Transforms section, click Log.
The transformed variable PSSGLog
appears in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLog) figure
window.
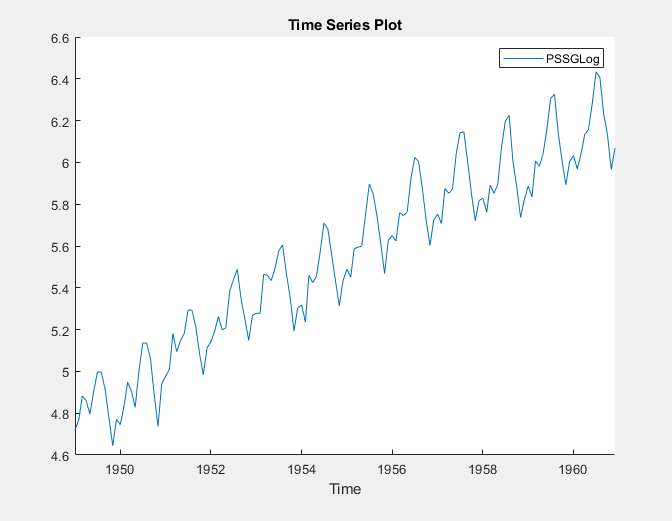
The exponential growth appears to be removed from the series.
Address the seasonal trend by applying the 12th order seasonal difference.
With PSSGLog selected in the Time
Series pane, on the Econometric Modeler tab,
in the Transforms section, set
Seasonal to 12. Then, click
Seasonal.
The transformed variable PSSGLogSeasonalDiff
appears in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLogSeasonalDiff) figure
window.

The transformed series appears to have a unit root.
Test the null hypothesis that PSSGLogSeasonalDiff
has a unit root by using the Augmented Dickey-Fuller test. Specify that the
alternative is an AR(0) model, then test again specifying an AR(1) model. Adjust
the significance level to 0.025 to maintain a total significance level of 0.05.
With
PSSGLogSeasonalDiffselected in the Time Series pane, on the Econometric Modeler tab, in the Tests section, click New Test > Augmented Dickey-Fuller Test.On the ADF tab, in the Parameters section, set Significance Level to
0.025.In the Tests section, click Run Test.
In the Parameters section, set Number of Lags to
1.In the Tests section, click Run Test.
The test results appear in the Results table of the ADF(PSSGLogSeasonalDiff) document.

Both tests fail to reject the null hypothesis that the series is a unit root process.
Address the unit root by applying the first difference to
PSSGLogSeasonalDiff. With
PSSGLogSeasonalDiff selected in the
Time Series pane, click the Econometric
Modeler tab. Then, in the Transforms
section, click Difference.
The transformed variable PSSGLogSeasonalDiffDiff
appears in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLogSeasonalDiffDiff)
figure window.
In the Time Series pane, rename the
PSSGLogSeasonalDiffDiff variable by clicking it
twice to select its name and PSSGStable.
The app updates the names of all documents associated with the transformed series.

Identify Model for Series
Determine the lag structure for a conditional mean model of the data by plotting the sample autocorrelation function (ACF) and partial autocorrelation function (PACF).
With
PSSGStableselected in the Time Series pane, click the Plots tab, then click ACF.Show the first 50 lags of the ACF. On the ACF tab, set Number of Lags to
50.Click the Plots tab, then click PACF.
Show the first 50 lags of the PACF. On the PACF tab, set Number of Lags to
50.Drag the ACF(PSSGStable) figure window above the PACF(PSSGStable) figure window.

According to [1], the
autocorrelations in the ACF and PACF suggest that the following
SARIMA(0,1,1)×(0,1,1)12 model is appropriate for
PSSGLog.
Close all figure windows.
Specify and Estimate SARIMA Model
Specify the SARIMA(0,1,1)×(0,1,1)12 model.
In the Time Series pane, select the
PSSGLogtime series.On the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.
In the models gallery, in the ARMA/ARIMA Models section, click SARIMA.
In the SARIMA Model Parameters dialog box, on the Lag Order tab:
Nonseasonal section
Set Degrees of Integration to
1.Set Moving Average Order to
1.Clear the Include Constant Term check box.
Seasonal section
Set Period to
12to indicate monthly data.Set Moving Average Order to
1.Select the Include Seasonal Difference check box.

Click Estimate.
The model variable SARIMA_PSSGLog appears in the
Models pane, its value appears in the
Preview pane, and its estimation summary appears in the
Model Summary(SARIMA_PSSGLog) document.

Export Variables to Workspace
Export PSSGLog,
PSSGStable, and
SARIMA_PSSGLog to the MATLAB Workspace.
On the Econometric Modeler tab, in the Export section, click
 .
.In the Export Variables dialog box, select the Select check boxes for the
PSSGLogandPSSGStabletime series, and theSARIMA_PSSGLogmodel (if necessary). The app automatically selects the check boxes for all variables that are highlighted in the Time Series and Models panes.
Click Export.
At the command line, list all variables in the workspace.
whos
Name Size Bytes Class Attributes Data 144x1 1152 double DataTable 144x2 3525 table DataTimeTable 144x1 3311 timetable Description 22x54 2376 char PSSGLog 144x1 1152 double PSSGStable 144x1 1152 double SARIMA_PSSGLog 1x1 7963 arima dates 144x1 1152 double series 1x1 162 cell
The contents of Data_Airline.mat, the numeric vectors
PSSGLog and PSSGStable, and the
estimated arima model object
SARIMA_PSSGLog are variables in the workspace.
Forecast the next three years (36 months) of log airline passenger counts
using SARIMA_PSSGLog. Specify the PSSGLog
as presample
data.
numObs = 36;
fPSSG = forecast(SARIMA_PSSGLog,numObs,'Y0',PSSGLog);Plot the passenger counts and the forecasts.
fh = DataTimeTable.Time(end) + calmonths(1:numObs); figure; plot(DataTimeTable.Time,exp(PSSGLog)); hold on plot(fh,exp(fPSSG)); legend('Airline Passenger Counts','Forecasted Counts',... 'Location','best') title('Monthly Airline Passenger Counts, 1949-1963') ylabel('Passenger counts') hold off

Generate Plain Text Function from App Session
Generate a MATLAB function for use outside the app. The function returns the
estimated model SARIMA_PSSGLog given
DataTimeTable.
In the Models pane of the app, select the
SARIMA_PSSGLogmodel.On the Econometric Modeler tab, in the Export section, click Export > Generate Function. The MATLAB Editor opens and contains a function named
modelTimeSeries. The function acceptsDataTimeTable(the variable you imported in this session), transforms data, and returns the estimated SARIMA(0,1,1)×(0,1,1)12 modelSARIMA_PSSGLog.
On the Editor tab, click Save > Save.
Save the function to your current folder by clicking Save in the Select File for Save As dialog box.
At the command line, estimate the
SARIMA(0,1,1)×(0,1,1)12 model by passing
DataTimeTable to modelTimeSeries. Name
the model SARIMA_PSSGLog2. Compare the estimated model to
SARIMA_PSSGLog.
SARIMA_PSSGLog2 = modelTimeSeries(DataTimeTable); summarize(SARIMA_PSSGLog) summarize(SARIMA_PSSGLog2)
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)
Effective Sample Size: 144
Number of Estimated Parameters: 3
LogLikelihood: 276.198
AIC: -546.397
BIC: -537.488
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN NaN
MA{1} -0.37716 0.066794 -5.6466 1.6364e-08
SMA{12} -0.57238 0.085439 -6.6992 2.0952e-11
Variance 0.0012634 0.00012395 10.193 2.1406e-24
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)
Effective Sample Size: 144
Number of Estimated Parameters: 3
LogLikelihood: 276.198
AIC: -546.397
BIC: -537.488
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN NaN
MA{1} -0.37716 0.066794 -5.6466 1.6364e-08
SMA{12} -0.57238 0.085439 -6.6992 2.0952e-11
Variance 0.0012634 0.00012395 10.193 2.1406e-24As expected, the models are identical.
Generate Live Function from App Session
Unlike a plain text function, a live function contains formatted text and equations that you can modify by using the Live Editor.
Generate a live function for use outside the app. The function returns the
estimated model SARIMA_PSSGLog given
DataTimeTable.
In the Models pane of the app, select the
SARIMA_PSSGLogmodel.On the Econometric Modeler tab, in the Export section, click Export > Generate Live Function. The Live Editor opens and contains a function named
modelTimeSeries. The function acceptsDataTimeTable(the variable you imported in this session), transforms data, and returns the estimated SARIMA(0,1,1)×(0,1,1)12 modelSARIMA_PSSGLog.To ensure the function does not shadow the M-file function, change the name of the function to
modelTimeSeriesMLX.
On the Live Editor tab, in the File section, click Save > Save.
Save the function to your current folder by clicking Save in the Select File for Save As dialog box.
At the command line, estimate the
SARIMA(0,1,1)×(0,1,1)12 model by passing
DataTimeTable to modelTimeSeriesMLX.
Name the model SARIMA_PSSGLog2. Compare the estimated model
to SARIMA_PSSGLog.
SARIMA_PSSGLog2 = modelTimeSeriesMLX(DataTimeTable); summarize(SARIMA_PSSGLog) summarize(SARIMA_PSSGLog2)
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)
Effective Sample Size: 144
Number of Estimated Parameters: 3
LogLikelihood: 276.198
AIC: -546.397
BIC: -537.488
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN
MA{1} -0.37716 0.066794 -5.6466 1.6364e-08
SMA{12} -0.57238 0.085439 -6.6992 2.0952e-11
Variance 0.0012634 0.00012395 10.193 2.1406e-24
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)
Effective Sample Size: 144
Number of Estimated Parameters: 3
LogLikelihood: 276.198
AIC: -546.397
BIC: -537.488
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN NaN
MA{1} -0.37716 0.066794 -5.6466 1.6364e-08
SMA{12} -0.57238 0.085439 -6.6992 2.0952e-11
Variance 0.0012634 0.00012395 10.193 2.1406e-24As expected, the models are identical.
Generate Report
Generate a PDF report of all your actions on the
PSSGLog and PSSGStable
time series, and the SARIMA_PSSGLog model.
On the Econometric Modeler tab, in the Export section, click Export > Generate Report.
In the Select Variables for Report dialog box, select the Select check boxes for the
PSSGLogandPSSGStabletime series, and theSARIMA_PSSGLogmodel (if necessary). The app automatically selects the check boxes for all variables that are highlighted in the Time Series and Models panes.
Click OK.
In the Select File to Write dialog box, navigate to the
C:\MyDatafolder.In the File name box, type
SARIMAReport.Click Save.
The app publishes the code required to create
PSSGLog, PSSGStable,
and SARIMA_PSSGLog in the PDF
C:\MyData\SARIMAReport.pdf. The report includes:
A title page and table of contents
Plots that include the selected time series
Descriptions of transformations applied to the selected time series
Results of statistical tests conducted on the selected time series
Estimation summaries of the selected models

References
[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.