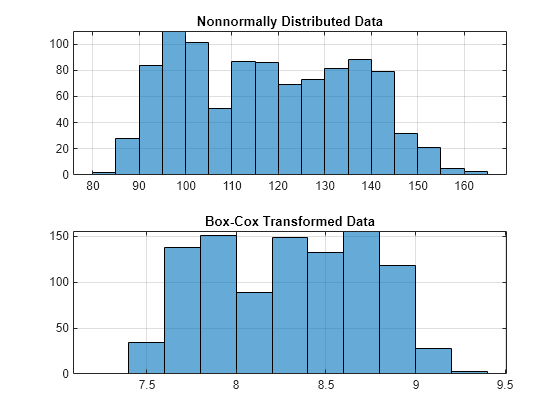
boxcox
Box-Cox transformation
Description
[
transforms the data vector transdat,lambda] = boxcox(data)data using the Box-Cox
transformation method into transdat. It also estimates the
transformation parameter λ. For more information, see Box Cox Transformation.
transdat = boxcox(lambda,data)data using a certain specified λ for the Box-Cox
transformation. This syntax does not find the optimum λ that maximizes the LLF. For
more information, see Box Cox Transformation.