optByHestonFFT
Option price by Heston model using FFT and FRFT
Syntax
Description
[
computes vanilla European option price by Heston model, using Carr-Madan FFT and Chourdakis
FRFT methods.Price,StrikeOut] = optByHestonFFT(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,V0,ThetaV,Kappa,SigmaV,RhoSV)
Note
Alternatively, you can use the Vanilla object to price
vanilla options. For more information, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.
[
adds optional name-value pair arguments. Price,StrikeOut] = optByHestonFFT(___,Name,Value)
Examples
Use optByHestonFFT to calibrate a FFT strike grid and then compute option prices and plot an option price surface.
Define Option Variables and Heston Model Parameters
AssetPrice = 80;
Rate = 0.03;
DividendYield = 0.02;
OptSpec = 'call';
V0 = 0.04;
ThetaV = 0.05;
Kappa = 1.0;
SigmaV = 0.2;
RhoSV = -0.7;Compute the Option Prices for the Entire FFT (or FRFT) Strike Grid, Without Specifying "Strike"
Compute option prices and also output the corresponding strikes. If the Strike input is empty ( [] ), option prices will be computed on the entire FFT (or FRFT) strike grid. The FFT (or FRFT) strike grid is determined as exp(log-strike grid), where each column of the log-strike grid has NumFFT points with LogStrikeStep spacing that are roughly centered around each element of log(AssetPrice). The default value for NumFFT is 2^12. In addition to the prices in the first output, the optional last output contains the corresponding strikes.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 6); Strike = []; % Strike is not specified (will use the entire FFT strike grid) % Compute option prices for the entire FFT strike grid [Call, Kout] = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield); % Show the lowest and highest strike values on the FFT strike grid format MinStrike = Kout(1) % Lowest possible strike in the current FFT strike grid
MinStrike = 2.9205e-135
MaxStrike = Kout(end) % Highest possible strike in the current FFT strike gridMaxStrike = 1.8798e+138
% Show a subset of the strikes and corresponding option prices
Range = (2046:2052);
[Kout(Range) Call(Range)]ans = 7×2
50.4929 29.4843
58.8640 21.3767
68.6231 12.5614
80.0000 4.7008
93.2631 0.6496
108.7251 0.0144
126.7505 0.0001
Change the Number of FFT (or FRFT) Points, and Compare with optByHestonNI
Try a different number of FFT (or FRFT) points, and compare the results with direct numerical integration. Unlike optByHestonFFT, which uses FFT (or FRFT) techniques for fast computation across the whole range of strikes, the optByHestonNI function uses direct numerical integration and it is typically slower, especially for multiple strikes. However, the values computed by optByHestonNI can serve as a benchmark for adjusting the settings for optByHestonFFT.
% Try a smaller number of FFT (or FRFT) points % (e.g. for faster performance or smaller memory footprint) NumFFT = 2^10; % Smaller than the default value of 2^12 Strike = []; % Strike is not specified (will use the entire FFT strike grid) [Call, Kout] = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT); % Compare with numerical integration method Range = (510:516); Strike = Kout(Range); CallFFT = Call(Range); CallNI = optByHestonNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield); Error = abs(CallFFT-CallNI); table(Strike, CallFFT, CallNI, Error)
ans=7×4 table
Strike CallFFT CallNI Error
______ _________ ___________ _________
12.696 66.066 66.696 0.62964
23.449 55.766 56.103 0.33672
43.312 36.359 36.539 0.17974
80 4.7727 4.7007 0.071928
147.76 0.066156 2.3472e-08 0.066156
272.93 0.013271 -2.5036e-09 0.013271
504.11 0.0034504 -3.0876e-07 0.0034508
Make Further Adjustments to FFT (or FRFT)
If the values in the output CallFFT are significantly different from those in CallNI, try making adjustments to optByHestonFFT settings, such as CharacteristicFcnStep, LogStrikeStep, NumFFT, DampingFactor, and so on. Note that if (LogStrikeStep * CharacteristicFcnStep) is 2*pi/ NumFFT, FFT is used. Otherwise, FRFT is used.
Strike = []; % Strike is not specified (will use the entire FFT or FRFT strike grid) [Call, Kout] = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, ... 'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001); % Compare with numerical integration method Strike = Kout(Range); CallFFT = Call(Range); CallNI = optByHestonNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield); Error = abs(CallFFT-CallNI); table(Strike, CallFFT, CallNI, Error)
ans=7×4 table
Strike CallFFT CallNI Error
______ _______ ______ __________
79.76 4.826 4.826 2.7708e-08
79.84 4.7841 4.7841 3.0111e-08
79.92 4.7423 4.7423 3.2376e-08
80 4.7007 4.7007 3.4496e-08
80.08 4.6593 4.6593 3.6457e-08
80.16 4.6181 4.6181 3.8253e-08
80.24 4.577 4.577 3.9872e-08
% Save the final FFT (or FRFT) strike grid for future reference. For % example, it provides information about the range of Strike inputs for % which the FFT (or FRFT) operation is valid. FFTStrikeGrid = Kout; MinStrike = FFTStrikeGrid(1) % Strike cannot be less than MinStrike
MinStrike = 47.9437
MaxStrike = FFTStrikeGrid(end) % Strike cannot be greater than MaxStrikeMaxStrike = 133.3566
Compute the Option Price for a Single Strike
Once the desired FFT (or FRFT) settings are determined, use the Strike input to specify the strikes rather than providing an empty array. If the specified strikes do not match a value on the FFT (or FRFT) strike grid, the outputs are interpolated on the specified strikes.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 6); Strike = 80; Call = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001)
Call = 4.7007
Compute the Option Prices for a Vector of Strikes
Use the Strike input to specify the strikes.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 6); Strike = (76:2:84)'; Call = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001)
Call = 5×1
7.0401
5.8053
4.7007
3.7316
2.8991
Compute the Option Prices for a Vector of Strikes and a Vector of Dates of the Same Lengths
Use the Strike input to specify the strikes. Also, the Maturity input can be a vector, but it must match the length of the Strike vector if the ExpandOutput name-value pair argument is not set to "true".
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, [12 18 24 30 36]); % Five maturities Strike = [76 78 80 82 84]'; % Five strikes Call = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001) % Five values in vector output
Call = 5×1
8.9560
9.3419
9.6240
9.8560
10.0500
Expand the Outputs for a Surface
Set the ExpandOutput name-value pair argument to "true" to expand the outputs into NStrikes-by NMaturities matrices. In this case, they are square matrices.
[Call, Kout] = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001, ... 'ExpandOutput', true) % (5 x 5) matrix outputs
Call = 5×5
8.9560 10.4543 11.7058 12.8009 13.7728
7.7946 9.3419 10.6337 11.7644 12.7685
6.7244 8.3028 9.6240 10.7828 11.8134
5.7475 7.3379 8.6771 9.8560 10.9074
4.8645 6.4474 7.7930 8.9840 10.0500
Kout = 5×5
76 76 76 76 76
78 78 78 78 78
80 80 80 80 80
82 82 82 82 82
84 84 84 84 84
Compute the Option Prices for a Vector of Strikes and a Vector of Dates of Different Lengths
When ExpandOutput is "true", NStrikes do not have to match NMaturities (that is, the output NStrikes-by-NMaturities matrix can be rectangular).
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12*(0.5:0.5:3)'); % Six maturities Strike = (76:2:84)'; % Five strikes Call = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001, ... 'ExpandOutput', true) % (5 x 6) matrix output
Call = 5×6
7.0401 8.9560 10.4543 11.7058 12.8009 13.7728
5.8053 7.7946 9.3419 10.6337 11.7644 12.7685
4.7007 6.7244 8.3028 9.6240 10.7828 11.8134
3.7316 5.7475 7.3379 8.6771 9.8560 10.9074
2.8991 4.8645 6.4474 7.7930 8.9840 10.0500
Compute the Option Prices for a Vector of Strikes and a Vector of Asset Prices
When ExpandOutput is "true", the output can also be a NStrikes-by-NAssetPrices rectangular matrix by accepting a vector of asset prices.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12); % Single maturity ManyAssetPrices = [70 75 80 85]; % Four asset prices Strike = (76:2:84)'; % Five strikes Call = optByHestonFFT(Rate, ManyAssetPrices, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001, ... 'ExpandOutput', true) % (5 x 4) matrix output
Call = 5×4
3.2944 5.8047 8.9560 12.6052
2.6413 4.8810 7.7946 11.2507
2.0864 4.0575 6.7244 9.9738
1.6230 3.3325 5.7475 8.7783
1.2429 2.7028 4.8645 7.6676
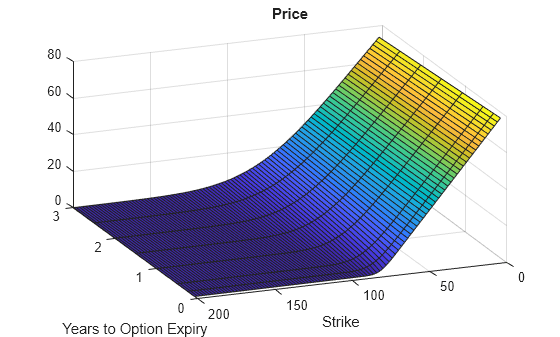
Plot an Option Price Surface
Use the Strike input to specify the strikes. Increase the value for NumFFT to support a wider range of strikes. Also, the Maturity input can be a vector. Set ExpandOutput to "true" to output the surface as a NStrikes-by-NMaturities matrix.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12*[1/12 0.25 (0.5:0.5:3)]'); Times = yearfrac(Settle, Maturity); Strike = (2:2:200)'; % Increase 'NumFFT' to support a wider range of strikes NumFFT = 2^13; Call = optByHestonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ... V0, ThetaV, Kappa, SigmaV, RhoSV, 'DividendYield', DividendYield, 'NumFFT', NumFFT, ... 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001, 'ExpandOutput', true); [X,Y] = meshgrid(Times,Strike); figure; surf(X,Y,Call); title('Price'); xlabel('Years to Option Expiry'); ylabel('Strike'); view(-112,34); xlim([0 Times(end)]); zlim([0 80]);
Input Arguments
Continuously compounded risk-free interest rate, specified as a scalar decimal value.
Data Types: double
Current underlying asset price, specified as numeric value using a scalar or a
NINST-by-1 or
NColumns-by-1 vector.
For more information on the proper dimensions for AssetPrice,
see the name-value pair argument ExpandOutput.
Data Types: double
Option settlement date, specified as a
NINST-by-1 or
NColumns-by-1 vector using a datetime array,
string array, or date character vectors. The Settle date must be
before the Maturity date.
To support existing code, optByHestonFFT also
accepts serial date numbers as inputs, but they are not recommended.
For more information on the proper dimensions for Settle, see
the name-value pair argument ExpandOutput.
Option maturity date, specified as a
NINST-by-1 or
NColumns-by-1 vector using a datetime array,
string array, or date character vectors.
To support existing code, optByHestonFFT also
accepts serial date numbers as inputs, but they are not recommended.
For more information on the proper dimensions for Maturity, see
the name-value pair argument ExpandOutput.
Definition of the option as 'call' or 'put',
specified as a NINST-by-1 or
NColumns-by-1 vector using a cell array of
character vectors or string arrays with values "call" or
"put".
For more information on the proper dimensions for OptSpec, see
the name-value pair argument ExpandOutput.
Data Types: cell | string
Option strike price value, specified as a
NINST-by-1,
NRows-by-1,
NRows-by-NColumns vector of strike
prices.
If this input is an empty array ([]), option prices are
computed on the entire FFT (or FRFT) strike grid, which is determined as
exp(log-strike grid). Each column of the log-strike grid
has 'NumFFT' points with 'LogStrikeStep' spacing
that are roughly centered around each element of log(AssetPrice).
For more information on the proper dimensions for Strike, see
the name-value pair argument ExpandOutput.
Data Types: double
Initial variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Long-term variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Mean revision speed for the underlying asset, specified as a scalar numeric value.
Data Types: double
Volatility of the variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Correlation between the Wiener processes for the underlying asset and its variance, specified as a scalar numeric value.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [Price,StrikeOut] =
optByHestonFFT(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,V0,ThetaV,Kappa,SigmaV,RhoSV,'Basis',7)
Day-count of the instrument, specified as the comma-separated pair consisting of
'Basis' and a scalar using a supported value:
0 = actual/actual
1 = 30/360 (SIA)
2 = actual/360
3 = actual/365
4 = 30/360 (PSA)
5 = 30/360 (ISDA)
6 = 30/360 (European)
7 = actual/365 (Japanese)
8 = actual/actual (ICMA)
9 = actual/360 (ICMA)
10 = actual/365 (ICMA)
11 = 30/360E (ICMA)
12 = actual/365 (ISDA)
13 = BUS/252
For more information, see Basis.
Data Types: double
Continuously compounded underlying asset yield, specified as the comma-separated
pair consisting of 'DividendYield' and a scalar numeric
value.
Data Types: double
Volatility risk premium, specified as the comma-separated pair consisting of
'VolRiskPremium' and a scalar numeric value.
Data Types: double
Flag indicating Little Heston Trap formulation by Albrecher
et
al, specified as the comma-separated pair consisting of
'LittleTrap' and a logical:
true— Use the Albrecher et al formulation.false— Use the original Heston formation.
Data Types: logical
Number of grid points in the characteristic function variable and in each column
of the log-strike grid, specified as the comma-separated pair consisting of
'NumFFT' and a scalar numeric value.
Data Types: double
Characteristic function variable grid spacing, specified as the comma-separated
pair consisting of 'CharacteristicFcnStep' and a scalar numeric
value.
Data Types: double
Log-strike grid spacing, specified as the comma-separated pair consisting of
'LogStrikeStep' and a scalar numeric value.
Note
If
(LogStrikeStep*CharacteristicFcnStep) is
2*pi/NumFFT, FFT is used. Otherwise,
FRFT is used.
Data Types: double
Damping factor for Carr-Madan formulation, specified as the comma-separated pair
consisting of 'DampingFactor' and a scalar numeric value.
Data Types: double
Type of quadrature, specified as the comma-separated pair consisting of
'Quadrature' and a single character vector or string array with a
value of 'simpson' or 'trapezoidal'.
Data Types: char | string
Flag to expand the outputs, specified as the comma-separated pair consisting of
'ExpandOutput' and a logical:
true— Iftrue, the outputs areNRows-by-NColumnsmatrices.NRowsis the number of strikes for each column and it is determined by theStrikeinput. For example,Strikecan be aNRows-by-1vector, or aNRows-by-NColumnsmatrix. IfStrikeis empty,NRowsis equal toNumFFT.NColumnsis determined by the sizes ofAssetPrice,Settle,Maturity, andOptSpec, which must all be either scalar orNColumns-by-1vectors.false— Iffalse, the outputs areNINST-by-1vectors. Also, the inputsStrike,AssetPrice,Settle,Maturity, andOptSpecmust all be either scalar orNINST-by-1vectors.
Data Types: logical
Output Arguments
Option prices, returned as a NINST-by-1, or
NRows-by-NColumns, depending on
ExpandOutput.
Strikes corresponding to Price, returned as a
NINST-by-1, or
NRows-by-NColumns, depending on
ExpandOutput.
More About
A vanilla option is a category of options that includes only the most standard components.
A vanilla option has an expiration date and straightforward strike price. American-style options and European-style options are both categorized as vanilla options.
The payoff for a vanilla option is as follows:
For a call:
For a put:
where:
St is the price of the underlying asset at time t.
K is the strike price.
For more information, see Vanilla Option.
The Heston model is an extension of the Black-Scholes model, where the volatility (square root of variance) is no longer assumed to be constant, and the variance now follows a stochastic (CIR) process. This process allows modeling the implied volatility smiles observed in the market.
The stochastic differential equation is:
where
r is the continuous risk-free rate.
q is the continuous dividend yield.
St is the asset price at time t.
vt is the asset price variance at time t
v0 is the initial variance of the asset price at t = 0 for (v0 > 0).
θ is the long-term variance level for (θ > 0).
κ is the mean reversion speed for the variance for (κ > 0).
σv is the volatility of the variance for (σv > 0).
p is the correlation between the Wiener processes Wt and Wvt for (-1 ≤ p ≤ 1).
The characteristic function for j = 1 (asset price measure) and j = 2 (risk-neutral measure) is:
where
ϕ is the characteristic function variable.
ƛVolRisk is the volatility risk premium.
τ is the time to maturity (τ = T - t).
i is the unit imaginary number (i2 = -1).
The definitions for Cj and Dj under “The Little Heston Trap” by Albrecher et al. (2007) are:
The Carr and Madan (1999) formulation is a popular modified implementation of Heston (1993) framework.
Rather than computing the probabilities P1 and P2 as intermediate steps, Carr and Madan developed an alternative expression so that taking its inverse Fourier transform gives the option price itself directly.
where
τ is the continuous risk-free rate.
q is the continuous dividend yield.
St is the asset price at time t.
τ is time to maturity (τ = T-t).
Call(K) is the call price at strike K.
Put(K) is the put price at strike K
i is a unit imaginary number (i2= -1)
ϕ is the characteristic function variable.
α is the damping factor.
u is the characteristic function variable for integration, where ϕ = (u - (α+1)i).
f2(ϕ) is the characteristic function for P2.
P2 is the probability of St > K under the risk-neutral measure for the model.
To apply FFT or FRFT to this formulation, the characteristic function variable for
integration, u, is discretized into
NumFFT(N) points with the step size
CharacteristicFcnStep (Δu), and the log-strike
k is discretized into N points with the step size
LogStrikeStep(Δk).
The discretized characteristic function variable for integration, uj(for j = 1,2,3,…,N), has a minimum value of 0 and a maximum value of (N-1) (Δu), and it approximates the continuous integration range from 0 to infinity.
The discretized log-strike grid,
kn(for n =
1, 2, 3, N) is approximately centered around
ln(St),
with a minimum value of
and a maximum value of
Where the minimum allowable strike is
and the maximum allowable strike is
As a result of the discretization, the expression for the call option becomes
where
Δu is the step size of discretized characteristic function variable for integration.
Δk is the step size of discretized log-strike.
N is the number of FFT or FRFT points.
wj is the weights for quadrature used for approximating the integral.
FFT is used to evaluate the above expression if Δk and Δu are subject to the following constraint:
otherwise, the functions use the FRFT method described in Chourdakis (2005).
References
[1] Albrecher, H., Mayer, P., Schoutens, W., and Tistaert, J. "The Little Heston Trap." Working Paper, Linz and Graz University of Technology, K.U. Leuven, ING Financial Markets, 2006.
[2] Carr, P. and D.B. Madan. “Option Valuation using the Fast Fourier Transform.” Journal of Computational Finance. Vol 2. No. 4. 1999.
[3] Chourdakis, K. “Option Pricing Using Fractional FFT.” Journal of Computational Finance. 2005.
[4] Heston, S. L. “A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options.” The Review of Financial Studies. Vol 6. No. 2. 1993.
Version History
Introduced in R2018aAlthough optByHestonFFT supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)