Model Suburban Commuting Using Subtractive Clustering and ANFIS
This example shows how to model the relationship between the number of automobile trips generated from an area and the demographics of the area using subtractive clustering and ANFIS tuning.
Load Traffic Data
This example uses demographic and trip data from 100 traffic analysis zones in New Castle County, Delaware. The data set contains five demographic factors as input variables: population, number of dwelling units, vehicle ownership, median household income, and total employment. The data contains one output variable, number of automobile trips.
Load the training and validation data.
load trafficDataThe data set contains 100 data points, 75 for training and 25 for validation. The training input data (datain) and validation input data (valdatain) each have five columns that represent the input variables. The training output data (dataout) and validation output data (valdataout) each have one column that represents the output variable.
Plot the training data.
h = figure; h.Position(3) = 1.5*h.Position(3); subplot(1,2,1) plot(datain) legend("population", ... "number of dwellings", ... "vehicle ownership",... "median income", ... "total employment", ... Location="northwest") title("Input Variables") xlabel("Data Point") subplot(1,2,2) plot(dataout) legend("number of trips") title("Output Variable") xlabel("Data Point")

Cluster Data
Subtractive clustering is a fast one-pass algorithm for estimating the number of clusters and the cluster centers in a data set. To cluster the training data using subtractive clustering, use the subclust function.
[C,S] = subclust([datain dataout],0.5);
For this example, use a cluster influence range of 0.5. This value indicates the range of influence of a cluster when you consider the data space as a unit hypercube. Specifying a small cluster radius usually generates many small clusters in the data, which produces a FIS with many rules. Specifying a large cluster radius usually produces a few large clusters in the data and results in fewer rules.
Each row of C contains the position of a cluster center identified by the clustering algorithm. In this case, the algorithm found three clusters in the data.
C
C = 3×6
1.8770 0.7630 0.9170 18.7500 1.5650 2.1830
0.3980 0.1510 0.1320 8.1590 0.6250 0.6480
3.1160 1.1930 1.4870 19.7330 0.6030 2.3850
Plot the training data along with the cluster centers for two of the input variables.
figure plot(datain(:,5),dataout(:,1),'.',C(:,5),C(:,6),"r*") legend("Data points","Cluster centers",Location="southeast") xlabel("Total Employment") ylabel("Number of Trips") title("Data and Cluster Centers")

The values in S show the range of influence of the cluster centers for each data dimension. All cluster centers have the same set of S values.
S
S = 1×6
1.1621 0.4117 0.6555 7.6139 2.8931 1.4395
Generate Fuzzy Inference System Using Data Clusters
Use the genfis function to generate a fuzzy inference system (FIS) from the data using subtractive clustering.
An important advantage of using a clustering method to find rules is that the resultant rules are more tailored to the input data than they are in a FIS generated without clustering. This tailoring reduces the total number of rules when the input data has a high dimension.
First, create a genfisOptions option set for subtractive clustering, specifying the same cluster influence range value.
fisOpt = genfisOptions("SubtractiveClustering",... ClusterInfluenceRange=0.5);
Generate the FIS model using the training data and the specified options.
fis = genfis(datain,dataout,fisOpt);
Based on the dimensions of the input and output training data, the generated FIS has five inputs and one output. genfis assigns default names for inputs, outputs, and membership functions.
The generated FIS object is a first-order Sugeno system with three rules.
showrule(fis,Format="symbolic")ans = 3×132 char array
'1. (in1==in1cluster1) & (in2==in2cluster1) & (in3==in3cluster1) & (in4==in4cluster1) & (in5==in5cluster1) => (out1=out1cluster1) (1)'
'2. (in1==in1cluster2) & (in2==in2cluster2) & (in3==in3cluster2) & (in4==in4cluster2) & (in5==in5cluster2) => (out1=out1cluster2) (1)'
'3. (in1==in1cluster3) & (in2==in2cluster3) & (in3==in3cluster3) & (in4==in4cluster3) & (in5==in5cluster3) => (out1=out1cluster3) (1)'
You can conceptualize each rule as follows: If the inputs to the FIS (population, dwelling units, number of vehicles, income, and employment) strongly belong to their representative membership functions for a cluster, then the output (number of trips) must belong to the same cluster. That is, each rule succinctly maps a cluster in the input space to the same cluster in the output space.
Each input and output variable has three membership functions, which correspond to the three identified clusters. The parameters of the input and output membership functions are derived based on the cluster centers and cluster ranges of influence. As an example, plot the membership functions for the first input variable.
figure
plotmf(fis,"input",1)
Evaluate Initial FIS Performance
Apply the training input values to the fuzzy system and find corresponding output values.
fuzout = evalfis(fis,datain);
Compute the root mean squared error (RMSE) of the output values of the fuzzy system compared to the expected output values.
trnRMSE = norm(fuzout-dataout)/sqrt(length(fuzout))
trnRMSE = 0.5276
Validate the performance of the fuzzy system using the validation data.
valfuzout = evalfis(fis,valdatain); valRMSE = norm(valfuzout-valdataout)/sqrt(length(valfuzout))
valRMSE = 0.6179
Plot the output of the model against the validation data.
figure plot(valdataout) hold on plot(valfuzout,"o") hold off ylabel("Output value") legend("Validation data", ... "FIS output", ... Location="northwest")

The plot shows that the model does not predict the validation data well.
Tune FIS Using ANFIS
To improve the FIS performance, you can optimize the system using the anfis function. First, try using a relatively short training period (20 epochs) without using validation data, and then test the resulting FIS model against the validation data.
opt = anfisOptions( ... InitialFIS=fis,... EpochNumber=20,... InitialStepSize=0.1); fis2 = anfis([datain dataout],opt);
ANFIS info: Number of nodes: 44 Number of linear parameters: 18 Number of nonlinear parameters: 30 Total number of parameters: 48 Number of training data pairs: 75 Number of checking data pairs: 0 Number of fuzzy rules: 3 Start training ANFIS ... 1 0.527607 2 0.513727 3 0.492996 4 0.499985 5 0.490585 6 0.492924 Step size decreases to 0.090000 after epoch 7. 7 0.48733 8 0.485036 9 0.480813 Step size increases to 0.099000 after epoch 10. 10 0.475097 11 0.469759 12 0.462516 13 0.451177 Step size increases to 0.108900 after epoch 14. 14 0.447856 15 0.444357 16 0.433904 17 0.433739 Step size increases to 0.119790 after epoch 18. 18 0.420408 19 0.420512 20 0.420275 Designated epoch number reached. ANFIS training completed at epoch 20. Minimal training RMSE = 0.420275
Assess the performance of the FIS on both the training data and the validation data.
fuzout2 = evalfis(fis2,datain); trnRMSE2 = norm(fuzout2-dataout)/sqrt(length(fuzout2))
trnRMSE2 = 0.4203
valfuzout2 = evalfis(fis2,valdatain); valRMSE2 = norm(valfuzout2-valdataout)/sqrt(length(valfuzout2))
valRMSE2 = 0.5894
The model performance shows substantial improvement with respect to the training data but only slightly with respect to the validation data. Plot the improved model output against the validation data.
figure plot(valdataout) hold on plot(valfuzout,"o") plot(valfuzout2,"x") hold off ylabel("Output value") legend("Validation data",... "Initial FIS: RMSE = " + valRMSE, ... "Tuned FIS: RMSE = " + valRMSE2, ... Location="northwest")

Check ANFIS Result for Overfitting
When tuning a FIS, you can detect overfitting when the validation error starts to increase while the training error continues to decrease.
To check the model for overfitting, use anfis with validation data to train the model for 200 epochs. First configure the ANFIS training options by modifying the existing anfisOptions option set. Specify the number of epochs and validation data. Since the number of training epochs is larger, suppress the display of training information in the Command Window.
opt.EpochNumber = 200; opt.ValidationData = [valdatain valdataout]; opt.DisplayANFISInformation = 0; opt.DisplayErrorValues = 0; opt.DisplayStepSize = 0; opt.DisplayFinalResults = 0;
Train the FIS.
[fis3,trnErr,stepSize,fis4,valErr] = anfis([datain dataout],opt);
Here:
fis3is the FIS object when the training error reaches a minimum.fis4is the snapshot FIS object when the validation data error reaches a minimum.stepSizeis a history of the training step sizes.trnErris the RMSE using the training data.valErris the RMSE using the validation data for each training epoch.
After the training completes, validate the model using the training and validation data.
fuzout4 = evalfis(fis4,datain); trnRMSE4 = norm(fuzout4-dataout)/sqrt(length(fuzout4))
trnRMSE4 = 0.3393
valfuzout4 = evalfis(fis4,valdatain); valRMSE4 = norm(valfuzout4-valdataout)/sqrt(length(valfuzout4))
valRMSE4 = 0.5834
The error with the training data is the lowest thus far, and the error with the validation data is also slightly lower than before. This result suggests possible overfitting, which occurs when you fit the fuzzy system to the training data so well that it no longer does a good job of fitting the validation data. The result is a loss of generality.
View the improved model output. Plot the model output against the validation data.
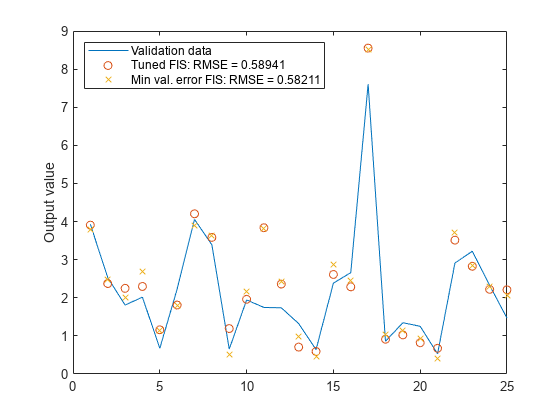
figure plot(valdataout) hold on plot(valfuzout2,"o") plot(valfuzout4,"x") hold off ylabel("Output value") legend("Validation data",... "Tuned FIS: RMSE = " + valRMSE2, ... "Min val. error FIS: RMSE = " + valRMSE4, ... Location="northwest")
Next, plot the training error trnErr.
figure plot(trnErr) title("Training Error") xlabel("Number of Epochs") ylabel("Error")

This plot shows that the training error settles at about the 60th epoch.
Plot the validation error valErr.
figure plot(valErr) title("Validation Error") xlabel("Number of Epochs") ylabel("Error")

The plot shows that the smallest value of the validation data error occurs at epoch 52. After this point, it increases slightly even as anfis continues to minimize the error against the training data. This pattern is a sign of overfitting. Depending on the specified error tolerance, plotting the validation error can also indicate the ability of the model to generalize the test data.