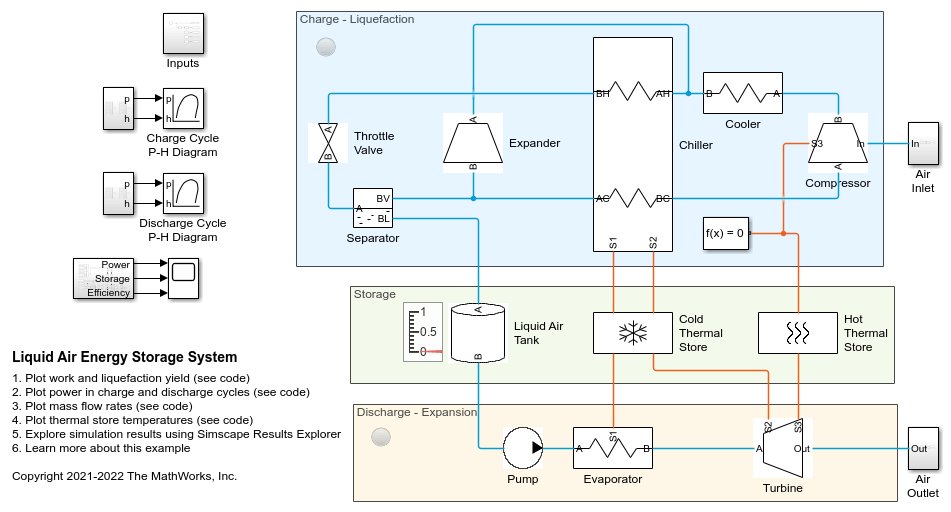
Positive-Displacement Compressor (2P)

Two-phase fluid positive-displacement compressor in a thermodynamic cycle

Since R2022a

• 

Libraries:
Simscape / Fluids / Two-Phase Fluid / Fluid Machines

Description

The Positive-Displacement Compressor (2P) block represents a positive-displacement compressor, such as reciprocating piston, rotary screw, rotary vane, and scroll, in a two-phase fluid network. You can control how the block parameterizes a positive displacement compressor by setting Parameterization to Analytical or Tabulated. Port R and port C are mechanical rotational conserving ports associated with the compressor shaft and casing, respectively. When there is positive rotation at port R with respect to port C, two-phase fluid flows from port A to port B. The block may not be accurate for reversed flow.

The block treats the positive displacement process as polytropic such that pvⁿ is constant, where p is pressure, v is specific volume, and n is the Polytropic exponent parameter. You can use the block to model isentropic processes by setting n equal to the isentropic exponent, k. The figure shows the steps of a positive-displacement compressor on a P-V diagram, which has these states:

• a — The compressor cylinder is full at inlet pressure.

• b — The pressure inside the compressor exceeds that of the outlet, which results in fluid discharge.

• c — The compressor reaches the top of the piston stroke, and only the clearance volume remains in the cylinder.

• d — The pressure inside the cylinder drops below the inlet pressure, which results in fluid intake.

Efficiency

When you set Volumetric efficiency parameterization to Analytical, the block calculates the volumetric efficiency as

$${\eta }_V=1+C-C{\left(\frac{p_{out}}{p_{in}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.},$$

where the block implements the polytropic pressure-volume relationship. The block calculates the clearance volume fraction, C, as

$$C=\frac{1-{\eta }_{V_{nominal}}}{p_{ratio}{}^{1/n}-1},$$

where η_Vnominal is the Nominal volumetric efficiency parameter, and p_ratio is the ratio of saturation pressures that correspond to Nominal condensing temperature and Nominal evaporating temperature.

When you set Volumetric efficiency parameterization to

Tabulated, the block interpolates the values of the Volumetric efficiency table, eta(pr,w) parameter as a function of the shaft speed and the pressure ratio.

Continuity Equations

The block calculates the mass flow rate as

$$\dot{m}={\eta }_V\omega \frac{V_{disp}}{v_s},$$

where

• ṁ is the mass flow rate.

• ω is the angular velocity of port R relative to port C.

• v_s is the specific volume at the inlet.

• V_disp is the displacement volume that the block uses.

When you set Displacement specification to Volumetric displacement, the block uses the Displacement volume parameter. When you set Displacement specification to Nominal mass flow rate and shaft speed, the block calculates the displacement volume as

$$V_{disp}=\frac{{\dot{m}}_{nominal}{v}_{s,nominal}}{{\omega }_{nominal}{\eta }_{V_{nominal}}},$$

where

• ṁ_nominal is the Nominal mass flow rate parameter.

• ω_nominal is the Nominal shaft speed parameter.

• η_Vnominal is the Nominal volumetric efficiency parameter.

The block calculates the nominal inlet specific volume, v_s, based upon the Nominal conditions specification parameter. When you select Nominal pressure ratio, the block uses the Nominal inlet pressure and Nominal inlet temperature parameters. When you select Nominal evaporating and condensing temperatures, the block uses the Nominal evaporating temperature and Nominal evaporator superheat parameters.

The block conserves mass such that

$${\dot{m}}_A+{\dot{m}}_B=0,$$

where ṁ_A and ṁ_B are the mass flow rates of ports A and B, respectively. The block conserves energy such that

$${\varphi }_A+{\varphi }_B+{\dot{m}}_A\Delta h_t=0,$$

where Δh_t is the change in specific total enthalpy, and ṁ_AΔh_t is the fluid power.

The block equates the fluid power to the polytropic power such that

$${\eta }_M\tau =\frac{n}{n-1}{\eta }_V{p}_{in}{V}_{disp}\left[{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{n-1}{n}}-1\right],$$

where η_M is the Mechanical efficiency parameter, and τ is the shaft torque.

Visualizing the Volumetric Efficiency

To visualize the block volumetric efficiency, right-click the block and select Fluids > Plot Volumetric Efficiency.

Each time you modify the block settings, click Reload Data on the figure window.

When you set Volumetric efficiency parameterization to Analytical, the block plots compressor volumetric efficiency vs. pressure ratio.

Analytical Parameterization Default Volumetric Efficiency

When you set Volumetric efficiency parameterization to Tabulated, the block plots compressor volumetric efficiency vs. pressure ratio for each entry in the Shaft speed vector, w.

Tabulated Parameterization Default Volumetric Efficiency

Assumptions and Limitations

• The block may not be accurate for flow from port B to port A.

• The block assumes that the flow is quasi-steady: the compressor does not accumulate mass.

• The block is designed to operate in superheated vapor. The block may not be accurate in two-phase mixture or subcooled liquid.

Ports

Conserving

A — Compressor inlet

two-phase fluid

Two-phase fluid conserving port associated with the compressor inlet.

B — Compressor outlet

two-phase fluid

Two-phase fluid conserving port associated with the compressor outlet.

C — Compressor casing

mechanical rotational

Mechanical rotational conserving port associated with the compressor case.

R — Compressor shaft

mechanical rotational

Mechanical rotational conserving port associated with the compressor shaft.

Parameters

Displacement specification — Option to specify displacement by volume or nominal conditions

Volumetric displacement (default) | Nominal mass flow rate and shaft speed

Whether to specify the fluid displacement according to volume per cycle or nominal condition values.

Displacement volume — Displacement volume

130 cm^3/rev (default) | positive scalar

Fluid volume displaced per cycle. The block defines a cycle as one compression stroke and one expansion stroke, which occur during a single crank shaft revolution. This volume is the difference between the maximum cylinder volume and the clearance volume, (V_a-V_c). In general, the displacement volume is the volume swept out by the compressor over one shaft revolution.

Dependencies

To enable this parameter, set Displacement specification to Volumetric displacement.

Nominal conditions specification — Option to specify pressure ratio or refrigeration cycle saturation temperatures

Nominal pressure ratio (default) | Nominal evaporating and condensing temperatures

Whether to specify the nominal conditions that determine the displacement volume using the nominal outlet to inlet pressure ratio or the nominal evaporating and condensing temperatures.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed.

Nominal mass flow rate — Nominal mass flow rate

0.01 kg/s (default) | positive scalar

Nominal mass flow rate that the block uses to find the displacement volume.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed.

Nominal shaft speed — Nominal shaft speed

1000 rpm (default) | positive scalar

Nominal shaft speed that the block uses to find the displacement volume.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed.

Nominal inlet pressure — Nominal inlet pressure

0.101325 MPa (default) | positive scalar

Nominal inlet pressure that the block uses the find the displacement volume.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed and Nominal conditions specification to Nominal pressure ratio.

Nominal inlet temperature — Nominal inlet temperature

373.15 K (default) | positive scalar

Nominal inlet temperature that the block uses to find the displacement volume.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed and Nominal conditions specification to Nominal pressure ratio.

Nominal evaporating temperature — Nominal evaporating temperature

373.15 K (default) | positive scalar

Nominal evaporating temperature that the block uses the find the displacement volume. This is the saturation temperature in the evaporator. The block assumes the nominal compressor inlet pressure is the pressure that corresponds to this saturation temperature.

The evaporating temperature is also known as the saturated suction temperature, or SST.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed and Nominal conditions specification to Nominal evaporating and condensing temperatures.

Nominal condensing temperature — Nominal condensing temperature

398.15 K (default)

Nominal condensing temperature that the block uses to find the displacement volume. This is the saturation temperature in the condenser. The block assumes that the nominal compressor outlet pressure is the pressure that corresponds to this saturation temperature.

The condensing temperature is also known as the saturated discharge temperature, or SDT.

Dependencies

To enable this parameter, set Displacement specification to Nominal mass flow rate and shaft speed and Nominal conditions specification to Nominal evaporating and condensing temperatures.

Nominal evaporator superheat — Nominal saturation excess temperature

10 deltaK (default) | scalar

Nominal excess temperature beyond the saturation point in the evaporator outlet, which the block assumes to be connected to the compressor inlet.

Dependencies

To enable this parameter, set Nominal conditions specification to Nominal evaporating and condensing temperatures.

Volumetric efficiency parameterization — Option to parameterize volumetric efficiency analytically or using tables

Analytical (default) | Tabulated

Whether to parameterize the displacement volumetric efficiency using analytical equations or tabulated data.

Nominal volumetric efficiency — Nominal volumetric efficiency

0.95 (default) | positive scalar

Nominal volumetric efficiency to compute the clearance volume fraction. The nominal volumetric efficiency is the volumetric efficiency when the compressor operates at nominal conditions.

Dependencies

To enable this parameter, set Volumetric efficiency parameterization to Analytical.

Nominal pressure ratio — Nominal pressure ratio

5 (default)

Nominal pressure ratio to compute the clearance volume fraction.

Dependencies

To enable this parameter, set Nominal conditions specification to Nominal pressure ratio and Volumetric efficiency parameterization to Analytical.

Shaft speed vector, w — Shaft speed vector

[800, 1500, 2800, 3300, 4000] rpm (default) | vector of length M

Vector of shaft speeds corresponding to the compressor volumetric efficiency. Each element corresponds to a row of the Volumetric efficiency table, eta(pr,w) parameter.

Dependencies

To enable this parameter, set Nominal conditions specification to Nominal pressure ratio and Volumetric efficiency parameterization to Tabulated.

Pressure ratio vector, pr — Pressure ratio vector

[2, 4, 6, 8] (default) | vector of length N

Vector of pressure ratios corresponding to the compressor volumetric efficiency. Each element corresponds to a column of the Volumetric efficiency table, eta(pr,w) parameter.

Dependencies

To enable this parameter, set Nominal conditions specification to Nominal pressure ratio and Volumetric efficiency parameterization to Tabulated.

Volumetric efficiency table, eta(pr,w) — Volumetric efficiency

[.95, .9, .85, .8, .75; .925, .875, .825, .775, .725; .875, .825, .775, .725, .675; .75, .7, .65, .6, .55] (default) | M-by-N matrix

Volumetric efficiency for a given shaft speed and pressure ratio.

Dependencies

To enable this parameter, set Nominal conditions specification to Nominal pressure ratio and Volumetric efficiency parameterization to Tabulated.

Polytropic exponent — Polytropic exponent

1.2 (default) | positive scalar

Exponent that the block uses when implementing the polytropic pressure-volume relationship.

Mechanical efficiency — Compressor mechanical efficiency

0.9 (default) | positive scalar

Ratio of the fluid power to the mechanical shaft power.

Inlet area at port A — Inlet area

0.01 m^2 (default) | positive scalar

Inlet area associated with port A.

Outlet area at port B — Outlet area

0.01 m^2 (default) | positive scalar

Outlet area associated with port B.

Report when fluid is not fully vapor — Two-phase fluid condition check

None (default) | Warning | Error

Action to perform when the fluid at port A does not meet vapor conditions.

References

[1] Mitchell and Braun, Principles of Heating, Ventilation, and Air Conditioning in Buildings, chap. SM6, 2012.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2022a