ifanbeam
Inverse fan-beam transform
Description
I = ifanbeam(F,D)I from fan-beam
projection data in F. Each column of
F contains fan-beam projection data at
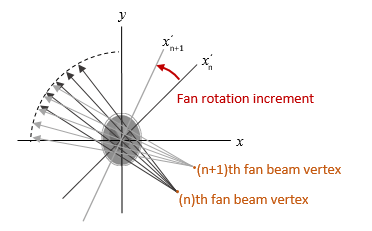
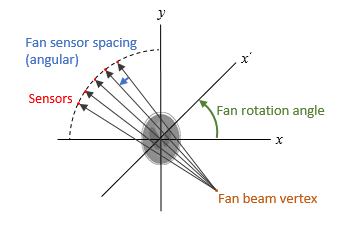
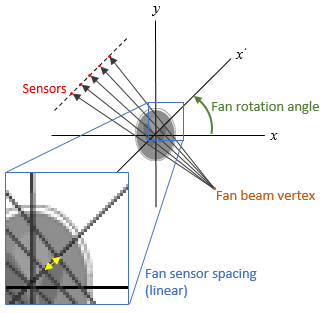
one rotation angle. The angle between sensors is assumed to be
uniform and equal to the increment between fan-beam rotation angles.
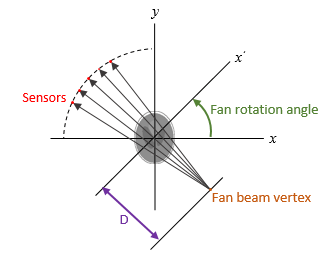
D is the distance from the fan-beam
vertex to the center of rotation.
I = ifanbeam(F,D,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
Algorithms
ifanbeam converts the fan-beam data to parallel beam
projections and then uses the filtered back projection algorithm to perform
the inverse Radon transform. The filter is designed directly in the
frequency domain and then multiplied by the FFT of the projections. The
projections are zero-padded to a power of 2 before filtering to prevent
spatial domain aliasing and to speed up the FFT.
References
[1]
Version History
Introduced before R2006a