imimposemin

Impose minima

Syntax

J = imimposemin(I,BW)

J = imimposemin(I,BW,conn)

Description

J = imimposemin(I,BW) modifies the grayscale mask image I using morphological reconstruction so it only has regional minima wherever binary marker image BW is nonzero.

J = imimposemin(I,BW,conn) specifies the pixel connectivity for the morphological reconstruction.

Examples

Impose Regional Minimum at One Location

This example shows how to modify an image so that one area is always a regional minimum.

Read an image and display it. This image is called the mask image.

mask = imread('glass.png');
imshow(mask)

Create a binary image that is the same size as the mask image and sets a small area of the binary image to 1. These pixels define the location in the mask image where a regional minimum will be imposed. The resulting image is called the marker image.

marker = false(size(mask));
marker(65:70,65:70) = true;

Superimpose the marker over the mask to show where these pixels of interest fall on the original image. The small white square marks the spot. This code is not essential to the impose minima operation.

J = mask;
J(marker) = 255;
figure
imshow(J)
title('Marker Image Superimposed on Mask')

Impose the regional minimum on the input image using the imimposemin function. Note how all the dark areas of the original image, except the marked area, are lighter.

K = imimposemin(mask,marker);
figure
imshow(K)

To illustrate how this operation removes all minima in the original image except the imposed minimum, compare the regional minima in the original image with the regional minimum in the processed image. These calls to imregionalmin return binary images that specify the locations of all the regional minima in both images.

BW = imregionalmin(mask);
figure
subplot(1,2,1)
imshow(BW)  
title('Regional Minima in Original Image')

BW2 = imregionalmin(K);
subplot(1,2,2)
imshow(BW2)
title('Regional Minima After Processing')

Input Arguments

I — Grayscale mask image

numeric array

Grayscale mask image, specified as a numeric array of any dimension.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

BW — Binary marker image

numeric array | logical array

Binary marker image, specified as a numeric or logical array of the same size as the grayscale mask image I. For numeric input, any nonzero pixels are considered to be 1 (true).

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical

conn — Pixel connectivity

4 | 8 | 6 | 18 | 26 | 3-by-3-by- ... -by-3 matrix of 0s and 1s

Pixel connectivity, specified as one of the values in this table. The default connectivity is 8 for 2-D images, and 26 for 3-D images.

Value	Meaning
Two-Dimensional Connectivities
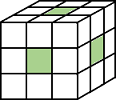
4-connected	Pixels are connected if their edges touch. The neighborhood of a pixel are the adjacent pixels in the horizontal or vertical direction.
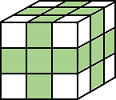
8-connected	Pixels are connected if their edges or corners touch. The neighborhood of a pixel are the adjacent pixels in the horizontal, vertical, or diagonal direction.
Three-Dimensional Connectivities
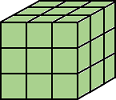
6-connected	Pixels are connected if their faces touch. The neighborhood of a pixel are the adjacent pixels in: One of these directions: in, out, left, right, up, and down
18-connected	Pixels are connected if their faces or edges touch. The neighborhood of a pixel are the adjacent pixels in: One of these directions: in, out, left, right, up, and down A combination of two directions, such as right-down or in-up
26-connected	Pixels are connected if their faces, edges, or corners touch. The neighborhood of a pixel are the adjacent pixels in: One of these directions: in, out, left, right, up, and down A combination of two directions, such as right-down or in-up A combination of three directions, such as in-right-up or in-left-down

For higher dimensions, imimposemin uses the default value conndef(ndims(I),'maximal').

Connectivity can also be defined in a more general way for any dimension by specifying a 3-by-3-by- ... -by-3 matrix of 0s and 1s. The 1-valued elements define neighborhood locations relative to the center element of conn. Note that conn must be symmetric about its center element. See Specifying Custom Connectivities for more information.

Data Types: double | logical

Output Arguments

J — Reconstructed image

numeric array

Reconstructed image, returned as a numeric or logical array of the same size and data type as I.

Algorithms

imimposemin uses a technique based on morphological reconstruction.