regionprops

Measure properties of image regions

Syntax

stats = regionprops(BW,properties)

stats = regionprops(CC,properties)

stats = regionprops(L,properties)

stats = regionprops(___,I,properties)

stats = regionprops(output,___)

Description

stats = regionprops(BW,properties) returns measurements for the set of properties specified by properties for each 8-connected component (object) in the binary image, BW. stats is struct array containing a struct for each object in the image. You can use regionprops on contiguous regions and discontiguous regions (see Algorithms).

Note

To return measurements of a 3-D volumetric image, consider using regionprops3. While regionprops can accept 3-D images, regionprops3 calculates more statistics for 3-D images than regionprops.

For all syntaxes, if you do not specify the properties argument, then regionprops returns the 'Area', 'Centroid', and 'BoundingBox' measurements.

You optionally can measure properties of image regions using a GPU (requires Parallel Computing Toolbox™). The 'ConvexArea', 'ConvexHull', 'ConvexImage', 'Circularity', 'EulerNumber', 'FilledArea', 'FilledImage', 'MaxFeretProperties', 'MinFeretProperties' and 'Solidity' properties are not supported on a GPU.

stats = regionprops(CC,properties) measures a set of properties for each connected component (object) in CC, which is a structure returned by bwconncomp.

This syntax is not supported on a GPU.

stats = regionprops(L,properties) measures a set of properties for each labeled region in label matrix L.

stats = regionprops(___,I,properties) returns measurements for the set of properties specified by properties for each labeled region in the image I. The first input to regionprops (BW, CC, or L) identifies the regions in I.

stats = regionprops(output,___) returns measurements for a set of properties, where output specifies the type of return value. regionprops can return measurements in a struct array or a table.

The 'table' output value is not supported on a GPU.

Examples

Calculate Centroids and Superimpose Locations on Image

Read a binary image into workspace.

BW = imread('text.png');

Calculate centroids for connected components in the image using regionprops. The regionprops function returns the centroids in a structure array.

s = regionprops(BW,'centroid');

Store the x- and y-coordinates of the centroids into a two-column matrix.

centroids = cat(1,s.Centroid);

Display the binary image with the centroid locations superimposed.

imshow(BW)
hold on
plot(centroids(:,1),centroids(:,2),'b*')
hold off

Estimate Center and Radii of Circular Objects and Plot Circles

Estimate the center and radii of circular objects in an image and use this information to plot circles on the image. In this example, regionprops returns the measured region properties in a table.

Read an image into workspace.

a = imread('circlesBrightDark.png');

Turn the input image into a binary image.

bw = a < 100;
imshow(bw)
title('Image with Circles')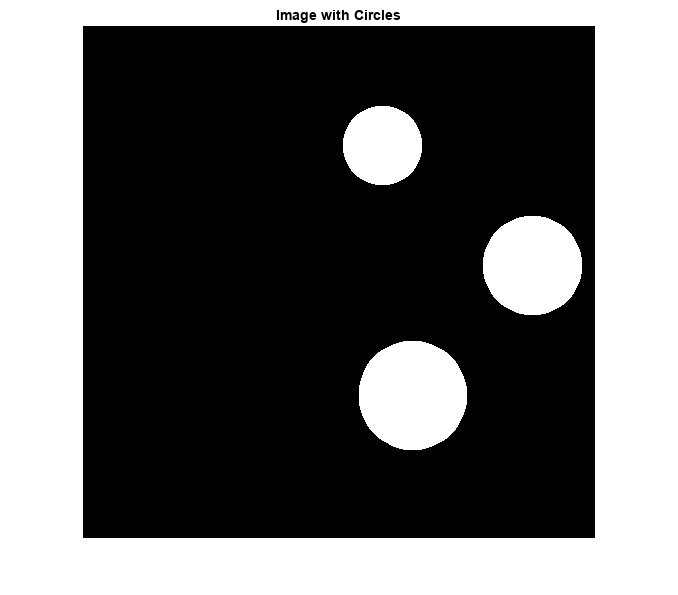

Calculate properties of regions in the image and return the data in a table.

stats = regionprops('table',bw,'Centroid',...
    'MajorAxisLength','MinorAxisLength')

stats=4×3 table
        Centroid        MajorAxisLength    MinorAxisLength
    ________________    _______________    _______________

     256.5     256.5        834.46             834.46     
       300       120        81.759             81.759     
    330.47    369.83        111.78             110.36     
       450       240        101.72             101.72     

Get centers and radii of the circles.

centers = stats.Centroid;
diameters = mean([stats.MajorAxisLength stats.MinorAxisLength],2);
radii = diameters/2;

Plot the circles.

hold on
viscircles(centers,radii);
hold off

Input Arguments

BW — Binary image

logical array of any dimension

Binary image, specified as a logical array of any dimension.

Data Types: logical

CC — Connected components

structure

Connected components, specified as a structure returned by bwconncomp.

Data Types: struct

L — Label matrix

numeric array

Label matrix, specified as a numeric array of any dimension. regionprops treats negative-valued pixels as background and rounds down input pixels that are not integers. Positive integer elements of L correspond to different regions. For example, the set of elements of L equal to 1 corresponds to region 1; the set of elements of L equal to 2 corresponds to region 2; and so on.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32

properties — Type of measurement

comma-separated list of string scalars or character vectors | cell array of string scalars or character vectors | 'all' | 'basic'

Type of measurement, specified as a comma-separated list of string scalars or character vectors, a cell array of string scalars or character vectors, or as 'all' or 'basic'. Property names are case-insensitive and can be abbreviated. When used with code generation, regionprops does not support cell arrays of string scalars or character vectors.

• If you specify 'all', regionprops computes all the shape measurements and, for grayscale images, the pixel value measurements as well.

• If you specify 'basic', or do not specify the properties argument, regionprops computes only the 'Area', 'Centroid', and 'BoundingBox' measurements.

The following tables list all the properties that provide shape measurements. The properties listed in the Pixel Value Measurements table are valid only when you specify a grayscale image.

Shape Measurements

Property Name	Description	N-D Support	GPU Support	Code Generation
'Area'	Actual number of pixels in the region, returned as a scalar. (This value might differ slightly from the value returned by bwarea, which weights different patterns of pixels differently.) To find the equivalent to the area of a 3-D volume, use the 'Volume' property of regionprops3.	Yes	Yes	Yes
'BoundingBox'	Smallest rectangle containing the region, returned as a 1-by-Q*2 vector, where Q is the number of image dimensions. For example, in the vector [ul_corner width], ul_corner specifies the upper-left corner of the bounding box in the form [x y z ...]. width specifies the width of the bounding box along each dimension in the form [x_width y_width ...]. regionprops uses ndims to get the dimensions of label matrix or binary image, ndims(L), and numel to get the dimensions of connected components, numel(CC.ImageSize).	Yes	Yes	Yes
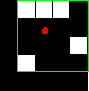
'Centroid'	Center of mass of the region, returned as a 1-by-Q vector. The first element of Centroid is the horizontal coordinate (or x-coordinate) of the center of mass. The second element is the vertical coordinate (or y-coordinate). All other elements of Centroid are in order of dimension. This figure illustrates the centroid and bounding box for a discontiguous region. The region consists of the white pixels; the green box is the bounding box, and the red dot is the centroid.	Yes	Yes	Yes
'ConvexArea'	Number of pixels in 'ConvexImage', returned as a scalar.	2-D only	No	No
'ConvexHull'	Smallest convex polygon that can contain the region, returned as a p-by-2 matrix. Each row of the matrix contains the x- and y-coordinates of one vertex of the polygon.	2-D only	No	No
'ConvexImage'	Image that specifies the convex hull, with all pixels within the hull filled in (set to on), returned as a binary image (logical). The image is the size of the bounding box of the region. (For pixels that the boundary of the hull passes through, regionprops uses the same logic as roipoly to determine whether the pixel is inside or outside the hull.)	2-D only	No	No
'Circularity'	Circularity that specifies the roundness of objects, returned as a struct with field Circularity. The struct contains the circularity value for each object in the input image. The circularity value is computed as (4*Area*pi)/(Perimeter2). For a perfect circle, the circularity value is 1. The input must be a label matrix or binary image with contiguous regions. If the image contains discontiguous regions, regionprops returns unexpected results. Circularity is not recommended for very small objects such as a 3*3 square. For such cases the results might exceed the circularity value for a perfect circle which is 1.	2-D only	No	Yes
'Eccentricity'	Eccentricity of the ellipse that has the same second-moments as the region, returned as a scalar. The eccentricity is the ratio of the distance between the foci of the ellipse and its major axis length. The value is between 0 and 1. (0 and 1 are degenerate cases. An ellipse whose eccentricity is 0 is actually a circle, while an ellipse whose eccentricity is 1 is a line segment.)	2-D only	Yes	Yes
'EquivDiameter'	Diameter of a circle with the same area as the region, returned as a scalar. Computed as sqrt(4*Area/pi).	2-D only	Yes	Yes
'EulerNumber'	Number of objects in the region minus the number of holes in those objects, returned as a scalar. This property is supported only for 2-D label matrices. regionprops uses 8-connectivity to compute the Euler number measurement. To learn more about connectivity, see Pixel Connectivity.	2-D only	No	Yes
'Extent'	Ratio of pixels in the region to pixels in the total bounding box, returned as a scalar. Computed as the Area divided by the area of the bounding box.	2-D only	Yes	Yes
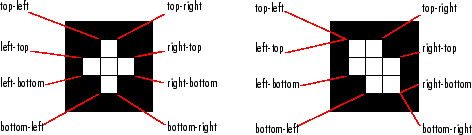
'Extrema'	Extrema points in the region, returned as an 8-by-2 matrix. Each row of the matrix contains the x- and y-coordinates of one of the points. The format of the vector is [top-left top-right right-top right-bottom bottom-right bottom-left left-bottom left-top]. This figure illustrates the extrema of two different regions. In the region on the left, each extrema point is distinct. In the region on the right, certain extrema points (e.g., top-left and left-top) are identical.	2-D only	Yes	Yes
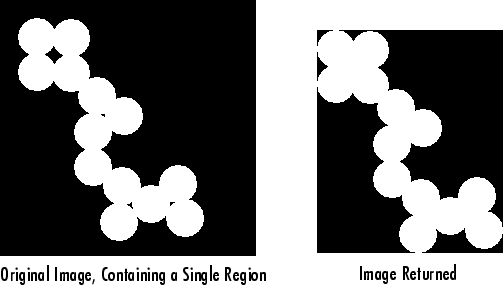
'FilledArea'	Number of on pixels in FilledImage, returned as a scalar.	Yes	No	Yes
'FilledImage'	Image the same size as the bounding box of the region, returned as a binary (logical) array. The on pixels correspond to the region, with all holes filled in, as shown in this figure.	Yes	No	Yes
'Image'	Image the same size as the bounding box of the region, returned as a binary (logical) array. The on pixels correspond to the region, and all other pixels are off.	Yes	Yes	Yes
'MaxFeretProperties'	Feret properties that include maximum Feret diameter, its relative angle, and coordinate values, returned as a struct with fields: Field Description MaxFeretDiameter Maximum Feret diameter measured as the maximum distance between any two boundary points on the antipodal vertices of convex hull that enclose the object. MaxFeretAngle Angle of the maximum Feret diameter with respect to horizontal axis of the image. MaxFeretCoordinates Endpoint coordinates of the maximum Feret diameter. The input can be a binary image, connected component, or a label matrix.	2-D only	No	No
'MinFeretProperties'	Feret properties that include minimum Feret diameter, its relative angle, and coordinate values, returned as a struct with fields: Field Description MinFeretDiameter Minimum Feret diameter measured as the minimum distance between any two boundary points on the antipodal vertices of convex hull that enclose the object. MinFeretAngle Angle of the minimum Feret diameter with respect to horizontal axis of the image. MinFeretCoordinates Endpoint coordinates of the minimum Feret diameter. The input can be a binary image, a connected component, or a label matrix.	2-D only	No	No
'MajorAxisLength'	Length (in pixels) of the major axis of the ellipse that has the same normalized second central moments as the region, returned as a scalar.	2-D only	Yes	Yes
'MinorAxisLength'	Length (in pixels) of the minor axis of the ellipse that has the same normalized second central moments as the region, returned as a scalar.	2-D only	Yes	Yes
'Orientation'	Angle between the x-axis and the major axis of the ellipse that has the same second-moments as the region, returned as a scalar. The value is in degrees, ranging from -90 degrees to 90 degrees. This figure illustrates the axes and orientation of the ellipse. The left side of the figure shows an image region and its corresponding ellipse. The right side shows the same ellipse with the solid blue lines representing the axes. The red dots are the foci. The orientation is the angle between the horizontal dotted line and the major axis.	2-D only	Yes	Yes
'Perimeter'	Distance around the boundary of the region returned as a scalar. regionprops computes the perimeter by calculating the distance between each adjoining pair of pixels around the border of the region. If the image contains discontiguous regions, regionprops returns unexpected results. This figure illustrates the pixels included in the perimeter calculation for this object.	2-D only	Yes	Yes
'PixelIdxList'	Linear indices of the pixels in the region, returned as a p-element vector.	Yes	Yes	Yes
'PixelList'	Locations of pixels in the region, returned as a p-by-Q matrix. Each row of the matrix has the form [x y z ...] and specifies the coordinates of one pixel in the region.	Yes	Yes	Yes
'Solidity'	Proportion of the pixels in the convex hull that are also in the region, returned as a scalar. Computed as Area/ConvexArea.	2-D only	No	No
'SubarrayIdx'	Elements of L inside the object bounding box, returned as a cell array that contains indices such that L(idx{:}) extracts the elements.	Yes	Yes	No

The pixel value measurement properties in the following table are valid only when you specify a grayscale image, I.

Pixel Value Measurements

Property Name	Description	N-D Support	GPU Support	Code Generation
'MaxIntensity'	Value of the pixel with the greatest intensity in the region, returned as a scalar.	Yes	Yes	Yes
'MeanIntensity'	Mean of all the intensity values in the region, returned as a scalar.	Yes	Yes	Yes
'MinIntensity'	Value of the pixel with the lowest intensity in the region, returned as a scalar.	Yes	Yes	Yes
'PixelValues'	Number of pixels in the region, returned as a p-by-1 vector, where p is the number of pixels in the region. Each element in the vector contains the value of a pixel in the region.	Yes	Yes	Yes
'WeightedCentroid'	Center of the region based on location and intensity value, returned as a p-by-Q vector of coordinates. The first element of WeightedCentroid is the horizontal coordinate (or x-coordinate) of the weighted centroid. The second element is the vertical coordinate (or y-coordinate). All other elements of WeightedCentroid are in order of dimension.	Yes	Yes	Yes

Data Types: char | string | cell

I — Image to be measured

grayscale image

Image to be measured, specified as a grayscale image. The size of the image must match the size of the binary image BW, connected component structure CC, or label matrix L.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32

output — Return type

'struct' (default) | 'table'

Return type, specified as either of the following values.

Value	Description
'struct'	Returns an array of structures with length equal to the number of objects in BW, CC.NumObjects, or max(L(:)). The fields of the structure array denote different properties for each region, as specified by properties.
'table'	Returns a MATLAB® table with height (number of rows) equal to the number of objects in BW, CC.NumObjects, or max(L(:)). The variables (columns) denote different properties for each region, as specified by properties. To learn more about MATLAB tables, see table.

Data Types: char | string

Output Arguments

stats — Measurement values

struct array (default) | table

Measurement values, returned as an array of structs or a table. The number of structs in the array, or the number of rows in the table, corresponds to the number of objects in BW, CC.NumObjects, or max(L(:)). The fields of each struct, or the variables in each row, denote the properties calculated for each region, as specified by properties.

Tips

• The function ismember is useful with regionprops, bwconncomp, and labelmatrix for creating a binary image containing only objects or regions that meet certain criteria. For example, these commands create a binary image containing only the regions whose area is greater than 80 and whose eccentricity is less than 0.8.

  cc = bwconncomp(BW); 
  stats = regionprops(cc, 'Area','Eccentricity'); 
  idx = find([stats.Area] > 80 & [stats.Eccentricity] < 0.8); 
  BW2 = ismember(labelmatrix(cc), idx);  
  

• The comma-separated list syntax for structure arrays is useful when you work with the output of regionprops. For a field that contains a scalar, you can use this syntax to create a vector containing the value of this field for each region in the image. For instance, if stats is a structure array with field Area, then the following expression:

  stats(1).Area, stats(2).Area, ..., stats(end).Area
  

  is equivalent to:

  stats.Area
  

  Therefore, you can use these calls to create a vector containing the area of each region in the image. allArea is a vector of the same length as the structure array stats.

  stats = regionprops(L, 'Area');
  allArea = [stats.Area];
  

• The functions bwlabel, bwlabeln, and bwconncomp all compute connected components for binary images. bwconncomp replaces the use of bwlabel and bwlabeln. It uses less memory and is sometimes faster than the other functions.

  Function	Input Dimension	Output Form	Memory Use	Connectivity
  bwlabel	2-D	Label matrix with double-precision	High	4 or 8
  bwlabeln	N-D	Double-precision label matrix	High	Any
  bwconncomp	N-D	CC struct	Low	Any

  The output of bwlabel and bwlabeln is a double-precision label matrix. To compute a label matrix using a more memory-efficient data type, use the labelmatrix function on the output of bwconncomp:

  CC = bwconncomp(BW);
  L = labelmatrix(CC);

  If you are measuring components in a binary image with default connectivity, it is no longer necessary to call bwlabel or bwlabeln first. You can pass the binary image directly to regionprops, which then uses the memory-efficient bwconncomp function to compute the connected components automatically. To specify nondefault connectivity, call bwconncomp and pass the result to regionprops.

  CC = bwconncomp(BW, CONN);
  S = regionprops(CC);

• Most of the measurements take little time to compute. However, the following measurements can take longer, depending on the number of regions in L:

  • 'ConvexHull'

  • 'ConvexImage'

  • 'ConvexArea'

  • 'FilledImage'

• Computing certain groups of measurements takes about the same amount of time as computing just one of them. regionprops takes advantage of intermediate computations useful to each computation. Therefore, it is fastest to compute all the desired measurements in a single call to regionprops.

Algorithms

Contiguous regions are also called objects, connected components, or blobs. A label matrix containing contiguous regions might look like this:

1 1 0 2 2 0 3 3
1 1 0 2 2 0 3 3

Elements of L equal to 1 belong to the first contiguous region or connected component; elements of L equal to 2 belong to the second connected component; and so on.

Discontiguous regions are regions that might contain multiple connected components. A label matrix containing discontiguous regions might look like this:

1 1 0 1 1 0 2 2
1 1 0 1 1 0 2 2

Elements of L equal to 1 belong to the first region, which is discontiguous and contains two connected components. Elements of L equal to 2 belong to the second region, which is a single connected component.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• regionprops supports the generation of C code (requires MATLAB Coder™). Note that if you choose the generic MATLAB Host Computer target platform, regionprops generates code that uses a precompiled, platform-specific shared library. Use of a shared library preserves performance optimizations but limits the target platforms for which code can be generated. For more information, see Code Generation Using a Shared Library.

• Supports only 2-D input images or label matrices.

• Specifying the output type 'table' is not supported.

• Passing a cell array of properties is not supported. Use a comma-separated list instead.

• All properties are supported except 'ConvexArea', 'ConvexHull', 'ConvexImage', 'MaxFeretProperties', 'MinFeretProperties', 'Solidity', and 'SubarrayIdx'.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

• gpuArray input must be a 2-D logical matrix or a 2-D label matrix.

• The connected component structure (CC) input is not supported.

• The following properties are not supported: 'ConvexArea', 'ConvexHull', 'ConvexImage', 'Circularity','EulerNumber', 'FilledArea', 'FilledImage', 'MaxFeretProperties', 'MinFeretProperties' and 'Solidity'.

• 'struct' is the only return type supported.

For more information, see Image Processing on a GPU.