Write Test Using Live Script
This example shows how to test a function by writing a live script named TestRightTriLiveScriptExample.mlx. The function returns the angles of a right triangle, and you create live-script-based unit tests to test this function. You can include equations and images in your live script to help document the test.
A live-script-based test follows these conventions:
The name of the test file must start or end with the word "test," which is case insensitive. If the filename does not start or end with "test," then the tests in the file might be ignored in certain cases.
Each unit test must be located in a separate section of the live script. If a section has a heading in the Heading 1 style, the heading becomes the name of the test. Otherwise, MATLAB® assigns a name to the test.
If you run the live script using the Run section on the Live Editor tab and MATLAB encounters a test failure, then it stops execution of the script and does not run any remaining tests. If you run the live script using the unit testing framework, for example, with the
runtestsfunction, and MATLAB encounters a test failure, it still runs the remaining tests.When a live script runs as a test, variables defined in one test are not accessible within other tests. Similarly, variables defined in other workspaces are not accessible to the tests.
Create Function to Test
In a file named rightTri.m in your current folder, create the rightTri function. The function takes the lengths of two sides of a triangle as an input and returns the three angles of the corresponding right triangle. The input sides are the two shorter edges of the triangle, not the hypotenuse.
type rightTri.mfunction angles = rightTri(sides) A = atand(sides(1)/sides(2)); B = atand(sides(2)/sides(1)); hypotenuse = sides(1)/sind(A); C = asind(hypotenuse*sind(A)/sides(1)); angles = [A B C]; end
Test: Small Angle Approximation

The rightTri function should return values consistent with the small angle approximation, such that . Create a test for the small angle approximation. Typically, when you compare floating-point values, you specify a tolerance for the comparison.
angles = rightTri([1 1500]); smallAngleInRadians = (pi/180)*angles(1); % Convert to radians approx = sin(smallAngleInRadians); assert(abs(approx-smallAngleInRadians) <= 1e-10,"Problem with small angle approximation")
Test: Sum of Angles
The sum of all angles of the resulting right triangle should be 180 degrees. Create a test for the sum of angles. You can have multiple assert statements in the same test. However, if an assertion fails, MATLAB does not evaluate the remaining statements.
angles = rightTri([7 9]); assert(sum(angles) == 180) angles = rightTri([4 4]); assert(sum(angles) == 180) angles = rightTri([2 2*sqrt(3)]); assert(sum(angles) == 180)
Test: 30-60-90 Triangle
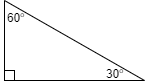
In a right triangle whose sides reduce to 1 and , the angles are . Create a test for this condition.
tol = 1e-10; angles = rightTri([2 2*sqrt(3)]); assert(abs(angles(1)-30) <= tol) assert(abs(angles(2)-60) <= tol) assert(abs(angles(3)-90) <= tol)
Test: Isosceles Triangles
In isosceles triangles, both of the non-right angles must be 45 degrees. Create a test for this condition.
angles = rightTri([4 4]); assert(angles(1) == 45) assert(angles(1) == angles(2))
Run Tests
To run the tests, you can use the runtests function in the unit testing framework or use the buttons in the Run section on the Live Editor tab. However, when you run a live script using the unit testing framework, the framework provides additional diagnostic information. In the event of a test failure, the framework runs subsequent tests, but the Run section buttons do not. For example, to run this test, enter result = runtests("TestRightTriLiveScriptExample") in the Command Window. For more information, see runtests.