erf
Error function
Syntax
Description
erf( returns the Error Function evaluated for each element
of x)x.
Examples
Input Arguments
More About
Tips
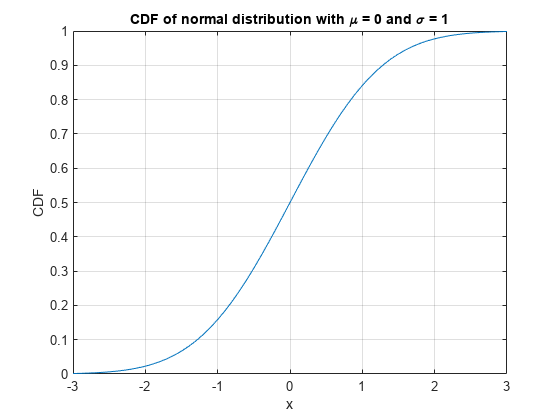
You can also find the standard normal probability distribution using the function
normcdf(Statistics and Machine Learning Toolbox). The relationship between the error functionerfandnormcdfisFor expressions of the form
1 - erf(x), use the complementary error functionerfcinstead. This substitution maintains accuracy. Whenerf(x)is close to1, then1 - erf(x)is a small number and might be rounded down to0. Instead, replace1 - erf(x)witherfc(x).
Extended Capabilities
Version History
Introduced before R2006a