erfinv
Inverse error function
Syntax
Description
erfinv( returns
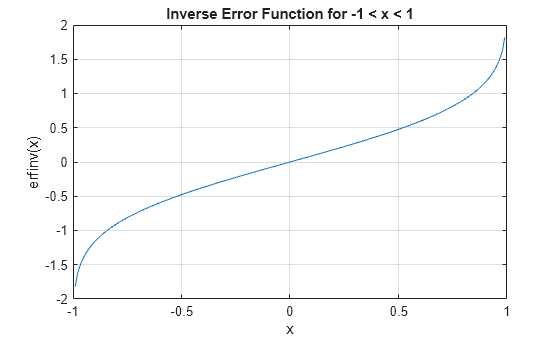
the Inverse Error Function evaluated
for each element of x)x. For inputs outside the
interval [-1 1], erfinv returns NaN.
Examples
Input Arguments
More About
Tips
For expressions of the form
erfinv(1-x), use the complementary inverse error functionerfcinvinstead. This substitution maintains accuracy. Whenxis close to1, then1 - xis a small number and may be rounded down to0. Instead, replaceerfinv(1-x)witherfcinv(x).
Extended Capabilities
Version History
Introduced before R2006a