degree
Degree of graph nodes
Description
Examples
Degree of All Graph Nodes
Create and plot a graph, and then use degree to find the degree of each node in the graph.
s = [1 1 1 4 4 6 6 6]; t = [2 3 4 5 6 7 8 9]; G = graph(s,t); plot(G)

deg = degree(G)
deg = 9×1
3
1
1
3
1
4
1
1
1
deg(j) indicates the degree of node j.
Degree of Subset of Graph Nodes
Create and plot a graph, and then find the degree of the first, third, and fifth nodes.
s = {'a' 'a' 'a' 'd' 'd' 'f' 'f' 'f'};
t = {'b' 'c' 'd' 'e' 'f' 'g' 'h' 'i'};
G = graph(s,t);
plot(G)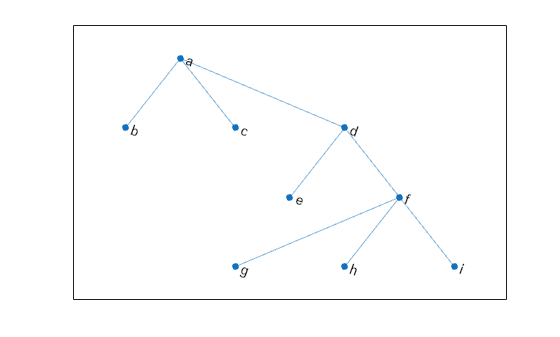
nodeIDs = {'a' 'c' 'e'}';
deg = degree(G,nodeIDs)deg = 3×1
3
1
1
deg(j) indicates the degree of node nodeIDs(j).
Input Arguments
G — Input graph
graph object
Input graph, specified as a graph object. Use graph to create an undirected graph object.
Example: G = graph(1,2)
nodeIDs — Node identifiers
node indices | node names
Node identifiers, specified as one or more node indices or node names.
This table shows the different ways to refer to one or more nodes either by their numeric node indices or by their node names.
| Form | Single Node | Multiple Nodes |
|---|---|---|
| Node index | Scalar Example: | Vector Example: |
| Node name | Character vector Example: | Cell array of character vectors Example: |
String scalar Example: | String array Example: |
Example: D = degree(G,[3 4])
Example: D = degree(G,{'LAX','ALB'})
Output Arguments
D — Degree of nodes
array
Degree of nodes, returned as a numeric array. D is a
column vector unless you specify nodeIDs, in which case
D has the same size as
nodeIDs.
A node that is connected to itself by an edge (a self-loop) is listed as its own neighbor only once, but the self-loop adds 2 to the total degree of the node.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
The node identifiers
nodeIDsmust be one or more node indices of the input graphG. Node names are not supported.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2015b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)