graph
Graph with undirected edges
Description
graph objects represent undirected graphs, which have
direction-less edges connecting the nodes. After you create a graph object, you can
learn more about the graph by using object functions to perform queries against the
object. For example, you can add or remove nodes or edges, determine the shortest path
between two nodes, or locate a specific node or edge.
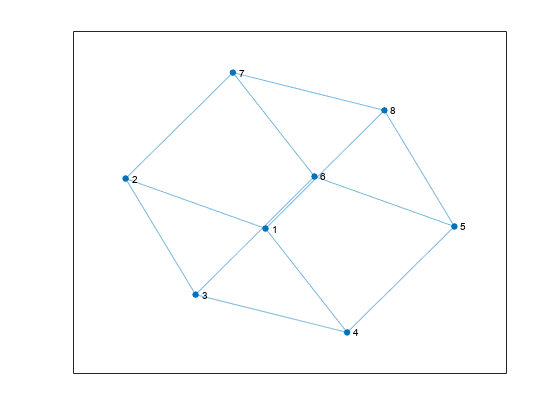
G = graph([1 1], [2 3]); e = G.Edges G = addedge(G,2,3) G = addnode(G,4) plot(G)
Creation
Syntax
Description
G = graphG, which has no nodes or
edges.
G = graph(A)A.
For logical adjacency matrices, the graph has no edge weights.
For nonlogical adjacency matrices, the graph has edge weights. The location of each nonzero entry in
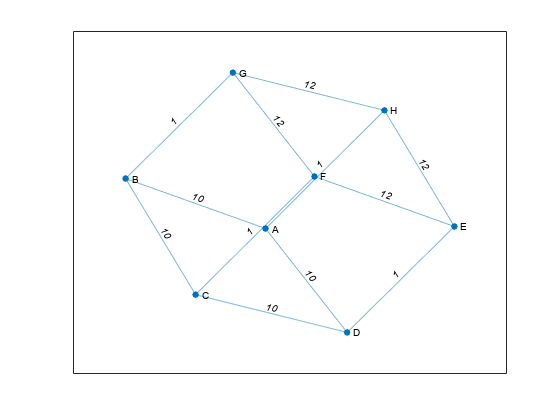
Aspecifies an edge for the graph, and the weight of the edge is equal to the value of the entry. For example, ifA(2,1) = 10, thenGcontains an edge between node 2 and node 1 with a weight of 10.
G = graph(s,t)(s,t) in node pairs.
s and t can specify node indices
or node names. graph sorts the edges in
G first by source node, and then by target node. If
you have edge properties that are in the same order as s
and t, use the syntax G =
graph(s,t,EdgeTable) to pass in the edge properties so that
they are sorted in the same manner in the resulting graph.
G = graph(s,t,___,'omitselfloops')k
that satisfies s(k) == t(k) is ignored. You can use any
of the input argument combinations in previous syntaxes.
G = graph(EdgeTable)EdgeTable to define the graph. With this
syntax, the first variable in EdgeTable must be named
EndNodes, and it must be a two-column array defining
the edge list of the graph.
G = graph(EdgeTable,___,'omitselfloops')k that
satisfies EdgeTable.EndNodes(k,1) ==
EdgeTable.EndNodes(k,2) is ignored. You must specify
EdgeTable and optionally can specify
NodeTable.