bctree
Block-cut tree graph
Description
tree = bctree(G)G, such that each node in
tree represents either a biconnected component or cut
vertex of G. A node representing a cut vertex is
connected to all nodes representing biconnected components that contain that cut
vertex.
Examples
Compute the block-cut tree of a graph, view the resulting node properties, and then highlight the cut vertices in the graph plot.
Create and plot a graph.
s = [1 1 2 2 3 4 4 5 6 6 7 7 8]; t = [2 3 3 4 4 5 7 6 7 10 8 9 9]; G = graph(s,t); p = plot(G);
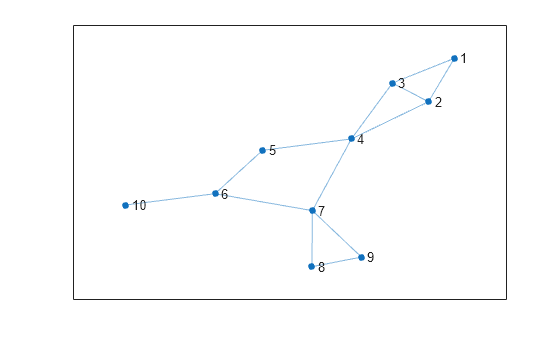
Compute the block-cut tree of the graph and view the node properties.
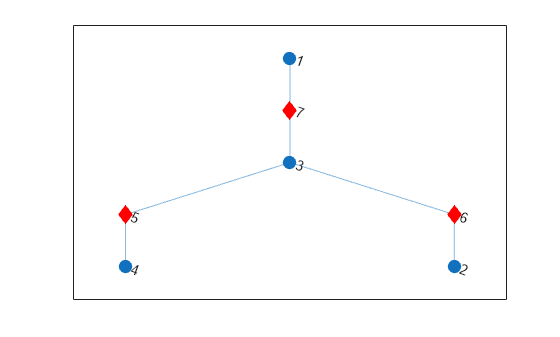
tree = bctree(G); tree.Nodes
ans=7×3 table
IsComponent ComponentIndex CutVertexIndex
___________ ______________ ______________
true 1 0
true 2 0
true 3 0
true 4 0
false 0 4
false 0 6
false 0 7
Plot the block-cut tree using red diamond markers for the nodes that represent cut vertices. The circular nodes represent the biconnected components in the original graph.
p2 = plot(tree,'MarkerSize',9); highlight(p2,5:7,'Marker','d','NodeColor','r')
Create and plot a graph.
s = [1 1 2 2 3 4 4 5 6 6 7 7 8]; t = [2 3 3 4 4 5 7 6 7 10 8 9 9]; G = graph(s,t); p = plot(G);
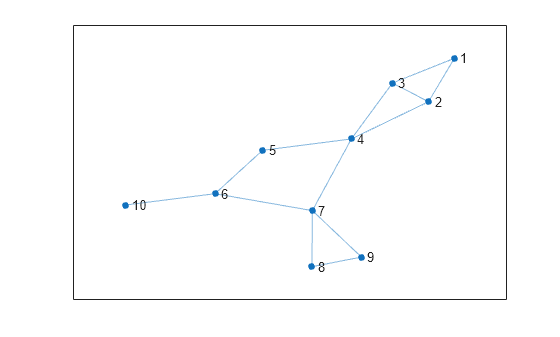
Compute the block-cut tree tr of the graph, and specify a second output ix to return the node indices.
[tr,ix] = bctree(G)
tr =
graph with properties:
Edges: [6×1 table]
Nodes: [7×3 table]
ix = 1×10
4 4 4 5 3 6 7 1 1 2
Each index ix(j) indicates the node in the block-cut tree that represents node j in the input graph. For example, node 4 in tr represents a component in G that contains nodes 1, 2, and 3, so the first three entries in ix are all 4.
Input Arguments
Input graph, specified as a graph object. Use graph to create an undirected graph object.
Example: G = graph(1,2)
Output Arguments
Block-cut tree graph, returned as a graph object.
tree contains a node for each cut vertex in
G and a node for each biconnected component in
G. The nodes table tree.Nodes
contains additional node attributes to describe what each node
represents:
tree.Nodes.IsComponent(i)— Value equal to logical1(true) if nodeirepresents a biconnected component. Otherwise, the value is equal to and logical0(false).tree.Nodes.ComponentIndex(i)— Index indicating the component represented by nodei. The value is zero if nodeirepresents a cut vertex.tree.Nodes.CutVertexIndex(i)— Index indicating the cut vertex represented by nodei. The value is zero if nodeirepresents a biconnected component.
Node indices, returned as a numeric vector. ind(i) is
the node in the output graph tree that represents node
i in the input graph G:
If node
iis a cut vertex in graphG, thenind(i)is the associated node intree.If node
iis not a cut vertex, but belongs to one of the biconnected components in graphG, thenind(i)is the node intreerepresenting that biconnected component.If node
iis an isolated node in graphG, thenind(i)is zero.
More About
A biconnected component of a graph is a maximally biconnected subgraph. A graph is biconnected if it does not contain any cut vertices.
Decomposing a graph into its biconnected components helps to measure how well-connected the graph is. You can decompose any connected graph into a tree of biconnected components, called the block-cut tree. The blocks in the tree are attached at shared vertices, which are the cut vertices.
The illustration depicts:
(a) An undirected graph with 11 nodes.
(b) Five biconnected components of the graph, with the cut vertices of the original graph colored for each component to which they belong.
(c) Block-cut tree of the graph, which contains a node for each biconnected component (as large circles) and a node for each cut vertex (as smaller multicolored circles). In the block-cut tree, an edge connects each cut vertex to each component to which it belongs.
![]()
Also known as articulation points, cut vertices are graph nodes whose removal increases the number of connected components. In the previous illustration, the cut vertices are those nodes with more than one color: nodes 4, 6, and 7.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2016b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)