interpn
Interpolation for 1-D, 2-D, 3-D, and N-D gridded data in ndgrid format
Syntax
Description
Vq = interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn)X1,X2,...,Xn contain
the coordinates of the sample points. V contains
the corresponding function values at each sample point. Xq1,Xq2,...,Xqn contain
the coordinates of the query points.
Vq = interpn(V,Xq1,Xq2,...,Xqn)V. Use this syntax when you want to conserve memory and
are not concerned about the absolute distances between points.
Vq = interpn(___,method,extrapval)extrapval, a scalar value that is assigned
to all queries that lie outside the domain of the sample points.
If you omit the extrapval argument for queries
outside the domain of the sample points, then based on the method argument interpn returns
one of the following:
The extrapolated values for the
'spline'and'makima'methodsNaNvalues for other interpolation methods
Examples
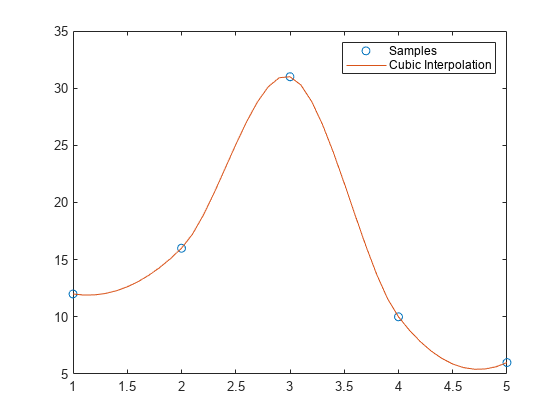
Define the sample points and values.
x = [1 2 3 4 5]; v = [12 16 31 10 6];
Define the query points, xq, and interpolate.
xq = (1:0.1:5);
vq = interpn(x,v,xq,'cubic');Plot the result.
figure plot(x,v,'o',xq,vq,'-'); legend('Samples','Cubic Interpolation');
Create a set of grid points and corresponding sample values.
[X1,X2] = ndgrid((-5:1:5)); R = sqrt(X1.^2 + X2.^2)+ eps; V = sin(R)./(R);
Interpolate over a finer grid using ntimes=1.
Vq = interpn(V,'cubic');
mesh(Vq);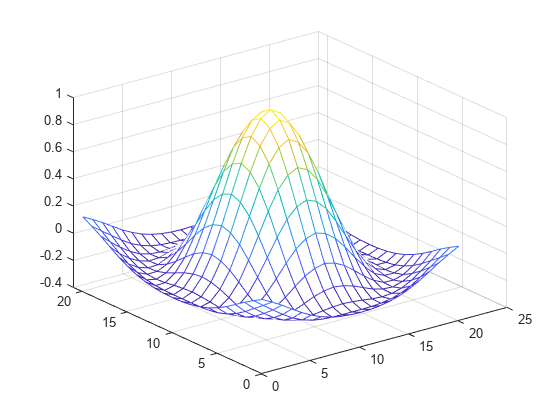
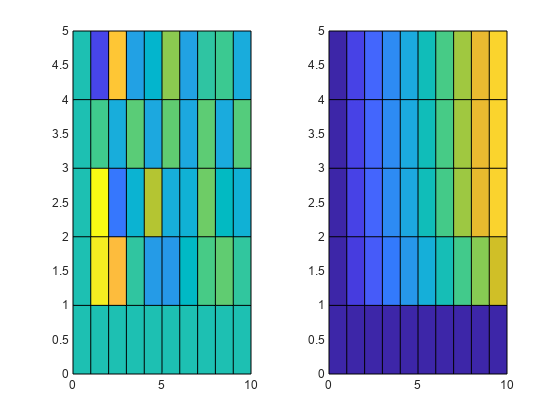
Create a grid of 2-D sample points using ndgrid.
[x,y] = ndgrid(0:10,0:5);
Create two different sets of sample values at the sample points and concatenate them as pages in a 3-D array. Plot the two sets of sample values against the sample points. Because surf uses meshgrid format for grids, transpose the inputs for plotting.
v1 = sin(x.*y)./(x+1); v2 = x.*erf(y); V = cat(3,v1,v2); tiledlayout(1,2) nexttile surf(x',y',V(:,:,1)') view(2) nexttile surf(x',y',V(:,:,2)') view(2)
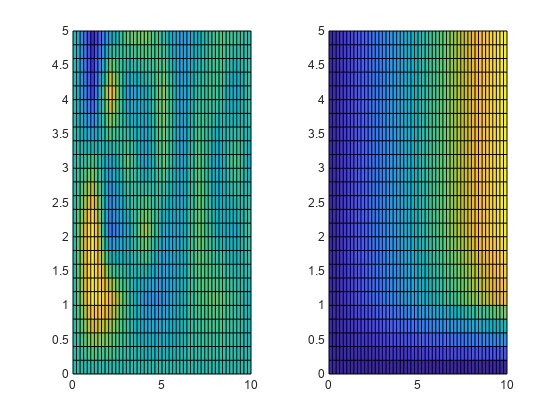
Create a set of query points for interpolation using ndgrid and then use interpn to find the values of each function at the query points. Plot the interpolated values against the query points.
[xq,yq] = ndgrid(0:0.2:10); Vq = interpn(x,y,V,xq,yq); tiledlayout(1,2) nexttile surf(xq',yq',Vq(:,:,1)') view(2) nexttile surf(xq',yq',Vq(:,:,2)') view(2)
Create the grid vectors, x1, x2, and x3. These vectors define the points associated with the values in V.
x1 = 1:100; x2 = 1:50; x3 = 1:30;
Define the sample values to be a 100-by-50-by-30 array of random numbers, V.
rng default
V = rand(100,50,30);Evaluate V at three points outside the domain of x1, x2, and x3. Specify extrapval = -1.
xq1 = [0 0 0];
xq2 = [0 0 51];
xq3 = [0 101 102];
vq = interpn(x1,x2,x3,V,xq1,xq2,xq3,'linear',-1)vq = 1×3
-1 -1 -1
All three points evaluate to -1 because they are outside the domain of x1, x2, and x3.
Define an anonymous function that represents 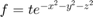 .
.
f = @(x,y,z,t) t.*exp(-x.^2 - y.^2 - z.^2);
Create a grid of points in 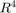 . Then, pass the points through the function to create the sample values,
. Then, pass the points through the function to create the sample values, V.
[x,y,z,t] = ndgrid(-1:0.2:1,-1:0.2:1,-1:0.2:1,0:2:10); V = f(x,y,z,t);
Now, create the query grid.
[xq,yq,zq,tq] = ...
ndgrid(-1:0.05:1,-1:0.08:1,-1:0.05:1,0:0.5:10);
Interpolate V at the query points.
Vq = interpn(x,y,z,t,V,xq,yq,zq,tq);
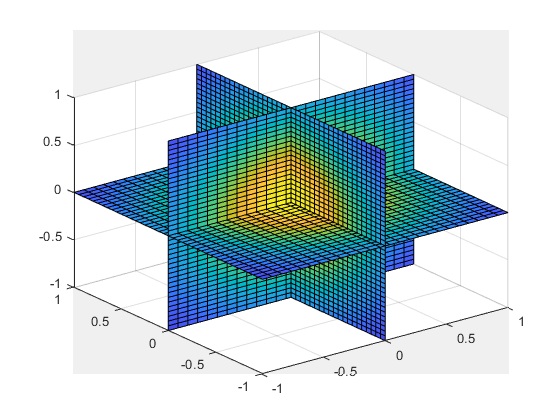
Create a movie to show the results.
figure; nframes = size(tq, 4); for j = 1:nframes slice(yq(:,:,:,j),xq(:,:,:,j),zq(:,:,:,j),... Vq(:,:,:,j),0,0,0); clim([0 10]); M(j) = getframe; end movie(M);
Input Arguments
Sample grid points, specified as real arrays or vectors. The sample grid points must be unique.
If
X1,X2,...,Xnare arrays, then they contain the coordinates of a full grid (in ndgrid format). Use thendgridfunction to create theX1,X2,...,Xnarrays together. These arrays must be the same size.If
X1,X2,...,Xnare vectors, then they are treated as grid vectors. The values in these vectors must be strictly monotonic, either increasing or decreasing.
Example: [X1,X2,X3,X4] = ndgrid(1:30,-10:10,1:5,10:13)
Data Types: single | double
Sample values, specified as a real or complex array. The size requirements for
V depend on the size of the grid of sample points
defined by X1,X2,...,Xn. The sample points
X1,X2,...,Xn can be arrays or grid vectors, but in
both cases they define an n-dimensional grid.
V must be an array that at least has the same
n dimension sizes, but it also can have extra
dimensions beyond n:
If
Valso hasndimensions, then the size ofVmust match the size of the n-dimensional grid defined byX1,X2,...,Xn. In this case,Vcontains one set of sample values at the sample points. For example, ifX1,X2,X3are 3-by-3-by-3 arrays, thenVcan also be a 3-by-3-by-3 array.If
Vhas more thanndimensions, then the firstndimensions ofVmust match the size of the n-dimensional grid defined byX1,X2,...,Xn. The extra dimensions inVdefine extra sets of sample values at the sample points. For example, ifX1,X2,X3are 3-by-3-by-3 arrays, thenVcan be a 3-by-3-by-3-by-2 array to define two sets of sample values at the sample points.
If V contains complex numbers, then interpn interpolates
the real and imaginary parts separately.
Example: rand(10,5,3,2)
Data Types: single | double
Complex Number Support: Yes
Query points, specified as real scalars, vectors, or arrays.
If
Xq1,Xq2,...,Xqnare scalars, then they are the coordinates of a single query point in Rn.If
Xq1,Xq2,...,Xqnare vectors of different orientations, thenXq1,Xq2,...,Xqnare treated as grid vectors in Rn.If
Xq1,Xq2,...,Xqnare vectors of the same size and orientation, thenXq1,Xq2,...,Xqnare treated as scattered points in Rn.If
Xq1,Xq2,...,Xqnare arrays of the same size, then they represent either a full grid of query points (inndgridformat) or scattered points in Rn.
Example: [X1,X2,X3,X4] = ndgrid(1:10,1:5,7:9,10:11)
Data Types: single | double
Refinement factor, specified as a real, nonnegative, integer
scalar. This value specifies the number of times to repeatedly divide
the intervals of the refined grid in each dimension. This results
in 2^k-1 interpolated points between sample values.
If k is 0, then Vq is
the same as V.
interpn(V,1) is the same as interpn(V).
The following illustration depicts k=2 in R2.
There are 72 interpolated values in red and 9 sample values in black.

Example: interpn(V,2)
Data Types: single | double
Interpolation method, specified as one of the options in this table.
| Method | Description | Continuity | Comments |
|---|---|---|---|
'linear' | The interpolated value at a query point is based on linear interpolation of the values at neighboring grid points in each respective dimension. This is the default interpolation method. | C0 |
|
'nearest' | The interpolated value at a query point is the value at the nearest sample grid point. | Discontinuous |
|
'pchip' | Shape-preserving piecewise cubic interpolation (for 1-D only). The interpolated value at a query point is based on a shape-preserving piecewise cubic interpolation of the values at neighboring grid points. | C1 |
|
'cubic' | The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic convolution. | C1 |
|
'makima' | Modified Akima cubic Hermite interpolation. The interpolated value at a query point is based on a piecewise function of polynomials with degree at most three evaluated using the values of neighboring grid points in each respective dimension. The Akima formula is modified to avoid overshoots. | C1 |
|
'spline' | The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic spline using not-a-knot end conditions. | C2 |
|
Function value outside domain of X1,X2,...,Xn,
specified as a real or complex scalar. interpn returns
this constant value for all points outside the domain of X1,X2,...,Xn.
Example: 5
Example: 5+1i
Data Types: single | double
Complex Number Support: Yes
Output Arguments
Interpolated values, returned as a real or complex scalar, vector, or array. The size and
shape of Vq depends on the syntax you use and, in some
cases, the size and value of the input arguments.
If you specify sample points with
X1,X2,...,Xn, or use the default grid, andVhas the same number of dimensions as the n-dimensional grid of sample points, thenVqcontains a single set of interpolated values at the query points defined byXq1,Xq2,...,Xqn.If
Xq1,Xq2,...,Xqnare scalars, thenVqis a scalar.If
Xq1,Xq2,...,Xqnare vectors of the same size and orientation, thenVqis a vector with the same size and orientation.If
Xq1,Xq2,...,Xqnare grid vectors of mixed orientation, thenVqis an array with the same size as the grid implicitly defined by the grid vectors.If
Xq1,Xq2,...,Xqnare arrays of the same size, thenVqis an array with the same size.
If you specify sample points with
X1,X2,...,Xn, or use the default grid, andVhas more dimensions than the n-dimensional grid of sample points, thenVqcontains multiple sets of interpolated values at the query points defined byXq1,Xq2,...,Xqn. In this case, the first n dimensions ofVqfollow the size rules for a single set of interpolated values above, butVqalso has the same extra dimensions asVwith the same sizes.With the syntaxes
interpn(V)andinterpn(V,k), the interpolation is performed by subdividing the default gridktimes (wherek=1forinterpn(V)). In this case,Vqis an array with the same number of dimensions asVwhere the size of the ith dimension is2^k * (size(V,i)-1)+1.
More About
A set of values that are always increasing
or decreasing, without reversals. For example, the sequence, a
= [2 4 6 8] is strictly monotonic and increasing. The sequence, b
= [2 4 4 6 8] is not strictly monotonic because there is
no change in value between b(2) and b(3).
The sequence, c = [2 4 6 8 6] contains a reversal
between c(4) and c(5), so it
is not monotonic at all.
For interpn, the full
grid consists of n arrays, X1,X2,...,Xn,
whose elements represent a grid of points in Rn.
The ith array, Xi, contains strictly monotonic,
increasing values that vary most rapidly along the ith dimension.
Use the ndgrid function
to create a full grid that you can pass to interpn.
For example, the following code creates a full grid in R2 for
the region, 1 ≤ X1 ≤ 3, 1≤ X2 ≤
4.
[X1,X2] = ndgrid(-1:3,(1:4))
X1 =
-1 -1 -1 -1
0 0 0 0
1 1 1 1
2 2 2 2
3 3 3 3
X2 =
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4For interpn, grid vectors
consist of n vectors of mixed-orientation that
define the points of a grid in Rn.
For example, the following code creates the grid vectors in R3 for the region, 1 ≤ x1 ≤ 3, 4 ≤ x2 ≤ 5, and 6 ≤x3≤ 8:
x1 = 1:3; x2 = (4:5)'; x3 = 6:8;
For interpn, scattered
points consist of n arrays or vectors, Xq1,Xq2,...,Xqn,
that define a collection of points scattered in Rn.
The ith array, Xi, contains
the coordinates in the ith dimension.
For example, the following code specifies the points, (1, 19, 10), (6, 40, 1), (15, 33, 22), and (0, 61, 13) in R3.
Xq1 = [1 6; 15 0]; Xq2 = [19 40; 33 61]; Xq3 = [10 1; 22 13];
Extended Capabilities
Usage notes and limitations:
For best results, provide
X1,X2,...,Xnas vectors. The values in these vectors must be strictly monotonic and increasing.Code generation does not support the
'makima'interpolation method.The interpolation method must be a constant character vector.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The interpn function
supports GPU array input with these usage notes and limitations:
A maximum of five dimensions is supported.
X1,X2,...,Xnmust have dimensions consistent withV.methodmust be'linear'or'nearest'.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Usage notes and limitations:
X1,X2,...,Xnmust have dimensions consistent withV.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006aSupport added to interpolate multiple data sets on the same grid at the same query
points. For example, if you specify a 2-D grid, a 3-D array of values at the grid
points, and a 2-D collection of query points, then interpn
returns the interpolated values at the query points for each 2-D page in the 3-D
array of values.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)