matchpairs
Solve linear assignment problem
Syntax
Description
M = matchpairs(Cost,costUnmatched)Cost. Each row is
assigned to a column in such a way that the total cost is minimized.
costUnmatched specifies the cost per row of not assigning each row, and
also the cost per column of not having a row assigned to each column.
[
additionally returns indices for unmatched rows in M,uR,uC] = matchpairs(Cost,costUnmatched)uR and indices for
unmatched columns in uC.
[___] = matchpairs(
specifies the goal of the optimization using any of the output argument combinations in
previous syntaxes. Cost,costUnmatched,goal)goal can be 'min' or
'max' to produce matches that either minimize or maximize the total
cost.
Examples
Assign salespeople to flights such that the total cost of transportation is minimized.
A company has four salespeople who need to travel to key cities around the country. The company must book their flights, and wants to spend as little money as possible. These salespeople are based in different parts of the country, so the cost for them to fly to each city varies.
This table shows the cost for each salesperson to fly to each key city.
Each city represents a sales opportunity. If a city is missed, then the company loses out on an average revenue gain of $2,000.
Create a cost matrix to represent the cost of each salesperson flying to each city.
C = [600 670 960 560
900 280 970 540
310 350 950 820
325 290 600 540];Use matchpairs to assign the salespeople to the cities with minimal cost. Specify the cost of unassignment as 1000, since the cost of unassignment is counted twice if a row and a column remain unmatched.
M = matchpairs(C,1000)
M = 4×2
3 1
2 2
4 3
1 4
matchpairs calculates the least expensive way to get a salesperson to each city.
Match rows to columns when you have many more columns than rows in the cost matrix.
Create a 3-by-8 cost matrix. Since you have only three rows, matchpairs can produce at most three matches with the eight columns.
rng default % for reproducibility C = randi([10 100], 3, 8)
C = 3×8
84 93 35 97 97 22 82 13
92 67 59 24 54 48 97 87
21 18 97 98 82 93 69 94
Use matchpairs to match the rows and columns of the cost matrix. To get the maximum number of matches, use a large cost of unassignment (relative to the magnitude of the entries in the cost matrix). Specify three outputs to return the indices of unmatched rows and columns.
[M,uR,uC] = matchpairs(C,1e4)
M = 3×2
3 2
2 4
1 8
uR = 0×1 empty double column vector
uC = 5×1
1
3
5
6
7
Five of the columns in C are not matched with any rows.
Assign taxis to routes such that the profit is maximized.
A taxi company has several ride requests from across the city. The company wants to dispatch its limited number of taxis in a way that makes the most money.
This table shows the estimated taxi fare for each of five ride requests. Only three of the five ride requests can be filled.
Create a profits matrix to represent the profits of each taxi ride.
P = [5.7 6.3 3.1 4.8 3.5
5.8 6.4 3.3 4.7 3.2
5.7 6.3 3.2 4.9 3.4];Use matchpairs to match the taxis to the most profitable rides. Specify three outputs to return any unmatched rows and columns, and the 'max' option to maximize the profits. Specify the cost of unassignment as zero, since the company makes no money from unfilled taxis or ride requests.
costUnmatched = 0;
[M,uR,uC] = matchpairs(P,costUnmatched,'max')M = 3×2
1 1
2 2
3 4
uR = 0×1 empty double column vector
uC = 2×1
3
5
matchpairs calculates the most profitable rides to fill. The solution leaves ride requests 3 and 5 unfilled.
Calculate the total profits for the calculated solution. Since costUnmatched is zero, you only need to add together the profits from each match.
TotalProfits = sum(P(sub2ind(size(P), M(:,1), M(:,2))))
TotalProfits = 17
Use matchpairs to track the movement of several points by minimizing the total changes in distance.
Plot a grid of points at time in green. At time , some of the points move a small amount in a random direction.
[x,y] = meshgrid(4:6:16); x0 = x(:)'; y0 = y(:)'; plot(x0,y0,'g*') hold on rng default % for reproducibility x1 = x0 + randn(size(x0)); y1 = y0 + randn(size(y0)); plot(x1,y1,'r*')
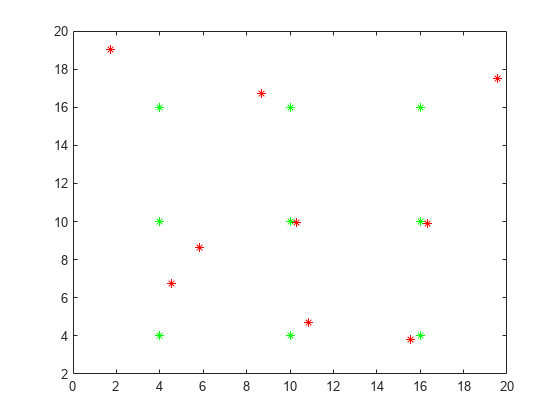
Use matchpairs to match the points at with the points at . To do this, first calculate a cost matrix where C(i,j) is the Euclidean distance from point i to point j.
C = zeros(size(x).^2); for k = 1:length(y1) C(k,:) = vecnorm([x1(k)-x0; y1(k)-y0],2,1)'; end C
C = 9×9
2.8211 3.2750 9.2462 6.1243 6.3461 10.7257 11.7922 11.9089 14.7169
4.9987 2.2771 7.5752 6.2434 4.3794 8.4485 11.1792 10.2553 12.5447
15.2037 9.3130 3.7833 17.1539 12.2408 8.7988 20.7211 16.8803 14.5783
6.9004 8.6551 13.1987 1.1267 5.3446 11.3075 5.1888 7.3633 12.3901
8.6703 6.3191 8.7571 5.9455 0.3249 6.0714 8.2173 5.6816 8.3089
13.5530 8.1918 4.7464 12.7818 6.8409 1.4903 14.6652 9.9242 7.3426
11.5682 13.1257 16.8150 5.5702 8.3359 13.4144 0.4796 6.2201 12.2127
13.6699 12.3432 13.7784 8.6461 6.3438 8.8167 5.8858 0.3644 6.1337
20.6072 17.2853 15.6495 16.5444 12.1590 9.6935 13.9562 8.3006 3.8761
Next, use matchpairs to match the rows and columns in the cost matrix. Specify the cost of unassignment as 1. With such a low cost of unassignment relative to the entries in the cost matrix, it is likely matchpairs will leave some points unmatched.
M = matchpairs(C,1)
M = 5×2
4 4
5 5
6 6
7 7
8 8
The values M(:,2) correspond to the original points , while the values M(:,1) correspond to the moved points .
Plot the matched pairs of points. The points that moved farther than 2*costUnmatched away from the original point remain unmatched.
xc = [x0(M(:,2)); x1(M(:,1))];
yc = [y0(M(:,2)); y1(M(:,1))];
plot(xc,yc,'-o')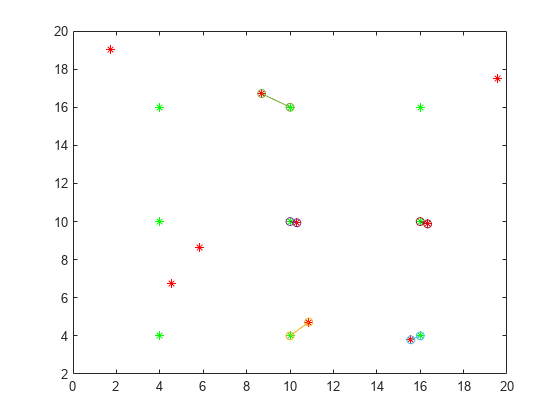
Input Arguments
Cost matrix. Each entry Cost(i,j) specifies the cost of assigning
row i to column j.
Data Types: single | double
Cost of not matching, specified as a scalar. matchpairs
compares the value of 2*costUnmatched to the entries in
Cost to determine whether it is more beneficial for a row or
column to remain unmatched. Use this parameter to make matches more or less likely in
the algorithm. For more information, see linear assignment
problem.
Example: M = matchpairs(C,10) specifies a cost of 10 for not
matching a row or column of C.
Data Types: single | double
Optimization goal, specified as either 'min' or
'max'. The optimization goal specifies whether the total cost
should be minimized or maximized.
Example: M = matchpairs(Cost,costUnmatched,'max') specifies that
the rows and columns of Cost should be matched together to maximize
the total cost.
Output Arguments
Matches, returned as a matrix. M is a
p-by-2 matrix, where M(i,1)
and M(i,2) are the row and column indices of a matched pair in the
cost matrix. The rows of M are sorted with the second column in
ascending order.
Each row and column can be matched a single time only, so each
M(i,1)value and eachM(i,2)value is unique.Mcontainspmatches, andpis less than or equal to the maximum number of matchesmin(size(Cost)).The cost of the matches in
Missum([Cost(M(1,1),M(1,2)), Cost(M(2,1),M(2,2)), ..., Cost(M(p,1),M(p,2))]).
Unassigned rows, returned as a column vector of indices. The entries in
uR indicate which rows in Cost are unassigned.
Each entry in uR and uC contributes to the total
cost of the solution according to costUnassigned.
Unassigned columns, returned as a column vector of indices. The entries in
uC indicate which columns in Cost are
unassigned. Each entry in uR and uC contributes to
the total cost of the solution according to costUnassigned.
More About
The linear assignment problem is a way of
assigning rows to columns such that each row is assigned to a column and the total cost of
the assignments is minimized (or maximized). The cost of assigning each row to each column
is captured in a cost matrix. The entry Cost(i,j) is
the cost of assigning row i to column j.
The cost of unassignment assigns a cost to any row or column that
is not matched. This practice allows for minimum-cost solutions that do not assign all rows
or columns. If a row and column are not matched, this increases the total cost by
2*costUnmatched.
The total cost of a solution M is the sum of the cost of all matched
pairs added to the cost of all unmatched pairs:
In code the total cost is
CostAssigned = sum(Cost(sub2ind(size(Cost), M(:,1), M(:,2)))); CostUnassigned = costUnmatched*(sum(size(Cost))-2*size(M,1)); TotalCost = CostAssigned + CostUnassigned;
Costis anm-by-nmatrix.Mis ap-by-2matrix, whereM(i,1)andM(i,2)are the row and column of a matched pair.(m+n-2*p)is the total number of unmatched rows and columns.
References
[1] Duff, I.S. and J. Koster. "On Algorithms For Permuting Large Entries to the Diagonal of a Sparse Matrix." SIAM J. Matrix Anal. & Appl. 22(4), 2001. pp 973–996.
Extended Capabilities
Usage notes and limitations:
Code generation does not support sparse matrix inputs for this function.
Version History
Introduced in R2019a
See Also
equilibrate | sprank | dmperm
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)