pchip
Piecewise Cubic Hermite Interpolating Polynomial (PCHIP)
Description
p = pchip(x,y,xq)p corresponding
to the query points in xq. The values of p are
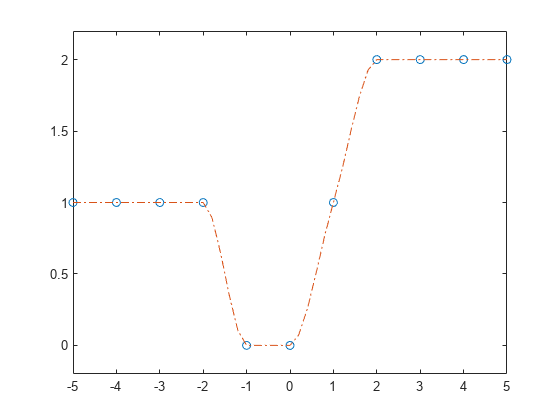
determined by shape-preserving piecewise cubic
interpolation of x and y.
Examples
Input Arguments
Output Arguments
More About
Tips
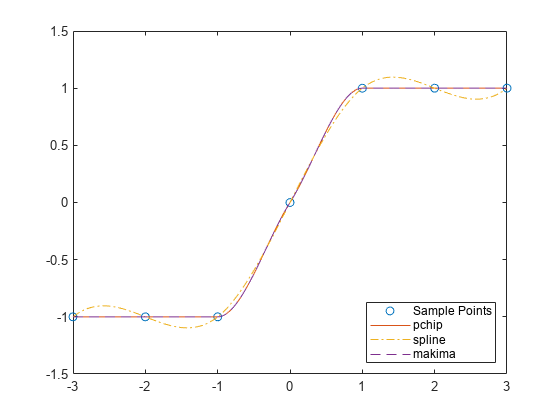
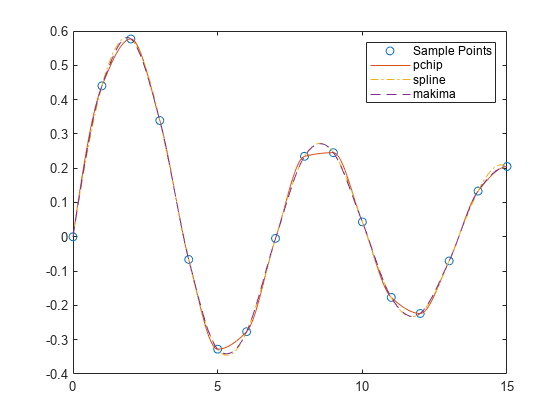
splineconstructs in almost the same waypchipconstructs . However,splinechooses the slopes at the differently, namely to make even continuous. This difference has several effects:splineproduces a smoother result, such that is continuous.splineproduces a more accurate result if the data consists of values of a smooth function.pchiphas no overshoots and less oscillation if the data is not smooth.pchipis less expensive to set up.The two are equally expensive to evaluate.
References
[1] Fritsch, F. N. and R. E. Carlson. "Monotone Piecewise Cubic Interpolation." SIAM Journal on Numerical Analysis. Vol. 17, 1980, pp.238–246.
[2] Kahaner, David, Cleve Moler, Stephen Nash. Numerical Methods and Software. Upper Saddle River, NJ: Prentice Hall, 1988.
Extended Capabilities
Version History
Introduced before R2006a