plot
2-D line plot
Syntax
Description
Vector and Matrix Data
plot( plots Y)Y
against an implicit set of x-coordinates.
If
Yis a vector, the x-coordinates range from 1 tolength(Y).If
Yis a matrix, the plot contains one line for each column inY. The x-coordinates range from 1 to the number of rows inY.
If Y contains complex numbers, MATLAB® plots the imaginary part of Y versus the real
part of Y. If you specify both X and
Y, the imaginary part is ignored.
Table Data
plot(
plots the variables tbl,xvar,yvar)xvar and yvar from the
table tbl. To plot one data set, specify one variable for
xvar and one variable for yvar. To
plot multiple data sets, specify multiple variables for xvar,
yvar, or both. If both arguments specify multiple
variables, they must specify the same number of variables. (since R2022a)
Additional Options
plot( displays
the plot in the target axes. Specify the axes as the first argument in any of
the previous syntaxes.ax,___)
plot(___,
specifies Name,Value)Line properties using one or more name-value
arguments. The properties apply to all the plotted lines. Specify the name-value
arguments after all the arguments in any of the previous syntaxes. For a list of
properties, see Line Properties.
p = plot(___) returns a
Line object or an array of Line
objects. Use p to modify properties of the plot after
creating it. For a list of properties, see Line Properties.
Examples
Create x as a vector of linearly spaced values between 0 and . Use an increment of between the values. Create y as sine values of x. Create a line plot of the data.
x = 0:pi/100:2*pi; y = sin(x); plot(x,y)
Define x as 100 linearly spaced values between and . Define y1 and y2 as sine and cosine values of x. Create a line plot of both sets of data.
x = linspace(-2*pi,2*pi); y1 = sin(x); y2 = cos(x); figure plot(x,y1,x,y2)
Define Y as the 4-by-4 matrix returned by the magic function.
Y = magic(4)
Y = 4×4
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Create a 2-D line plot of Y. MATLAB® plots each matrix column as a separate line.
figure plot(Y)
Plot three sine curves with a small phase shift between each line. Use the default line style for the first line. Specify a dashed line style for the second line and a dotted line style for the third line.
x = 0:pi/100:2*pi; y1 = sin(x); y2 = sin(x-0.25); y3 = sin(x-0.5); figure plot(x,y1,x,y2,'--',x,y3,':')
MATLAB® cycles the line color through the default color order.
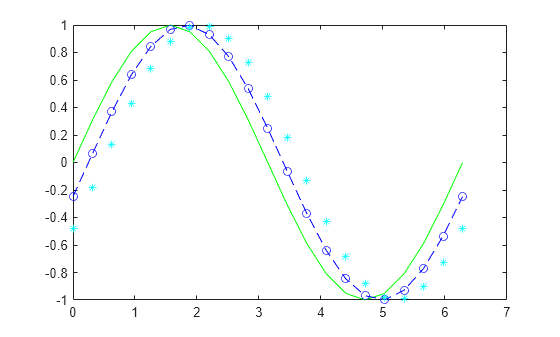
Plot three sine curves with a small phase shift between each line. Use a green line with no markers for the first sine curve. Use a blue dashed line with circle markers for the second sine curve. Use only cyan star markers for the third sine curve.
x = 0:pi/10:2*pi; y1 = sin(x); y2 = sin(x-0.25); y3 = sin(x-0.5); figure plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')
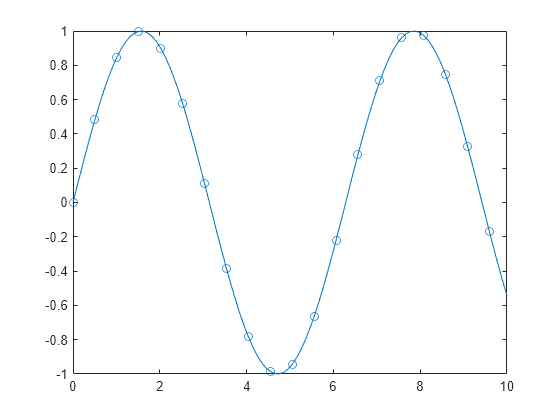
Create a line plot and display markers at every fifth data point by specifying a marker symbol and setting the MarkerIndices property as a name-value pair.
x = linspace(0,10); y = sin(x); plot(x,y,'-o','MarkerIndices',1:5:length(y))
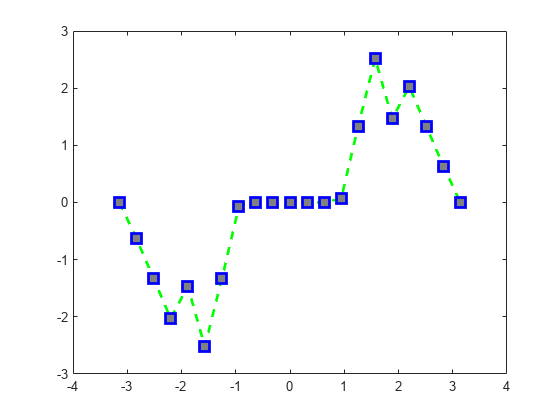
Create a line plot and use the LineSpec option to specify a dashed green line with square markers. Use Name,Value pairs to specify the line width, marker size, and marker colors. Set the marker edge color to blue and set the marker face color using an RGB color value.
x = -pi:pi/10:pi; y = tan(sin(x)) - sin(tan(x)); figure plot(x,y,'--gs',... 'LineWidth',2,... 'MarkerSize',10,... 'MarkerEdgeColor','b',... 'MarkerFaceColor',[0.5,0.5,0.5])
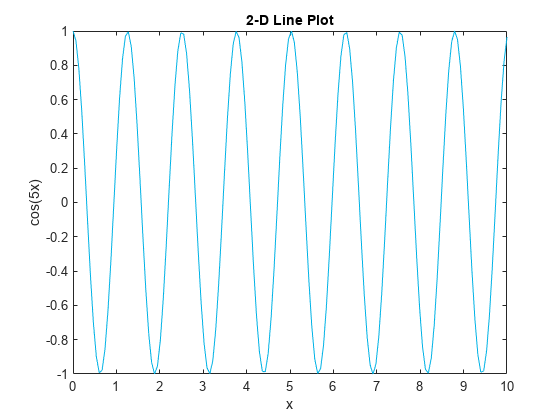
Use the linspace function to define x as a vector of 150 values between 0 and 10. Define y as cosine values of x.
x = linspace(0,10,150); y = cos(5*x);
Create a 2-D line plot of the cosine curve. Change the line color to a shade of blue-green using an RGB color value. Add a title and axis labels to the graph using the title, xlabel, and ylabel functions.
figure plot(x,y,'Color',[0,0.7,0.9]) title('2-D Line Plot') xlabel('x') ylabel('cos(5x)')
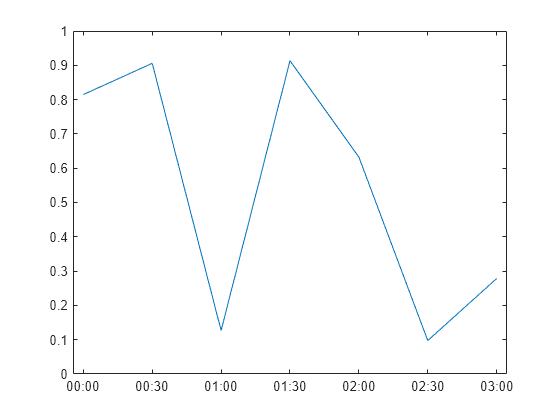
Define t as seven linearly spaced duration values between 0 and 3 minutes. Plot random data and specify the format of the duration tick marks using the 'DurationTickFormat' name-value pair argument.
t = 0:seconds(30):minutes(3); y = rand(1,7); plot(t,y,'DurationTickFormat','mm:ss')
Since R2022a
A convenient way to plot data from a table is to pass the table to the plot function and specify the variables to plot.
Read weather.csv as a timetable tbl. Then display the first three rows of the table.
tbl = readtimetable("weather.csv");
tbl = sortrows(tbl);
head(tbl,3) Time WindDirection WindSpeed Humidity Temperature RainInchesPerMinute CumulativeRainfall PressureHg PowerLevel LightIntensity
____________________ _____________ _________ ________ ___________ ___________________ __________________ __________ __________ ______________
25-Oct-2021 00:00:09 46 1 84 49.2 0 0 29.96 4.14 0
25-Oct-2021 00:01:09 45 1.6 84 49.2 0 0 29.96 4.139 0
25-Oct-2021 00:02:09 36 2.2 84 49.2 0 0 29.96 4.138 0
Plot the row times on the x-axis and the RainInchesPerMinute variable on the y-axis. When you plot data from a timetable, the row times are plotted on the x-axis by default. Thus, you do not need to specify the Time variable. Return the Line object as p. Notice that the axis labels match the variable names.
p = plot(tbl,"RainInchesPerMinute");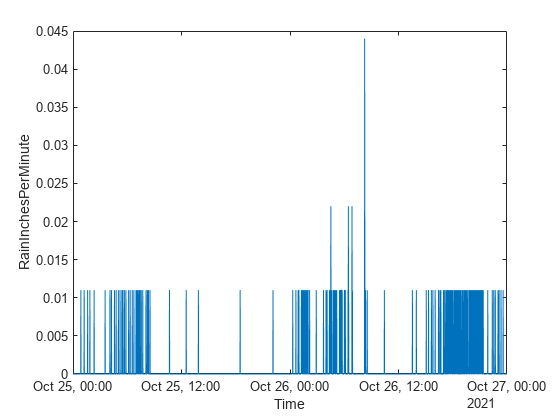
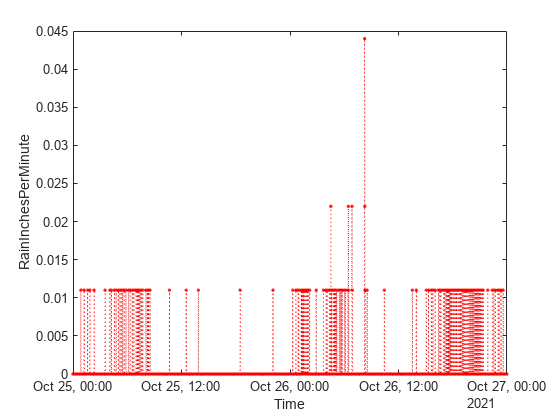
To modify aspects of the line, set the LineStyle, Color, and Marker properties on the Line object. For example, change the line to a red dotted line with point markers.
p.LineStyle = ":"; p.Color = "red"; p.Marker = ".";
Since R2022a
Read weather.csv as a timetable tbl, and display the first few rows of the table.
tbl = readtimetable("weather.csv");
head(tbl,3) Time WindDirection WindSpeed Humidity Temperature RainInchesPerMinute CumulativeRainfall PressureHg PowerLevel LightIntensity
____________________ _____________ _________ ________ ___________ ___________________ __________________ __________ __________ ______________
25-Oct-2021 00:00:09 46 1 84 49.2 0 0 29.96 4.14 0
25-Oct-2021 00:01:09 45 1.6 84 49.2 0 0 29.96 4.139 0
25-Oct-2021 00:02:09 36 2.2 84 49.2 0 0 29.96 4.138 0
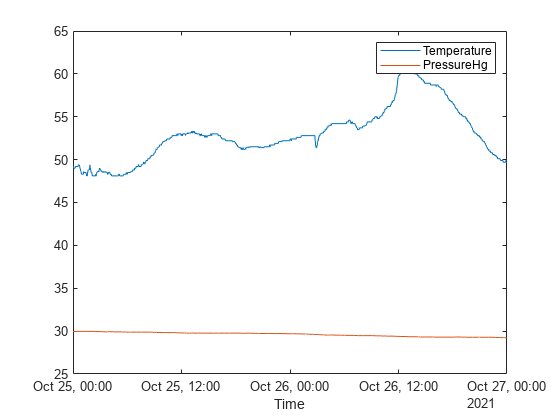
Plot the row times on the x-axis and the Temperature and PressureHg variables on the y-axis. When you plot data from a timetable, the row times are plotted on the x-axis by default. Thus, you do not need to specify the Time variable.
Add a legend. Notice that the legend labels match the variable names.
plot(tbl,["Temperature" "PressureHg"]) legend
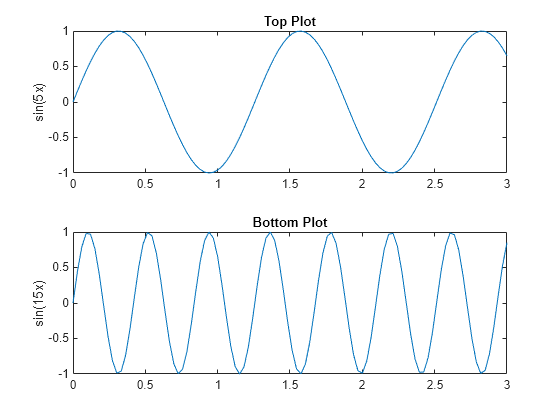
Call the tiledlayout function to create a 2-by-1 tiled chart layout. Call the nexttile function to create an axes object and return the object as ax1. Create the top plot by passing ax1 to the plot function. Add a title and y-axis label to the plot by passing the axes to the title and ylabel functions. Repeat the process to create the bottom plot.
% Create data and 2-by-1 tiled chart layout x = linspace(0,3); y1 = sin(5*x); y2 = sin(15*x); tiledlayout(2,1) % Top plot ax1 = nexttile; plot(ax1,x,y1) title(ax1,'Top Plot') ylabel(ax1,'sin(5x)') % Bottom plot ax2 = nexttile; plot(ax2,x,y2) title(ax2,'Bottom Plot') ylabel(ax2,'sin(15x)')
Define x as 100 linearly spaced values between and . Define y1 and y2 as sine and cosine values of x. Create a line plot of both sets of data and return the two chart lines in p.
x = linspace(-2*pi,2*pi); y1 = sin(x); y2 = cos(x); p = plot(x,y1,x,y2);
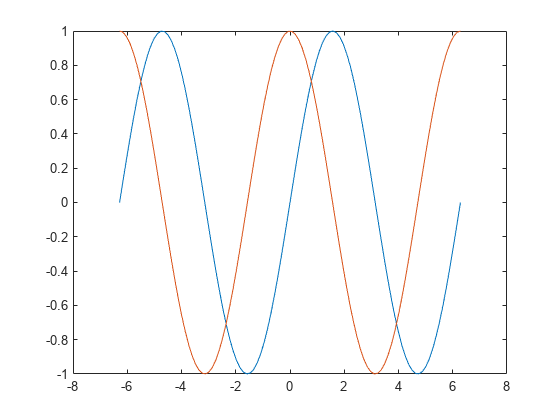
Change the line width of the first line to 2. Add star markers to the second line. Use dot notation to set properties.
p(1).LineWidth = 2;
p(2).Marker = '*';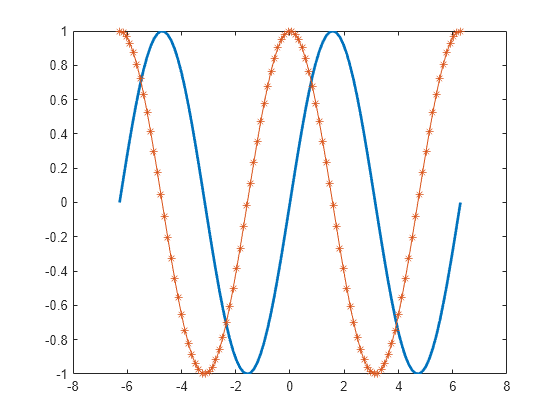
Plot a circle centered at the point (4,3) with a radius equal to 2. Use axis equal to use equal data units along each coordinate direction.
r = 2;
xc = 4;
yc = 3;
theta = linspace(0,2*pi);
x = r*cos(theta) + xc;
y = r*sin(theta) + yc;
plot(x,y)
axis equal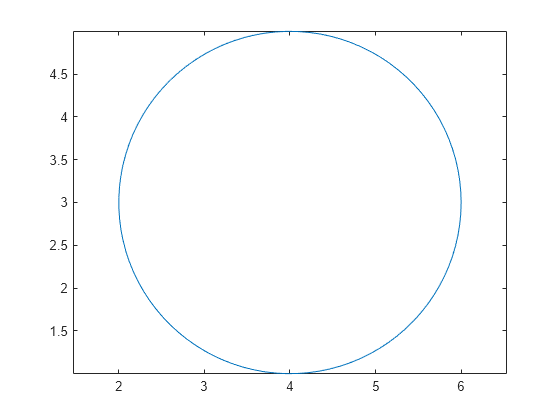
Input Arguments
x-coordinates, specified as a scalar, vector, or
matrix. The size and shape of X depends on the shape of
your data and the type of plot you want to create. This table describes the
most common situations.
| Type of Plot | How to Specify Coordinates |
|---|---|
| Single point | Specify plot(1,2,"o") |
| One set of points | Specify plot([1 2 3],[4; 5; 6]) |
| Multiple sets of points (using vectors) | Specify consecutive pairs of
plot([1 2 3],[4 5 6],[1 2 3],[7 8 9]) |
| Multiple sets of points (using matrices) | If all the sets share the same x- or y-coordinates, specify the shared coordinates as a vector and the other coordinates as a matrix. The length of the vector must match one of the dimensions of the matrix. For example: plot([1 2 3],[4 5 6; 7 8 9]) Alternatively, specify
plot([1 2 3; 4 5 6],[7 8 9; 10 11 12]) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
y-coordinates, specified as a scalar, vector, or
matrix. The size and shape of Y depends on the shape of
your data and the type of plot you want to create. This table describes the
most common situations.
| Type of Plot | How to Specify Coordinates |
|---|---|
| Single point | Specify plot(1,2,"o") |
| One set of points | Specify plot([1 2 3],[4; 5; 6]) Alternatively, specify just the y-coordinates. For example: plot([4 5 6]) |
| Multiple sets of points (using vectors) | Specify consecutive pairs of
plot([1 2 3],[4 5 6],[1 2 3],[7 8 9]) |
| Multiple sets of points (using matrices) | If all the sets share the same x- or y-coordinates, specify the shared coordinates as a vector and the other coordinates as a matrix. The length of the vector must match one of the dimensions of the matrix. For example: plot([1 2 3],[4 5 6; 7 8 9]) Alternatively, specify
plot([1 2 3; 4 5 6],[7 8 9; 10 11 12]) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
Line style, marker, and color, specified as a string scalar or character vector containing symbols. The symbols can appear in any order. You do not need to specify all three characteristics (line style, marker, and color). For example, if you omit the line style and specify the marker, then the plot shows only the marker and no line.
Example: "--or" is a red dashed line with circle markers.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
| Marker | Description | Resulting Marker |
|---|---|---|
"o" | Circle |
|
"+" | Plus sign |
|
"*" | Asterisk |
|
"." | Point |
|
"x" | Cross |
|
"_" | Horizontal line |
|
"|" | Vertical line |
|
"square" | Square |
|
"diamond" | Diamond |
|
"^" | Upward-pointing triangle |
|
"v" | Downward-pointing triangle |
|
">" | Right-pointing triangle |
|
"<" | Left-pointing triangle |
|
"pentagram" | Pentagram |
|
"hexagram" | Hexagram |
|
| Color Name | Short Name | RGB Triplet | Appearance |
|---|---|---|---|
"red" | "r" | [1 0 0] |
|
"green" | "g" | [0 1 0] |
|
"blue" | "b" | [0 0 1] |
|
"cyan"
| "c" | [0 1 1] |
|
"magenta" | "m" | [1 0 1] |
|
"yellow" | "y" | [1 1 0] |
|
"black" | "k" | [0 0 0] |
|
"white" | "w" | [1 1 1] |
|
Source table containing the data to plot, specified as a table or a timetable.
Table variables containing the x-coordinates, specified using one of the indexing schemes from the table.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
The table variables you specify can contain numeric, categorical,
datetime, or duration values. If xvar and
yvar both specify multiple variables, the number of
variables must be the same.
Example: plot(tbl,["x1","x2"],"y") specifies the table
variables named x1 and x2 for the
x-coordinates.
Example: plot(tbl,2,"y") specifies the second variable
for the x-coordinates.
Example: plot(tbl,vartype("numeric"),"y") specifies all
numeric variables for the x-coordinates.
Table variables containing the y-coordinates, specified using one of the indexing schemes from the table.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
The table variables you specify can contain numeric, categorical,
datetime, or duration values. If xvar and
yvar both specify multiple variables, the number of
variables must be the same.
Example: plot(tbl,"x",["y1","y2"]) specifies the table
variables named y1 and y2 for the
y-coordinates.
Example: plot(tbl,"x",2) specifies the second variable
for the y-coordinates.
Example: plot(tbl,"x",vartype("numeric")) specifies all
numeric variables for the y-coordinates.
Target axes, specified as an Axes object, a
PolarAxes object, or a
GeographicAxes object. If you do not specify the
axes, MATLAB plots into the current axes or it creates an
Axes object if one does not exist.
To create a polar plot or geographic plot, specify ax
as a PolarAxes or GeographicAxes
object. Alternatively, call the polarplot or geoplot function.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: plot([0 1],[2 3],LineWidth=2)
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: plot([0 1],[2 3],"LineWidth",2)
Note
The properties listed here are only a subset. For a complete list, see Line Properties.
Line color, specified as an RGB triplet, a hexadecimal color code, a color name, or a short name.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: "blue"
Example: [0
0 1]
Example: "#0000FF"
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the line has markers, then the line width also affects the marker edges.
The line width cannot be thinner than the width of a pixel. If you set the line width to a value that is less than the width of a pixel on your system, the line displays as one pixel wide.
Marker symbol, specified as one of the values listed in this table. By default, the object does not display markers. Specifying a marker symbol adds markers at each data point or vertex.
| Marker | Description | Resulting Marker |
|---|---|---|
"o" | Circle |
|
"+" | Plus sign |
|
"*" | Asterisk |
|
"." | Point |
|
"x" | Cross |
|
"_" | Horizontal line |
|
"|" | Vertical line |
|
"square" | Square |
|
"diamond" | Diamond |
|
"^" | Upward-pointing triangle |
|
"v" | Downward-pointing triangle |
|
">" | Right-pointing triangle |
|
"<" | Left-pointing triangle |
|
"pentagram" | Pentagram |
|
"hexagram" | Hexagram |
|
"none" | No markers | Not applicable |
Indices of data points at which to display markers, specified as a vector of positive integers. If you do not specify the indices, then MATLAB displays a marker at every data point.
Note
To see the markers, you must also specify a marker symbol.
Example: plot(x,y,"-o","MarkerIndices",[1 5 10]) displays a circle marker at
the first, fifth, and tenth data points.
Example: plot(x,y,"-x","MarkerIndices",1:3:length(y)) displays a cross
marker every three data points.
Example: plot(x,y,"Marker","square","MarkerIndices",5) displays one square
marker at the fifth data point.
Marker outline color, specified as "auto", an RGB triplet, a
hexadecimal color code, a color name, or a short name. The default value of
"auto" uses the same color as the Color
property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Marker fill color, specified as "auto", an RGB triplet, a hexadecimal
color code, a color name, or a short name. The "auto" option uses the
same color as the Color property of the parent axes. If you specify
"auto" and the axes plot box is invisible, the marker fill color is
the color of the figure.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Marker size, specified as a positive value in points, where 1 point = 1/72 of an inch.
Format for datetime tick labels, specified as the comma-separated pair
consisting of "DatetimeTickFormat" and a character
vector or string containing a date format. Use the letters
A-Z and a-z to construct a
custom format. These letters correspond to the Unicode® Locale Data Markup Language (LDML) standard for dates. You
can include non-ASCII letter characters such as a hyphen, space, or
colon to separate the fields.
If you do not specify a value for "DatetimeTickFormat", then
plot automatically optimizes and updates the
tick labels based on the axis limits.
Example: "DatetimeTickFormat","eeee, MMMM d, yyyy HH:mm:ss" displays a date
and time such as Saturday, April 19, 2014
21:41:06.
The following table shows several common display formats and examples of the formatted output for the date, Saturday, April 19, 2014 at 9:41:06 PM in New York City.
Value of DatetimeTickFormat | Example |
|---|---|
"yyyy-MM-dd" | 2014-04-19 |
"dd/MM/yyyy" | 19/04/2014 |
"dd.MM.yyyy" | 19.04.2014 |
"yyyy年 MM月
dd日" | 2014年 04月 19日 |
"MMMM d, yyyy" | April 19, 2014 |
"eeee, MMMM d, yyyy HH:mm:ss" | Saturday, April 19, 2014 21:41:06 |
"MMMM d, yyyy HH:mm:ss Z" | April 19, 2014 21:41:06 -0400 |
For a complete list of valid letter identifiers, see the Format property
for datetime arrays.
DatetimeTickFormat is not a chart line property.
You must set the tick format using the name-value pair argument when
creating a plot. Alternatively, set the format using the xtickformat and ytickformat functions.
The TickLabelFormat property of the datetime
ruler stores the format.
Format for duration tick labels, specified as the comma-separated pair
consisting of "DurationTickFormat" and a character
vector or string containing a duration format.
If you do not specify a value for "DurationTickFormat", then
plot automatically optimizes and updates the
tick labels based on the axis limits.
To display a duration as a single number that includes a fractional part, for example, 1.234 hours, specify one of the values in this table.
Value of DurationTickFormat | Description |
|---|---|
"y" | Number of exact fixed-length years. A fixed-length year is equal to 365.2425 days. |
"d" | Number of exact fixed-length days. A fixed-length day is equal to 24 hours. |
"h" | Number of hours |
"m" | Number of minutes |
"s" | Number of seconds |
Example: "DurationTickFormat","d" displays duration values in terms of
fixed-length days.
To display a duration in the form of a digital timer, specify one of these values.
"dd:hh:mm:ss""hh:mm:ss""mm:ss""hh:mm"
In addition, you can display up to nine fractional
second digits by appending up to nine S characters.
Example: "DurationTickFormat","hh:mm:ss.SSS" displays the milliseconds of a
duration value to three digits.
DurationTickFormat is not a chart line property.
You must set the tick format using the name-value pair argument when
creating a plot. Alternatively, set the format using the xtickformat and ytickformat functions.
The TickLabelFormat property of the duration
ruler stores the format.
Tips
Use
NaNandInfvalues to create breaks in the lines. For example, this code plots the first two elements, skips the third element, and draws another line using the last two elements:plot([1,2,NaN,4,5])
plotuses colors and line styles based on theColorOrderandLineStyleOrderproperties of the axes.plotcycles through the colors with the first line style. Then, it cycles through the colors again with each additional line style.You can change the colors and the line styles after plotting by setting the
ColorOrderorLineStyleOrderproperties on the axes. You can also call thecolororderfunction to change the color order for all the axes in the figure.
Extended Capabilities
The
plot function supports tall arrays with the following usage
notes and limitations:
Supported syntaxes for tall arrays
XandYare:plot(X,Y)plot(Y)plot(___,LineSpec)plot(___,Name,Value)plot(ax,___)
Xmust be in monotonically increasing order.Categorical inputs are not supported.
Tall inputs must be real column vectors.
With tall arrays, the
plotfunction plots in iterations, progressively adding to the plot as more data is read. During the updates, a progress indicator shows the proportion of data that has been plotted. Zooming and panning is supported during the updating process, before the plot is complete. To stop the update process, press the pause button in the progress indicator.
For more information, see Visualization of Tall Arrays.
The plot function
supports GPU array input with these usage notes and limitations:
This function accepts GPU arrays, but does not run on a GPU.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Usage notes and limitations:
This function operates on distributed arrays, but executes in the client MATLAB.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006aWhen you pass a table and one or more variable names to the plot function, the axis and legend labels now display any special characters that are included in the table variable names, such as underscores. Previously, special characters were interpreted as TeX or LaTeX characters.
For example, if you pass a table containing a variable named Sample_Number
to the plot function, the underscore appears in the axis and
legend labels. In R2022a and earlier releases, the underscores are interpreted as
subscripts.
| Release | Label for Table Variable "Sample_Number" |
|---|---|
R2022b |
|
R2022a |
|
To display axis and legend labels with TeX or LaTeX formatting, specify the labels manually.
For example, after plotting, call the xlabel or
legend function with the desired label strings.
xlabel("Sample_Number") legend(["Sample_Number" "Another_Legend_Label"])
Create plots by passing a table to the plot function followed by the variables you want to plot. When you specify your data as a table, the axis labels and the legend (if present) are automatically labeled using the table variable names.
See Also
Functions
Properties
External Websites
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)