spdiags
Extract nonzero diagonals and create sparse band and diagonal matrices
Syntax
Description
Examples
Create a tridiagonal matrix, change some of the matrix diagonals, and then extract the diagonals.
Create a 9-by-9 tridiagonal matrix by using a 1-by-3 vector of diagonal elements. View the matrix elements.
n = 9; A = spdiags([1 -2 1],-1:1,n,n); full(A)
ans = 9×9
-2 1 0 0 0 0 0 0 0
1 -2 1 0 0 0 0 0 0
0 1 -2 1 0 0 0 0 0
0 0 1 -2 1 0 0 0 0
0 0 0 1 -2 1 0 0 0
0 0 0 0 1 -2 1 0 0
0 0 0 0 0 1 -2 1 0
0 0 0 0 0 0 1 -2 1
0 0 0 0 0 0 0 1 -2
Change the values on the main (d = 0) diagonal of A.
Bin = abs(-(n-1)/2:(n-1)/2)'; d = 0; A = spdiags(Bin,d,A); full(A)
ans = 9×9
4 1 0 0 0 0 0 0 0
1 3 1 0 0 0 0 0 0
0 1 2 1 0 0 0 0 0
0 0 1 1 1 0 0 0 0
0 0 0 1 0 1 0 0 0
0 0 0 0 1 1 1 0 0
0 0 0 0 0 1 2 1 0
0 0 0 0 0 0 1 3 1
0 0 0 0 0 0 0 1 4
Finally, recover the diagonals of A as the columns in a matrix.
Bout = spdiags(A)
Bout = 9×3
1 4 0
1 3 1
1 2 1
1 1 1
1 0 1
1 1 1
1 2 1
1 3 1
0 4 1
Extract the nonzero diagonals of a matrix and examine the output format of spdiags.
Create a matrix containing a mix of nonzero and zero diagonals.
A = [0 5 0 10 0 0
0 0 6 0 11 0
3 0 0 7 0 12
1 4 0 0 8 0
0 2 5 0 0 9];Extract the nonzero diagonals from the matrix. Specify two outputs to return the diagonal numbers.
[Bout,d] = spdiags(A)
Bout = 5×4
0 0 5 10
0 0 6 11
0 3 7 12
1 4 8 0
2 5 9 0
d = 4×1
-3
-2
1
3
The columns of the first output Bout contain the nonzero diagonals of A. The second output d lists the indices of the nonzero diagonals of A. The longest nonzero diagonal in A is in column 3 of Bout. To give all columns of Bout the same length, the other nonzero diagonals of A have extra zeros added to their corresponding columns in Bout. For m-by-n matrices with m < n, the rules are:
For nonzero diagonals below the main diagonal of
A, extra zeros are added at the tops of columns (as in the first two columns ofBout).For nonzero diagonals above the main diagonal of
A, extra zeros are added at the bottoms of columns (as in the last column ofBout).
spdiags pads Bout with zeros in this manner even if the longest diagonal is not returned in Bout.
Create a 5-by-5 random matrix.
A = randi(10,5,5)
A = 5×5
9 1 2 2 7
10 3 10 5 1
2 6 10 10 9
10 10 5 8 10
7 10 9 10 7
Extract the main diagonal, and the first diagonals above and below it.
d = [-1 0 1]; Bout = spdiags(A,d)
Bout = 5×3
10 9 0
6 3 1
5 10 10
10 8 10
0 7 10
Try to extract the fifth super-diagonal (d = 5). Because A has only four super-diagonals, spdiags returns the diagonal as all zeros of the same length as the main (d = 0) diagonal.
B5 = spdiags(A,5)
B5 = 5×1
0
0
0
0
0
Examine how spdiags creates diagonals when the columns of the input matrix are longer than the diagonals they are replacing.
Create a 6-by-7 matrix of the numbers 1 through 6.
Bin = repmat((1:6)',[1 7])
Bin = 6×7
1 1 1 1 1 1 1
2 2 2 2 2 2 2
3 3 3 3 3 3 3
4 4 4 4 4 4 4
5 5 5 5 5 5 5
6 6 6 6 6 6 6
Use spdiags to create a square 6-by-6 matrix with several of the columns of Bin as diagonals. Because some of the diagonals only have one or two elements, there is a mismatch in sizes between the columns in Bin and diagonals in A.
d = [-4 -2 -1 0 3 4 5]; A = spdiags(Bin,d,6,6); full(A)
ans = 6×6
1 0 0 4 5 6
1 2 0 0 5 6
1 2 3 0 0 6
0 2 3 4 0 0
1 0 3 4 5 0
0 2 0 4 5 6
Each of the columns in Bin has six elements, but only the main diagonal in A has six elements. Therefore, all the other diagonals in A truncate the elements in the columns of Bin so that they fit on the selected diagonals:
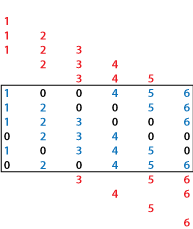
The way spdiags truncates the diagonals depends on the size of m-by-n matrix A. When , the behavior is as pictured above:
Diagonals below the main diagonal take elements from the tops of the columns first.
Diagonals above the main diagonal take elements from the bottoms of columns first.
This behavior reverses when :
A = spdiags(Bin,d,5,6); full(A)
ans = 5×6
1 0 0 1 1 1
2 2 0 0 2 2
3 3 3 0 0 3
0 4 4 4 0 0
5 0 5 5 5 0

Diagonals above the main diagonal take elements from the tops of the columns first.
Diagonals below the main diagonal take elements from the bottoms of columns first.
Input Arguments
Input matrix. This matrix is typically (but not necessarily) sparse.
Data Types: single | double | logical
Complex Number Support: Yes
Diagonal numbers, specified as a scalar or vector of integers. The diagonal numbers
follow the same conventions as diag:
d < 0is below the main diagonal, and satisfiesd >= -(m-1).d = 0is the main diagonal.d > 0is above the main diagonal, and satisfiesd <= (n-1).
An m-by-n matrix A has
(m + n - 1) diagonals. These diagonals are specified in the vector
d using indices from -(m-1) to
(n-1). For example, if A is 5-by-6, it has 10
diagonals, which are specified in the vector d using the indices –4,
–3, …, 4, 5. The following diagram illustrates this diagonal numbering.
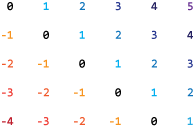
If you specify a diagonal that lies outside of A (such as
d = 7 in the example above), then spdiags
returns that diagonal as all zeros.
Example: spdiags(A,[3 5]) extracts the third and fifth diagonals
from A.
Diagonal elements, specified as a scalar, vector, or matrix. This argument is
typically (but not necessarily) full. spdiags uses the columns of
Bin to replace specified diagonals in A. If
the requested size of the output is m-by-n and
Bin is a column vector or matrix, then Bin
must have at least min(m,n) rows.
With the syntax S = spdiags(Bin,d,m,n), if a column of
Bin has more elements than the diagonal it is replacing, and
m >= n, then spdiags takes elements of
super-diagonals from the lower part of the column of
Bin, and elements of sub-diagonals from the
upper part of the column of Bin. However, if
m < n, then super-diagonals are from the
upper part of the column of Bin, and
sub-diagonals are from the lower part. For an example of this
behavior, see Columns and Diagonals of Different Sizes.
Data Types: single | double | logical
Complex Number Support: Yes
Dimension sizes, specified as nonnegative scalar integers.
spdiags uses these inputs to determine how large a matrix to
create.
Example: spdiags(Bin,d,300,400) creates a 300-by-400 matrix with
the columns of B placed along the specified diagonals
d.
Output Arguments
Diagonal elements, returned as a full matrix. The columns of Bout
contain diagonals extracted from A. Any elements of
Bout corresponding to positions outside of A are
set to zero.
Diagonal numbers, returned as a column vector. See d for a
description of the diagonal numbering.
Output matrix. S takes one of two forms:
With
S = spdiags(Bin,d,A), the specified diagonals inAare replaced with the columns inBinto create sparse matrixS.With
S = spdiags(Bin,d,m,n), them-by-nsparse matrixSis formed by taking the columns ofBinand placing them along the diagonals specified byd.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The spdiags function
supports GPU array input with these usage notes and limitations:
The first input cannot be sparse.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006aThe output of the three-input syntax and the four-input syntax of the
spdiags function is more consistent with the inputs, as shown in this
table.
| Syntax | Output Type in R2024b and Earlier | Output Type Starting in R2025a |
|---|---|---|
S = spdiags(Bin,d,A) |
| Same as A |
S = spdiags(Bin,d,m,n) |
| Same as Bin |
spdiags supports implicit expansion of the input argument
Bin. You can specify the diagonal elements as a scalar, vector, or
matrix, and the function expands the values if you specify a scalar or vector.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)