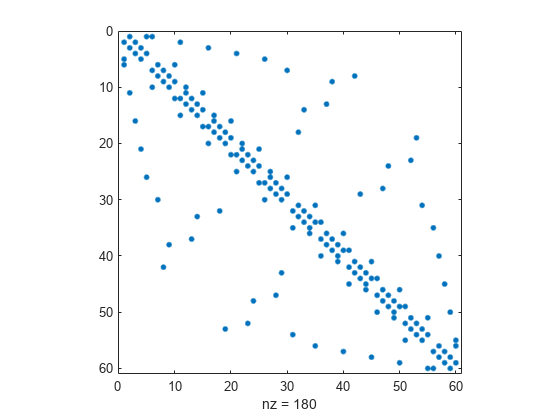
sprandn
Sparse normally distributed random matrix
Description
Examples
Input Arguments
Output Arguments
Limitations
sprandnis designed to produce large matrices with small density and will generate significantly fewer nonzero values than requested ifm*nis small ordensityis large.