Parking Valet Using Multistage Nonlinear Model Predictive Control
This example shows how to use the Vehicle Path Planner System block in Simulink® for a parking valet using multistage nonlinear model predictive control (NLMPC).
Parking Garage
In this example, the parking garage contains an ego vehicle and eight static obstacles. The obstacles are given by six parked vehicles, a reserved parking area, and the garage border. The goal of the ego vehicle is to park at a target pose without colliding with any of the obstacles. The reference point of the ego pose is located at the center of the rear axle.
Specify the initial ego vehicle pose.
% Ego initial pose: x(m), y(m) and yaw angle (rad)
egoInitialPose = [4,12,0];Define the target pose for the ego vehicle.
% Ego target pose: x(m), y(m) and yaw angle (rad)
egoTargetPose = [27.2,4.7,-pi/2];The helperSLCreateCostmap function creates a static map of the parking lot that contains information about stationary obstacles, road markings, and parked cars. For more details, see the Automated Parking Valet in Simulink (Automated Driving Toolbox) example.
costmap = helperSLCreateCostmap(); helperSLCreateUtilityBus; costmapStruct = helperSLCreateUtilityStruct(costmap);
Visualize the parking environment. Use a sample time of 0.1 for the visualizer.
Tv = 0.1; helperSLVisualizeParkingValet(egoInitialPose,0,costmapStruct);
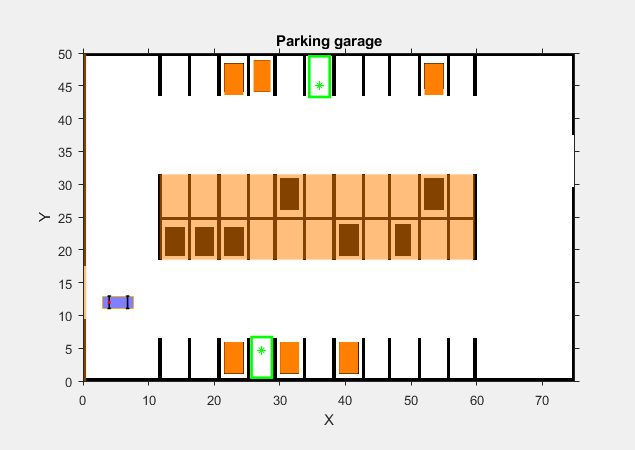
The six parked vehicles are orange boxes on the top and bottom of the figure. The middle area represents the reserved parking area. The left border of the garage is also modeled as a static obstacle. The ego vehicle in blue has two axles and four wheels. The two green boxes represent the target parking spots for the ego vehicle, with the top spot facing north.
Configuration of Vehicle Path Planner System Block
Define the parameters of the ego vehicle.
vdims = vehicleDimensions; egoWheelbase = vdims.Wheelbase; distToCenter = 0.5*egoWheelbase;
Define the parameters of the eight obstacles. Each row of obsMat represents an obstacle with five elements: position (x,y), heading angle, length, and width
numObs = 8; obsMat = [23,3.55,0,2.9,4.8;... 31.5,3.55,0,2.9,4.8;... 40.5,3.55,0,2.9,4.8;... 23,46,0,2.9,4.8;... 27.3,46.5,0,2.6,4.8;... 53.5,46,0,2.9,4.8;... 0.25,25,0,0.5,50;... 35.7,25,0,48,13];
Define the sample time and prediction horizon for the MPC controller.
TsPlanner = 1; pPlanner = 20;
The velocity of the ego vehicle is constrained to the range [-6.5,6.5] m/s (approximately 15 mph) and the steering angle of the ego vehicle is constrained to the range [-45,45] degrees.
v_range = [-6.5,6.5]; steer_range = [-pi/4,pi/4];
Define the safe distance in meters. To avoid collision with obstacles, the minimum distance to all obstacles must be greater than a safe distance.
d_safe = 0.1;
Together with the pose of ego car and the target pose, the Vehicle Path Planner System block can generate a reference path from the current pose of the ego car to a target pose.
Track Reference Trajectory in Simulink Model
Design an NLMPC controller to track the reference trajectory.
First, set the simulation duration.
Duration = 15; Ts = 0.1; Tsteps = Duration/Ts;
Then, specify the start and end times for planning.
tmin = 5; % start time for planning tmax = tmin + 0.5; % end time for planning
Create an NLMPC controller with a tracking prediction horizon (pTracking) of 10.
pTracking = 10; nlobjTracking = createMPCForTrackingVPP(pTracking);
Open the Simulink model.
mdl = 'parkingValetVPP';
open_system(mdl)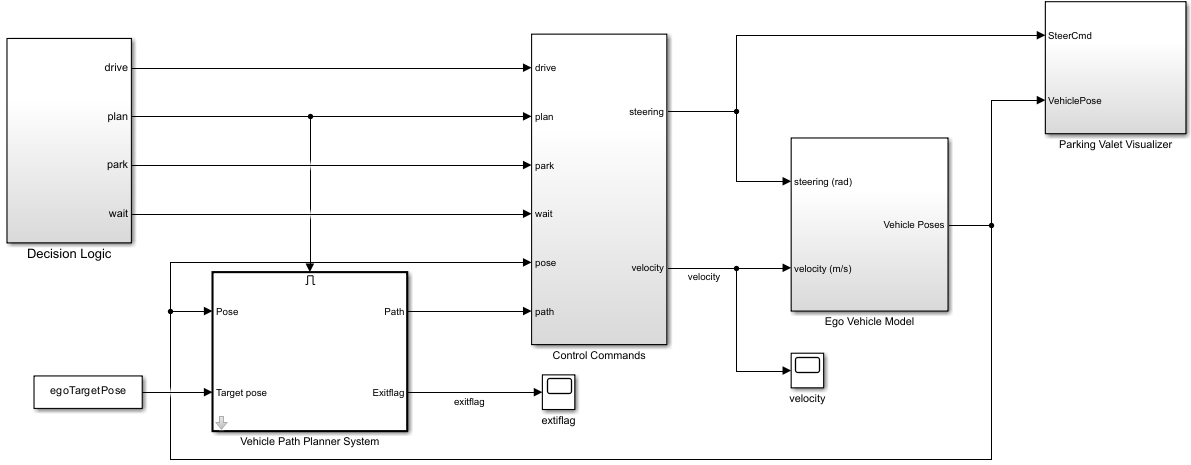
Run the simulation. During the simulation, the Vehicle Path Planner System block plans the path to the target pose. Then, the NLMPC tracking controller follows the planned path into the parking spot.
sim(mdl);
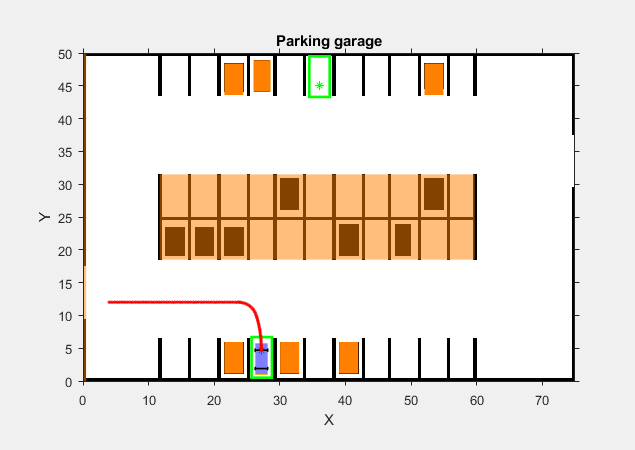
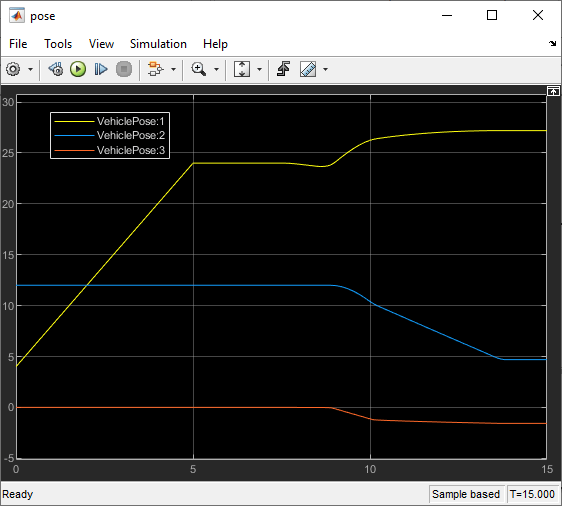
The animation shows that the ego vehicle parks at the target pose successfully without any obstacle collisions. You can also view the ego vehicle pose trajectories using the scopes.
open_system(mdl + "/Parking Valet Visualizer/pose")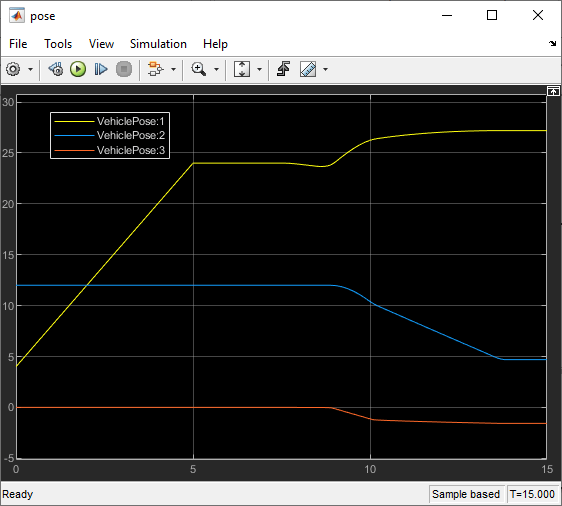
Uncomment the following lines to run the model from another start pose to target pose.
% egoInitialPose = [4,35,0]; % egoTargetPose = [36,45,pi/2]; % sim(mdl)
Conclusion
This example shows how to generate a reference trajectory and track the trajectory for parking valet using nonlinear model predictive control. The controller navigates the ego vehicle to the target parking spot without colliding with any obstacles.
mpcverbosity('on'); bdclose(mdl) f = findobj('Name','Automated Parking Valet'); close(f)