Office Assignments by Binary Integer Programming: Problem-Based
This example shows how to solve an assignment problem by binary integer programming using the optimization problem approach. For the solver-based approach, see Office Assignments by Binary Integer Programming: Solver-Based.
Office Assignment Problem
You want to assign six people, Marcelo, Rakesh, Peter, Tom, Marjorie, and Mary Ann, to seven offices. Each office can have no more than one person, and each person gets exactly one office. So there will be one empty office. People can give preferences for the offices, and their preferences are considered based on their seniority. The longer they have been at MathWorks, the higher the seniority. Some offices have windows, some do not, and one window is smaller than others. Additionally, Peter and Tom often work together, so should be in adjacent offices. Marcelo and Rakesh often work together, and should be in adjacent offices.
Office Layout
Offices 1, 2, 3, and 4 are inside offices (no windows). Offices 5, 6, and 7 have windows, but the window in office 5 is smaller than the other two. Here is how the offices are arranged.
officelist = {'Office 1','Office 2','Office 3','Office 4','Office 5','Office 6','Office 7'};
printofficeassign(officelist)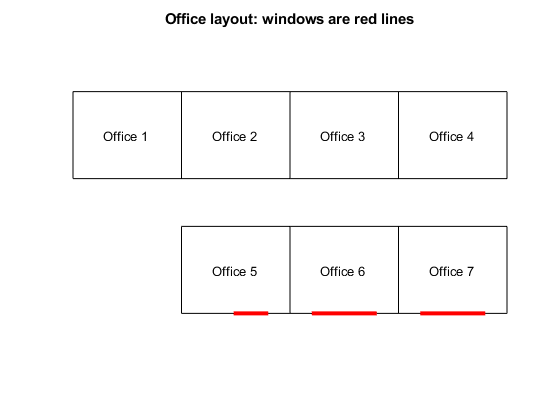
Problem Formulation
You need to formulate the problem mathematically. Create binary variables that indicate whether a person occupies an office. The list of people's names is
namelist = {'Mary Ann','Marjorie','Tom','Peter','Marcelo','Rakesh'};Create binary variables indexed by office number and name.
occupy = optimvar('occupy',namelist,officelist,... 'Type','integer','LowerBound',0,'Upperbound',1);
Seniority
You want to weight the preferences based on seniority so that the longer you have been at MathWorks, the more your preferences count. The seniority is as follows: Mary Ann 9 years, Marjorie 10 years, Tom 5 years, Peter 3 years, Marcelo 1.5 years, and Rakesh 2 years. Create a normalized weight vector based on seniority.
seniority = [9 10 5 3 1.5 2]; weightvector = seniority/sum(seniority);
People's Office Preferences
Set up a preference matrix where the rows correspond to offices and the columns correspond to people. Ask each person to give values for each office so that the sum of all their choices, i.e., their column, sums to 100. A higher number means the person prefers the office. Each person's preferences are listed in a column vector.
MaryAnn = [0, 0, 0, 0, 10, 40, 50]; Marjorie = [0, 0, 0, 0, 20, 40, 40]; Tom = [0, 0, 0, 0, 30, 40, 30]; Peter = [1, 3, 3, 3, 10, 40, 40]; Marcelo = [3, 4, 1, 2, 10, 40, 40]; Rakesh = [10, 10, 10, 10, 20, 20, 20];
The ith element of a person's preference vector is how highly they value the ith office. Thus, the combined preference matrix is as follows.
prefmatrix = [MaryAnn;Marjorie;Tom;Peter;Marcelo;Rakesh];
Weight the preferences matrix by weightvector to scale the columns by seniority.
PM = diag(weightvector) * prefmatrix;
Objective Function
The objective is to maximize the satisfaction of the preferences weighted by seniority. This is the linear objective function sum(sum(occupy.*PM)).
Create an optimization problem and include the objective function.
peopleprob = optimproblem('ObjectiveSense','maximize','Objective',sum(sum(occupy.*PM)));
Constraints
The first set of constraints requires that each person gets exactly one office, that is for each person, the sum of the occupy values corresponding to that person is exactly one.
peopleprob.Constraints.constr1 = sum(occupy,2) == 1;
The second set of constraints are inequalities. These constraints specify that each office has no more than one person in it.
peopleprob.Constraints.constr2 = sum(occupy,1) <= 1;
You want Tom and Peter no more than one office away from each other, and the same with Marcelo and Rakesh.
Set constraints that Tom and Peter are not more than 1 away from each other.
peopleprob.Constraints.constrpt1 = occupy('Tom','Office 1') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') <= 1; peopleprob.Constraints.constrpt2 = occupy('Tom','Office 2') + sum(occupy('Peter',:)) - occupy('Peter','Office 1') ... - occupy('Peter','Office 3') - occupy('Peter','Office 5') <= 1; peopleprob.Constraints.constrpt3 = occupy('Tom','Office 3') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') ... - occupy('Peter','Office 4') - occupy('Peter','Office 6') <= 1; peopleprob.Constraints.constrpt4 = occupy('Tom','Office 4') + sum(occupy('Peter',:)) - occupy('Peter','Office 3') ... - occupy('Peter','Office 7') <= 1; peopleprob.Constraints.constrpt5 = occupy('Tom','Office 5') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') ... - occupy('Peter','Office 6') <= 1; peopleprob.Constraints.constrpt6 = occupy('Tom','Office 6') + sum(occupy('Peter',:)) - occupy('Peter','Office 3') ... - occupy('Peter','Office 5') - occupy('Peter','Office 7') <= 1; peopleprob.Constraints.constrpt7 = occupy('Tom','Office 7') + sum(occupy('Peter',:)) - occupy('Peter','Office 4') ... - occupy('Peter','Office 6') <= 1;
Now create constraints that Marcelo and Rakesh are not more than 1 away from each other.
peopleprob.Constraints.constmr1 = occupy('Marcelo','Office 1') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') <= 1; peopleprob.Constraints.constmr2 = occupy('Marcelo','Office 2') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 1') ... - occupy('Rakesh','Office 3') - occupy('Rakesh','Office 5') <= 1; peopleprob.Constraints.constmr3 = occupy('Marcelo','Office 3') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') ... - occupy('Rakesh','Office 4') - occupy('Rakesh','Office 6') <= 1; peopleprob.Constraints.constmr4 = occupy('Marcelo','Office 4') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 3') ... - occupy('Rakesh','Office 7') <= 1; peopleprob.Constraints.constmr5 = occupy('Marcelo','Office 5') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') ... - occupy('Rakesh','Office 6') <= 1; peopleprob.Constraints.constmr6 = occupy('Marcelo','Office 6') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 3') ... - occupy('Rakesh','Office 5') - occupy('Rakesh','Office 7') <= 1; peopleprob.Constraints.constmr7 = occupy('Marcelo','Office 7') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 4') ... - occupy('Rakesh','Office 6') <= 1;
Solve Assignment Problem
Call solve to solve the problem.
[soln,fval,exitflag,output] = solve(peopleprob);
LP: Optimal objective value is -33.836066. Optimal solution found. Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).
View the Solution -- Who Got Each Office?
numOffices = length(officelist); office = cell(numOffices,1); for i=1:numOffices office{i} = find(soln.occupy(:,i)); % people index in office end whoinoffice = officelist; % allocate for i=1:numOffices if isempty(office{i}) whoinoffice{i} = ' empty '; else whoinoffice{i} = namelist(office{i}); end end printofficeassign(whoinoffice); title('Solution of the Office Assignment Problem');
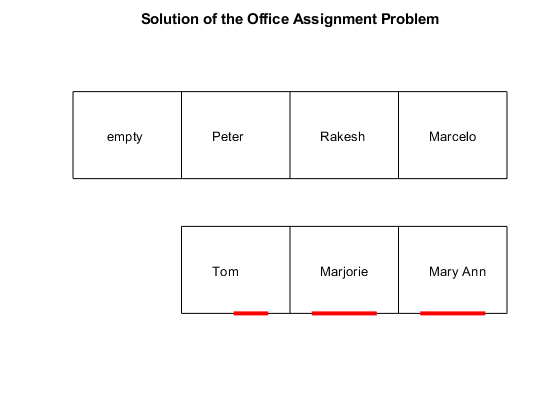
Solution Quality
For this problem, the satisfaction of the preferences by seniority is maximized to the value of fval. The value of exitflag indicates that solve converged to an optimal solution. The output structure gives information about the solution process, such as how many nodes were explored, and the gap between the lower and upper bounds in the branching calculation. In this case, no branch-and-bound nodes were generated, meaning the problem was solved without a branch-and-bound step. The absolute gap is 0, meaning the solution is optimal, with no difference between the internally calculated lower and upper bounds on the objective function.
fval,exitflag,output
fval = 33.8361
exitflag = 1
output = struct with fields:
relativegap: 0
absolutegap: 0
numfeaspoints: 1
numnodes: 0
constrviolation: 0
message: 'Optimal solution found.↵↵Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).'
solver: 'intlinprog'