Increasing Angular Resolution with Virtual Arrays
This example introduces how forming a virtual array in MIMO radars can help increase angular resolution. It shows how to simulate a coherent MIMO radar signal processing chain using Phased Array System Toolbox™.
Introduction
There are two categories of multiple input multiple output (MIMO) radars. Multistatic radars form the first category. They are often referred to as statistical MIMO radars. Coherent MIMO radars form the second category and are the focus of this example. A benefit of coherent MIMO radar signal processing is the ability to increase the angular resolution of the physical antenna array by forming a virtual array.
Virtual Array
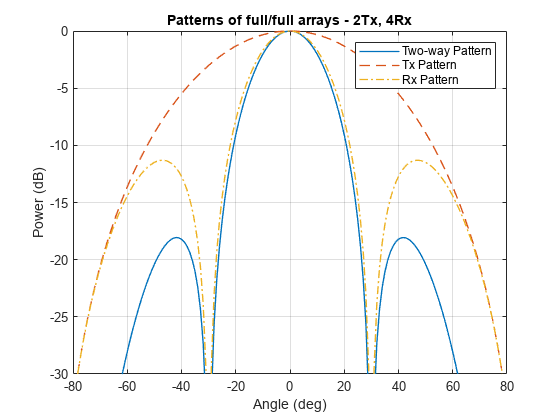
A virtual array can be created by quasi-monostatic MIMO radars, where the transmit and receive arrays are closely located. To better understand the virtual array concept, first look at the two-way pattern of a conventional phased array radar. The two-way pattern of a phased array radar is the product of its transmit array pattern and receive array pattern. For example, consider a 77 GHz millimeter wave radar with a 2-element transmit array and a 4-element receive array.
fc = 77e9; c = 3e8; lambda = c/fc; Nt = 2; Nr = 4;
If both arrays have half-wavelength spacing, which are sometimes referred to as full arrays, then the two-way pattern is close to the receive array pattern.
dt = lambda/2; dr = lambda/2; txarray = phased.ULA(Nt,dt); rxarray = phased.ULA(Nr,dr); ang = -90:90; pattx = pattern(txarray,fc,ang,0,'Type','powerdb'); patrx = pattern(rxarray,fc,ang,0,'Type','powerdb'); pat2way = pattx+patrx; helperPlotMultipledBPattern(ang,[pat2way pattx patrx],[-30 0],... {'Two-way Pattern','Tx Pattern','Rx Pattern'},... 'Patterns of full/full arrays - 2Tx, 4Rx',... {'-','--','-.'});
If the full transmit array is replaced with a thin array, meaning the element spacing is wider than half wavelength, then the two-way pattern has a narrower beamwidth. Notice that even though the thin transmit array has grating lobes, those grating lobes are not present in the two-way pattern.
dt = Nr*lambda/2; txarray = phased.ULA(Nt,dt); pattx = pattern(txarray,fc,ang,0,'Type','powerdb'); pat2way = pattx+patrx; helperPlotMultipledBPattern(ang,[pat2way pattx patrx],[-30 0],... {'Two-way Pattern','Tx Pattern','Rx Pattern'},... 'Patterns of thin/full arrays - 2Tx, 4Rx',... {'-','--','-.'});

The two-way pattern of this system corresponds to the pattern of a virtual receive array with 2 x 4 = 8 elements. Thus, by carefully choosing the geometry of the transmit and the receive arrays, we can increase the angular resolution of the system without adding more antennas to the arrays.

varray = phased.ULA(Nt*Nr,dr); patv = pattern(varray,fc,ang,0,'Type','powerdb'); helperPlotMultipledBPattern(ang,[pat2way patv],[-30 0],... {'Two-way Pattern','Virtual Array Pattern'},... 'Patterns of thin/full arrays and virtual array',... {'-','--'},[1 2]);

Virtual Array in MIMO Radars
In a coherent MIMO radar system, each antenna of the transmit array transmits an orthogonal waveform. Because of this orthogonality, it is possible to recover the transmitted signals at the receive array. The measurements at the physical receive array corresponding to each orthogonal waveform can then be stacked to form the measurements of the virtual array.

Note that since each element in the transmit array radiates independently, there is no transmit beamforming, so the transmit pattern is broad and covers a large field of view (FOV). This allows the simultaneous illumination of all targets in the FOV. The receive array can then generate multiple beams to process all target echoes. Compared to conventional phased array radars that need successive scans to cover the entire FOV, this is another advantage of MIMO radars for applications that require fast reaction time.
TDM-MIMO Radar Simulation
Time division multiplexing (TDM) is one way to achieve orthogonality among transmit channels. The remainder of this example shows how to model and simulate a TDM-MIMO frequency-modulated continuous wave (FMCW) automotive radar system. The waveform characteristics are adapted from the Automotive Adaptive Cruise Control Using FMCW Technology (Radar Toolbox) example.
waveform = helperDesignFMCWWaveform(c,lambda); fs = waveform.SampleRate;
Imagine that there are two cars in the FOV with a separation of 20 degrees. As seen in the earlier array pattern plots of this example, the 3dB beamwidth of a 4-element receive array is around 30 degrees so conventional processing would not be able to separate the two targets in the angular domain. The radar sensor parameters are as follows:
transmitter = phased.Transmitter('PeakPower',0.001,'Gain',36); receiver = phased.ReceiverPreamp('Gain',40,'NoiseFigure',4.5,'SampleRate',fs); txradiator = phased.Radiator('Sensor',txarray,'OperatingFrequency',fc,... 'PropagationSpeed',c,'WeightsInputPort',true); rxcollector = phased.Collector('Sensor',rxarray,'OperatingFrequency',fc,... 'PropagationSpeed',c);
Define the position and motion of the ego vehicle and the two cars in the FOV.
radar_speed = 100*1000/3600; % Ego vehicle speed 100 km/h radarmotion = phased.Platform('InitialPosition',[0;0;0.5],'Velocity',[radar_speed;0;0]); car_dist = [40 50]; % Distance between sensor and cars (meters) car_speed = [-80 96]*1000/3600; % km/h -> m/s car_az = [-10 10]; car_rcs = [20 40]; car_pos = [car_dist.*cosd(car_az);car_dist.*sind(car_az);0.5 0.5]; cars = phased.RadarTarget('MeanRCS',car_rcs,'PropagationSpeed',c,'OperatingFrequency',fc); carmotion = phased.Platform('InitialPosition',car_pos,'Velocity',[car_speed;0 0;0 0]);
The propagation model is assumed to be free space.
channel = phased.FreeSpace('PropagationSpeed',c,... 'OperatingFrequency',fc,'SampleRate',fs,'TwoWayPropagation',true);
The raw data cube received by the physical array of the TDM MIMO radar can then be simulated as follows:
rng(2017); Nsweep = 64; Dn = 2; % Decimation factor fs = fs/Dn; xr = complex(zeros(fs*waveform.SweepTime,Nr,Nsweep)); w0 = [0;1]; % weights to enable/disable radiating elements for m = 1:Nsweep % Update radar and target positions [radar_pos,radar_vel] = radarmotion(waveform.SweepTime); [tgt_pos,tgt_vel] = carmotion(waveform.SweepTime); [~,tgt_ang] = rangeangle(tgt_pos,radar_pos); % Transmit FMCW waveform sig = waveform(); txsig = transmitter(sig); % Toggle transmit element w0 = 1-w0; txsig = txradiator(txsig,tgt_ang,w0); % Propagate the signal and reflect off the target txsig = channel(txsig,radar_pos,tgt_pos,radar_vel,tgt_vel); txsig = cars(txsig); % Dechirp the received radar return rxsig = rxcollector(txsig,tgt_ang); rxsig = receiver(rxsig); dechirpsig = dechirp(rxsig,sig); % Decimate the return to reduce computation requirements for n = size(xr,2):-1:1 xr(:,n,m) = decimate(dechirpsig(:,n),Dn,'FIR'); end end
Virtual Array Processing for TDM-MIMO Radar
The data cube received by the physical array must be processed to form the virtual array data cube. For the TDM-MIMO radar system used in this example, the measurements corresponding to the two transmit antenna elements can be recovered from two consecutive sweeps by taking every other page of the data cube.
xr1 = xr(:,:,1:2:end); xr2 = xr(:,:,2:2:end);
Now the data cube in xr1 contains the return corresponding to the first transmit antenna element, and the data cube in xr2 contains the return corresponding to the second transmit antenna element. Hence, the data cube from the virtual array can be formed as:
xrv = cat(2,xr1,xr2);
Next, perform range-Doppler processing on the virtual data cube. Because the range-Doppler processing is linear, the phase information is preserved. Therefore, the resulting response can be used later to perform further spatial processing on the virtual aperture.
nfft_r = 2^nextpow2(size(xrv,1)); nfft_d = 2^nextpow2(size(xrv,3)); rngdop = phased.RangeDopplerResponse('PropagationSpeed',c,... 'DopplerOutput','Speed','OperatingFrequency',fc,'SampleRate',fs,... 'RangeMethod','FFT','PRFSource','Property',... 'RangeWindow','Hann','PRF',1/(Nt*waveform.SweepTime),... 'SweepSlope',waveform.SweepBandwidth/waveform.SweepTime,... 'RangeFFTLengthSource','Property','RangeFFTLength',nfft_r,... 'DopplerFFTLengthSource','Property','DopplerFFTLength',nfft_d,... 'DopplerWindow','Hann'); [resp,r,sp] = rngdop(xrv);
The resulting resp is a data cube containing the range-Doppler response for each element in the virtual array. As an illustration, the range-Doppler map for the first element in the virtual array is shown.
plotResponse(rngdop,squeeze(xrv(:,1,:)));

The detection can be performed on the range-Doppler map from each pair of transmit and receive element to identify the targets in scene. In this example, a simple threshold-based detection is performed on the map obtained between the first transmit element and the first receive element, which corresponds to the measurement at the first element in the virtual array. Based on the range-Doppler map shown in the previous figure, the threshold is set at 10 dB below the maximum peak.
respmap = squeeze(mag2db(abs(resp(:,1,:)))); ridx = helperRDDetection(respmap,-10);
Based on the detected range of the targets, the corresponding range cuts can be extracted from the virtual array data cube to perform further spatial processing. To verify that the virtual array provides a higher resolution compared to the physical array, the code below extracts the range cuts for both targets and combines them into a single data matrix. The beamscan algorithm is then performed over these virtual array measurements to estimate the directions of the targets.
xv = squeeze(sum(resp(ridx,:,:),1))'; doa = phased.BeamscanEstimator('SensorArray',varray,'PropagationSpeed',c,... 'OperatingFrequency',fc,'DOAOutputPort',true,'NumSignals',2,'ScanAngles',ang); [Pdoav,target_az_est] = doa(xv); fprintf('target_az_est = [%s]\n',num2str(target_az_est));
target_az_est = [-6 10]
The two targets are successfully separated. The actual angles for the two cars are -10 and 10 degrees.
The next figure compares the spatial spectrums from the virtual and the physical receive array.
doarx = phased.BeamscanEstimator('SensorArray',rxarray,'PropagationSpeed',c,... 'OperatingFrequency',fc,'DOAOutputPort',true,'ScanAngles',ang); Pdoarx = doarx(xr); helperPlotMultipledBPattern(ang,mag2db(abs([Pdoav Pdoarx])),[-30 0],... {'Virtual Array','Physical Array'},... 'Spatial spectrum for virtual array and physical array',{'-','--'});

In this example, the detection is performed on the range-Doppler map without spatial processing of the virtual array data cube. This works because the SNR is high. If the SNR is low, it is also possible to process the virtual array blindly across the entire range-Doppler map to maximize the SNR before the detection.
Phase-coded MIMO Radars
Although a TDM-MIMO radar's processing chain is relatively simple, it uses only one transmit antenna at a time. Therefore, it does not take advantage of the full capacity of the transmit array. To improve the efficiency, there are other orthogonal waveforms that can be used in a MIMO radar.
For instance, a MIMO radars can also adopt a phase-coded MIMO waveform. In this case, each radiating element can transmit a uniquely coded waveform, and the receiver can then have a matched filter bank corresponding to each of those phase coded waveform. The signals can then be recovered and processed to form the virtual array. Using the same system configuration as in previous sections, one phase-coded scheme to achieve orthogonality is to have one element always transmit the same FMCW waveform, while the second transmit element reverses the phase of the FMCW waveform for each sweep. This way both transmit elements are active in all sweeps. For the first sweep, the two elements transmit the same waveform; and for the second sweep, the two elements transmit the waveform with opposite phase, and so on. This is essentially coding the consecutive sweeps from different elements with a Hadamard code. It is similar to the Alamouti codes used in MIMO communication systems.
The raw data cube received by the physical array of the Phase-Coded MIMO radar can then be simulated as follows:
rng(2018); xr = complex(zeros(fs*waveform.SweepTime,Nr,Nsweep)); w = hadamard(2); % weights to enable/disable radiating elements for m = 1:Nsweep % Update radar and target positions [radar_pos,radar_vel] = radarmotion(waveform.SweepTime); [tgt_pos,tgt_vel] = carmotion(waveform.SweepTime); [~,tgt_ang] = rangeangle(tgt_pos,radar_pos); % Transmit FMCW waveform sig = waveform(); txsig = transmitter(sig); % Toggle transmit element if mod(m,2) == 1 w0 = w(:,1); else w0 = w(:,2); end txsig = txradiator(txsig,tgt_ang,w0); % Propagate the signal and reflect off the target txsig = channel(txsig,radar_pos,tgt_pos,radar_vel,tgt_vel); txsig = cars(txsig); % Dechirp the received radar return rxsig = rxcollector(txsig,tgt_ang); rxsig = receiver(rxsig); dechirpsig = dechirp(rxsig,sig); % Decimate the return to reduce computation requirements for n = size(xr,2):-1:1 xr(:,n,m) = decimate(dechirpsig(:,n),Dn,'FIR'); end end
Virtual Array Processing for Phase-coded MIMO Radar
For the Phase-Coded MIMO radar system used in this example, the measurements corresponding to the two sets of phase code can be recovered from two consecutive sweeps by taking every other page of the data cube.
Nvsweep = Nsweep/2; xr1 = xr(:,:,1:2:end); xr2 = xr(:,:,2:2:end);
Next, perform range-Doppler processing on the two data cubes separately.
nfft_r = 2^nextpow2(size(xr1,1)); nfft_d = 2^nextpow2(size(xr1,3)); rngdop = phased.RangeDopplerResponse('PropagationSpeed',c,... 'DopplerOutput','Speed','OperatingFrequency',fc,'SampleRate',fs,... 'RangeMethod','FFT','PRFSource','Property',... 'RangeWindow','Hann','PRF',1/(Nt*waveform.SweepTime),... 'SweepSlope',waveform.SweepBandwidth/waveform.SweepTime,... 'RangeFFTLengthSource','Property','RangeFFTLength',nfft_r,... 'DopplerFFTLengthSource','Property','DopplerFFTLength',nfft_d,... 'DopplerWindow','Hann');
As an illustration, the range-Doppler map of Phase-Coded MIMO radar is same as that of TDM MIMO radar.
plotResponse(rngdop,squeeze(xr1(:,1,:)));

For a phase-coded MIMO radar, the virtual array can no longer be formed by simply cascading the signal from the two adjacent pulses together. Instead, before cascading, the phase code embedded in pulses has to be corrected. This example uses a Hadamard code based approach, thus the process to remove the embedded phases is referred to as Hadamard decode process. After the Hadamard decode processing, range-Doppler responses of different transmitters are cascaded. The resulting respvr is a data cube containing the range-Doppler response for physical arrays from different transmit antenna elements.
resp_DDM(:,:,:,1) = rngdop(xr1); [resp_DDM(:,:,:,2),r,sp] = rngdop(xr2); respvr(:,:,:,1) = helperHadamardDecode(resp_DDM,w(:,1)); respvr(:,:,:,2) = helperHadamardDecode(resp_DDM,w(:,2)); % for i = 1:2 % H = w(:,i); % respvr(:,:,:,i) = hadamard_decode(resp_DDM,H); % end
Hence, the data cube from the virtual array can be formed as:
resp_vr = cat(2,respvr(:,:,:,1),respvr(:,:,:,2));
The detection can be performed on the range-Doppler map from each pair of transmit and receive element to identify the targets in scene. In this example, a simple threshold-based detection is performed on the map obtained between the first transmit element and the first receive element, which corresponds to the measurement at the first element in the virtual array. Based on the range-Doppler map shown in the previous figure, the threshold is set at 10 dB below the maximum peak.
respmap = squeeze(mag2db(abs(resp_vr(:,1,:)))); ridx = helperRDDetection(respmap,-10);
Based on the detected range of the targets, the corresponding range cuts can be extracted from the virtual array data cube to perform further spatial processing. To verify that the virtual array provides a higher resolution compared to the physical array, the code below extracts the range cuts for both targets and combines them into a single data matrix. The beamscan algorithm is then performed over these virtual array measurements to estimate the directions of the targets.
xv = squeeze(sum(resp_vr(ridx,:,:),1))'; doa = phased.BeamscanEstimator('SensorArray',varray,'PropagationSpeed',c,... 'OperatingFrequency',fc,'DOAOutputPort',true,'NumSignals',2,'ScanAngles',ang); [Pdoav,target_az_est] = doa(xv); fprintf('target_az_est = [%s]\n',num2str(target_az_est));
target_az_est = [10 -11]
The two targets are successfully separated. The actual angles for the two cars are -10 and 10 degrees.
The next figure compares the spatial spectrums from the virtual and the physical receive array.
doarx = phased.BeamscanEstimator('SensorArray',rxarray,'PropagationSpeed',c,... 'OperatingFrequency',fc,'DOAOutputPort',true,'ScanAngles',ang); Pdoarx = doarx(xr); helperPlotMultipledBPattern(ang,mag2db(abs([Pdoav Pdoarx])),[-30 0],... {'Virtual Array','Physical Array'},... 'Spatial spectrum for virtual array and physical array',{'-','--'});

Summary
In this example, we gave a brief introduction to coherent MIMO radar and the virtual array concept. We simulated the return of a MIMO radar with a 2-element transmit array and a 4-element receive array and performed direction of arrival estimation of the simulated echos of two closely spaced targets using an 8-element virtual array.
References
[1] Frank Robey, et al. MIMO Radar Theory and Experimental Results, Conference Record of the Thirty Eighth Asilomar Conference on Signals, Systems and Computers, California, pp. 300-304, 2004.
[2] Eli Brookner, MIMO Radars and Their Conventional Equivalents, IEEE Radar Conference, 2015.
[3] Sandeep Rao, MIMO Radar, Texas Instruments Application Report SWRA554, May 2017.
[4] Jian Li and Peter Stoica, MIMO Radar Signal Processing, John Wiley & Sons, 2009.