Target Localization in Active and Passive Radars
Localizing a target based on measurements from an array of spatially separated sensors with known positions has been an important problem in radar for a long time. Time of arrival (TOA) and time difference of arrival (TDOA) are commonly used measurements for localization. This example shows how to model radar networks, configure and propagate radar waveforms, and perform TOA/TDOA estimation and localization.
Introduction
Localizing a target using radars can be realized in multiple types of radar systems. For example, the most common system is a monostatic active radar system that localizes a target by actively transmitting radar waveforms and receiving the target backscattered signals using co-located and synchronized transmitter and receiver. A multistatic passive radar system can also be used to localize a target by passively receiving target backscattered signals from a separate transmit source using synchronized and distributed radars.
TOA and TDOA are commonly used measurements that provide distance information for radar localization. For a monostatic active radar system, TOA measurements are typically adopted and estimated from round-trip propagation delays between a target and monostatic radar transceivers. For a multistatic passive radar system where the separate transmit source is asynchronous to the synchronized radar receivers, the TOA measurements at radar receivers are shifted by a common unknown delay. In this case, more suitable measurements are TDOA measurements that provide the differences between the TOA measurements such that the common unknown delay is canceled. In this example, we are going to show the applications of TOA and TDOA estimation and localization in their suitable radar systems.
TOA Estimation and Localization Using Monostatic Active Radars
In this section, we consider TOA localization of a target using a monostatic active radar system, where the radars do not need to be mutually synchronized but the transmitter and the receiver at each radar are synchronized.
Scenario Configuration
We consider using 5 X-band radars built at road infrastructures with known locations to localize an unmanned aerial vehicle (UAV) target with small radar cross section (RCS).
rng('default') % RF parameters fc = 9e9; % Carrier frequency (Hz) c = physconst('LightSpeed'); % Speed of propagation (m/s) bw = 200e6; % Bandwidth (Hz) fs = bw; % Sample rate (Hz) % Tx and Rx parameters Pt = 1; % Peak power (W) Gtx = 40; % Tx antenna gain (dB) Grx = 40; % Rx antenna gain (dB) NF = 2.9; % Noise figure (dB) % Create a sensor and sensor components to simulate waveform propagation antenna = phased.IsotropicAntennaElement('BackBaffled',false); transmitter = phased.Transmitter('Gain',Gtx,'PeakPower',Pt); radiator = phased.Radiator('Sensor',antenna,'OperatingFrequency',fc); collector = phased.Collector('Sensor',antenna,'OperatingFrequency',fc); receiver = phased.Receiver('AddInputNoise',true,'Gain',Grx, ... 'NoiseFigure',NF,'SampleRate',fs); % Create a target tgtrcs = 1e-2; % Target RCS (m^2) target = phased.RadarTarget('MeanRCS',tgtrcs,'PropagationSpeed',c, ... 'OperatingFrequency',fc); % Target platform tgtpos = [30; 10; 15]; % Target position (m) tgtvel = [5; 10; 0]; % Target velocity (m/s) tgtplatform = phased.Platform('InitialPosition',tgtpos,'Velocity',tgtvel); % Radar platform radarpos = [0 -30 100 80 -40; ... 0 50 -40 30 -20; ... 0 -5 7 5 2]; % Radar positions (m) numRadar = size(radarpos,2); % Number of radars radarvel = zeros(3,numRadar); % Radar velocities (m/s) radarplatform = phased.Platform('InitialPosition',radarpos,'Velocity',radarvel);
Waveform Configuration
One of the most popular waveforms for radar systems is the frequency-modulated continuous waveform or FMCW Waveforms. FMCW waveform is widely adopted in radar systems as this technique is mature and low-cost.
% Configure FMCW waveform N = 1024; % Number of subbands (fast-time samples) M = 8; % Number of slow-time pulses freqSpacing = bw/N; % Frequency spacing (Hz) tWave = N/fs; % Waveform duration (s) fmcwWaveform = phased.FMCWWaveform('SweepTime',tWave,'SweepBandwidth',bw, ... 'SampleRate',fs,'SweepDirection','Up'); sig = fmcwWaveform()*ones(1,M);
Channel Configuration
For a monostatic active radar system, the propagation channel between each radar transceiver and the target is a two-way channel. We do not consider mutual radar interference in this example.
% Create a two-way free-space propagation channel channel = phased.FreeSpace('PropagationSpeed',c,'OperatingFrequency',fc, ... 'SampleRate',fs,'TwoWayPropagation',true);
Radar Data Cube
We first obtain the Radar Data Cube for each monostatic active radar. In this example, a radar data cube is defined as the complex-valued baseband samples arranged in a N-by-M matrix, where N is the number of fast-time samples and M is the number of slow-time pulses.
% Reference signal refsig = sig; % Radar data cubes for all radars X = cell(1,numRadar); % Transmitted signal txsig = transmitter(sig); for idxRadar = 1:numRadar % Initialize estimated channel x = complex(zeros(size(sig))); % Transceiver chain for m = 1:M % Update radar and target positions [radar_pos,radar_vel] = radarplatform(tWave); [tgt_pos,tgt_vel] = tgtplatform(tWave); % Calculate the transmit angle [~,txang] = rangeangle(tgt_pos,radar_pos(:,idxRadar)); % Radiate signal towards the receiver radtxsig = radiator(txsig(:,m),txang); % Propagate the signal chansig = channel(radtxsig,radar_pos(:,idxRadar),tgt_pos, ... radar_vel(:,idxRadar),tgt_vel); % Reflect the signal off the target tgtsig = target(chansig); % Calculate the receive angle [~,rxang] = rangeangle(radar_pos(:,idxRadar),tgt_pos); % Collect signal at the receive antenna rxsig = collector(tgtsig,rxang); % Receive signal at the receiver x(:,m) = receiver(rxsig); end % Obtain radar data cube for the current radar dechirpsig = dechirp(x,refsig(:,1)); X{idxRadar} = conj(dechirpsig); % Reset platform for the next radar reset(radarplatform); reset(tgtplatform); end
TOA Estimation and Localization
After obtaining the radar data cubes, the next step is to obtain the TOA measurements. In the following, we use phased.TOAEstimator system object to estimate TOA by configuring the 'Measurement' property to 'TOA'. The spectrum analysis method can be configured as either FFT or MUSIC. We can change the spectrum analysis method to see its impact on the TOA localization accuracy shown at the end of this section.
% Spectrum analysis method spectrumMethod ="FFT"; % Configure TOA estimator if strcmp(spectrumMethod,'FFT') toaEstimator = phased.TOAEstimator('PropagationSpeed',c, ... 'Measurement','TOA','SpectrumMethod',spectrumMethod, ... 'VarianceOutputPort',true); else % 'MUSIC' toaEstimator = phased.TOAEstimator('PropagationSpeed',c, ... 'Measurement','TOA','SpectrumMethod',spectrumMethod, ... 'VarianceOutputPort',true, ... 'ForwardBackwardAveraging',true,'SpatialSmoothing',ceil(N/2)); %#ok<UNRCH> end % TOA estimation [Y,var] = toaEstimator(X,freqSpacing);
Viewing the TOA spectrum can provide us better insights on how well TOA is estimated for each radar. In the ideal case, the first peak on the TOA spectrum is picked as the TOA estimate. We can view the TOA estimation result for a radar using plotTOASpectrum.
% Plot TOA spectrum figure plotTOASpectrum(toaEstimator,freqSpacing,'AnchorIndex',1,'MaxDelay',500e-9);
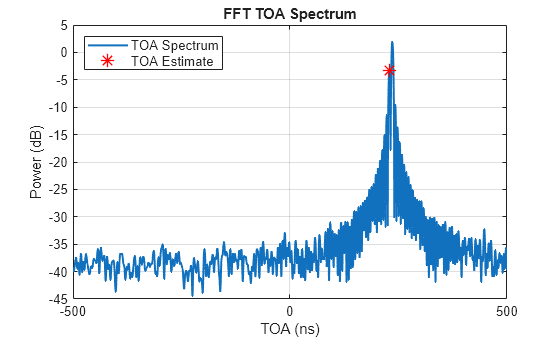
Once we have the one-way propagation TOA estimates, the one-way propagation TOA estimation variances, and known radar positions, we can use toaposest to localize the target. As the obtained TOA estimates are the round-trip propagation delay estimates, we divide the round-trip propagation delay estimates by 2 to obtain one-way propagation TOA estimates and divide the estimated TOA variances by 4 to obtain estimated one-way propagation TOA estimation variances.
% Single-trip TOA and TOA variance Ysingle = Y/2; varsingle = var/4; % Obtain TOA position estimate tgtposest = toaposest(Ysingle,varsingle,radarpos);
We visualize the performance of the TOA localization below.
% View TOA position estimate
helperPlotTOAPositions(c,Ysingle,tgtposest,radarpos,tgtpos);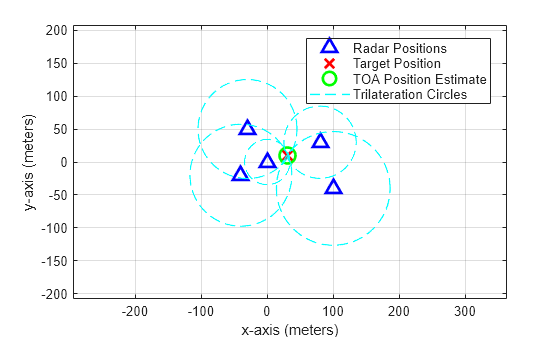
We can also check the accuracy of the TOA localization using root mean squared error (RMSE).
% RMSE of the TOA position estimate RMSE = rmse(tgtposest,tgtpos); disp(['RMS Localization error = ', num2str(RMSE), ' meters.'])
RMS Localization error = 0.85517 meters.
TDOA Estimation and Localization Using Multistatic Passive Radars
In this section, we consider TDOA localization of a target using a multistatic passive radar system, where the distributed radar receivers are mutually synchronized and passively receive backscattered target signals originated from a separate asynchronous transmit source with unknown waveform. For a passive radar system, the separate transmit source can be another radar station, a cellular base station, a TV transmitter tower, etc.
Scenario Configuration
We consider using 5 ground radar receivers with known locations to localize an aircraft target using backscattered signals from a separate asynchronous DBS TV transmitter tower operating at the Ku-band.
% RF parameters fc = 12e9; % Carrier frequency (Hz) c = physconst('LightSpeed'); % Speed of propagation (m/s) bw = 100e6; % Bandwidth (Hz) fs = bw; % Sample rate (Hz) % Tx and Rx parameters Pt = 10; % Peak power (W) Gtx = 40; % Tx antenna gain (dB) Grx = 40; % Rx antenna gain (dB) NF = 2.9; % Noise figure (dB) % Create a sensor and sensor components to simulate waveform propagation antenna = phased.IsotropicAntennaElement('BackBaffled',false); transmitter = phased.Transmitter('Gain',Gtx,'PeakPower',Pt); radiator = phased.Radiator('Sensor',antenna,'OperatingFrequency',fc); collector = phased.Collector('Sensor',antenna,'OperatingFrequency',fc); receiver = phased.Receiver('AddInputNoise',true,'Gain',Grx, ... 'NoiseFigure',NF,'SampleRate',fs); % Create a target tgtrcs = 1000; % Target RCS (m^2) target = phased.RadarTarget('MeanRCS',tgtrcs,'PropagationSpeed',c, ... 'OperatingFrequency',fc); % Target platform tgtpos = [80; 40; 110]; % Target position (m) tgtvel = [50; 40; 0]; % Target velocity (m/s) tgtplatform = phased.Platform('InitialPosition',tgtpos,'Velocity',tgtvel); % Radar platform radarpos = [0 300 100 200 150; ... 0 50 -200 300 100; ... 0 -10 10 5 20]; % Radar positions (m) numRadar = size(radarpos,2); % Number of radars radarvel = zeros(3,numRadar); % Radar velocities (m/s) radarplatform = phased.Platform('InitialPosition',radarpos,'Velocity',radarvel); % Separate transmitter platform txpos = [-150; -100; 50]; % Transmitter position (m) txvel = [0; 0; 0]; % Transmitter velocity (m/s) txplatform = phased.Platform('InitialPosition',txpos,'Velocity',txvel);
Waveform Configuration
Phase-Coded Waveforms is another type of radar waveform. Multiple phase codes can be chosen in the phase coded waveform, such as Zadoff-Chu code, Barker code, maximum length sequence (MLS), etc. In the following, we configure a phase-code waveform with MLS as its phase code.
% Configure phase-coded waveform N = 1024; % Number of subbands M = 8; % Number of slow-time pulses numChip = 2^nextpow2(N)-1; % Number of chips in one phase-coded waveform tchip = 1/bw; % Chip duration (s) tWave = numChip * tchip; % Modulation period (s) prf = 1/tWave; % PRF (1/s) % Configure the phase coded waveform as the maximum length sequence pmcwWaveform = phased.PhaseCodedWaveform('Code','Maximum Length Sequence', ... 'SampleRate',fs,'NumChips',numChip,'ChipWidth',tchip,'PRF',prf); sig = pmcwWaveform()*ones(1,M);
Channel Configuration
A multistatic radar system basically contains two one-way channels. The first channel is the channel from the separate transmit source to the target, and the second channel is the channel from the target to each radar. We specify the two channels below.
% One-way free-space propagation channel from the radar transmitter tower to the target txchannel = phased.FreeSpace('PropagationSpeed',c,'OperatingFrequency',fc, ... 'SampleRate',fs,'TwoWayPropagation',false); % One-way free-space propagation channel from the target to each radar receiver rxchannel = clone(txchannel);
Radar Data Cube
In the following code, we show how to obtain the multistatic radar data cube when phase-coded waveform is used.
% Radar data cubes for all radars X = complex(zeros([size(sig),numRadar])); % Transmitted signal txsig = transmitter(sig); for idxRadar = 1:numRadar % Initialize estimated radar data cube at a radar x = complex(zeros(size(sig))); % Transceiver chain for m = 1:M % Update separate transmitter, radar and target positions [tx_pos,tx_vel] = txplatform(tWave); [radar_pos,radar_vel] = radarplatform(tWave); [tgt_pos,tgt_vel] = tgtplatform(tWave); % Calculate the transmit angle [~,txang] = rangeangle(tgt_pos,tx_pos); % Radiate signal towards the receiver radtxsig = radiator(txsig(:,m),txang); % Propagate the signal from the transmitter to the target txchansig = txchannel(radtxsig,tx_pos,tgt_pos, ... tx_vel,tgt_vel); % Reflect the signal off the target tgtsig = target(txchansig); % Propagate the signal from the target to each radar rxchansig = rxchannel(tgtsig,radar_pos(:,idxRadar),tgt_pos, ... radar_vel(:,idxRadar),tgt_vel); % Calculate the receive angle [~,rxang] = rangeangle(radar_pos(:,idxRadar),tgt_pos); % Collect signal at the receive antenna rxsig = collector(rxchansig,rxang); % Receive signal at the receiver x(:,m) = receiver(rxsig); end % Obtain radar data cube for the current radar X(:,:,idxRadar) = x; % Reset platform for the next radar reset(txplatform); reset(radarplatform); reset(tgtplatform); end
TDOA Estimation and Localization
After obtaining the multistatic passive radar data cube, the next step is to obtain the TDOA measurements. In the following, we use phased.TDOAEstimator system object to estimate TDOAs between different radar pairs based on the generalized cross-correlation (GCC) phase transform (PHAT) algorithm.
% Configure TDOA estimator tdoaEstimator = phased.TDOAEstimator('SampleRateSource','Input port', ... 'VarianceOutputPort',true); % TDOA estimation [Y,var] = tdoaEstimator(X,fs);
Viewing the TDOA spectrum can provide us better insights on how well TDOA is estimated for each radar pair. We can view the TDOA estimation result for a radar pair using plotTDOASpectrum.
% Plot TDOA spectrum figure plotTDOASpectrum(tdoaEstimator,'AnchorPairIndex',1,'MaxDelay',1000e-9);
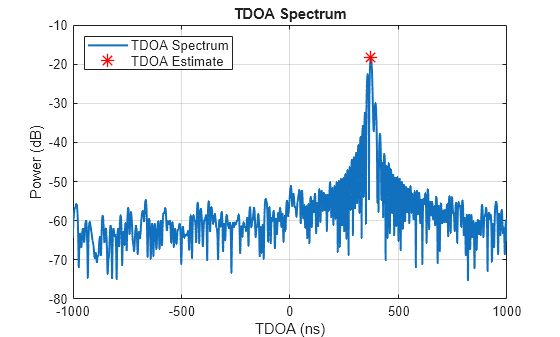
Once we have the TDOA estimates, the TDOA estimation variances, and known radar positions, we can use tdoaposest to do TDOA localization.
% Obtain TDOA position estimate
tgtposest = tdoaposest(Y,var,radarpos);We visualize the performance of the TDOA localization below.
% View TDOA position estimate
helperPlotTDOAPositions(c,Y,tgtposest,radarpos,tgtpos,txpos)
We can also check the accuracy of the TDOA localization using RMSE.
% RMSE of the TDOA position estimate RMSE = rmse(tgtposest,tgtpos); disp(['RMS Localization error = ', num2str(RMSE), ' meters.'])
RMS Localization error = 1.5428 meters.
Summary
In this example, we considered localization of a target in two common radar systems. The first system is a network of monostatic active radars adopting FMCW waveform. We showed how to perform TOA estimation and TOA localization using phased.TOAEstimator and toaposest. The second system is a network of multistatic passive radars adopting phase-coded waveform. We showed how to perform TDOA estimation and TDOA localization using phased.TDOAEstimator and tdoaposest.
References
[1] J. Lee, M. Park, I. Eo and B. Koo, "An X-Band FMCW Radar for Detection and Tracking of Miniaturized UAVs," 2017 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 2017, pp. 1844-1845
[2] Hugh Griffiths and Christopher Baker, An Introduction to Passive Radar, Second Edition, 2022
See Also
phased.TOAEstimator | phased.TDOAEstimator | toaposest | tdoaposest | plotTDOASpectrum | plotTOASpectrum