Clarke Transform
Implement abc to αβ0 transform
Libraries:
Simscape /
Electrical /
Control /
Mathematical Transforms
Description
The Clarke Transform block converts the time-domain components of a three-phase system in an abc reference frame to components in a stationary ɑβ0 reference frame. The block can preserve the active and reactive powers with the powers of the system in the abc reference frame by implementing a power invariant version of the Clarke transform. For a balanced system, the zero component is equal to zero.
If you have a license for Motor Control Blockset™ toolbox, you can use this block for embedded implementation. Use the
Number of inputs parameter to specify either two or three
inputs. When you set the Number of inputs parameter to
Two inputs, the block accepts two signals out of the
three phases (abc), automatically calculates the
third signal, and outputs the corresponding components in the αβ reference frame. (since R2025a)
The figures show:
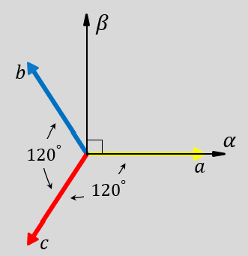
The direction of the magnetic axes of the stator windings in the abc reference frame and the stationary ɑβ0 reference frame
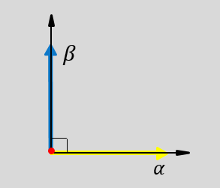
Equivalent ɑ, β, and zero components in the stationary reference frame
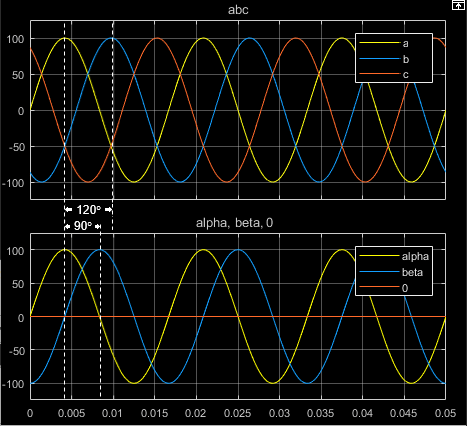
The time-response of the individual components of equivalent balanced abc and ɑβ0 systems
Equations
The block implements the Clarke transform as
where:
a, b, and c are the components of the three-phase system in the abc reference frame.
α and β are the components of the two-axis system in the stationary reference frame.
0 is the zero component of the two-axis system in the stationary reference frame.
The block implements the power invariant version of the Clarke transform as
Examples
Ports
Input
Output
Parameters
References
[1] Krause, P., O. Wasynczuk, S. D. Sudhoff, and S. Pekarek. Analysis of Electric Machinery and Drive Systems. Piscatawy, NJ: Wiley-IEEE Press, 2013.