FEM-Parameterized PMSM

Permanent magnet synchronous motor defined in terms of magnetic flux linkage

Library:
Simscape / Electrical / Electromechanical / Permanent Magnet

Description

The FEM-Parameterized PMSM block implements a model of a permanent magnet synchronous motor (PMSM) defined in terms of magnetic flux linkage. You parameterize the block by providing tabulated data of motor magnetic flux as a function of current and rotor angle. This is the way third-party magnetic finite-element method (FEM) packages usually export flux information. Because of the tabulated form, the flux can vary in a nonlinear way on both rotor angle and current. You can therefore use this block to model PMSM with trapezoidal back-emf profile, sometimes called brushless DC motor, as well as regular PMSM.

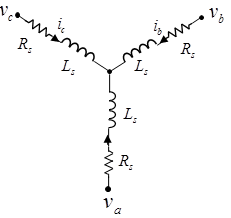
The figure shows the equivalent circuit for a wye-connected PMSM. The rotor angle is zero when the permanent magnet flux aligns with the A-phase magnetic axis.

In practice, the flux linking each of the three windings depends on all three currents and rotor angle. Tabulating flux as a function of four independent variables might lead to simulation inefficiency and significant memory requirements to manage the data. The block, therefore, lets you select between the following parameterization methods for flux and torque:

2-D partial derivative data — 2-D table lookup, with options to tabulate in terms of current and rotor angle, or in terms of d-axis and q-axis currents. The first option assumes constant mutual inductance and supports nonsinusoidal back emf profiles. The second option assumes a sinusoidal back emf and captures saturation effects for interior PMSMs (IPMSMs).
3-D partial derivative data — 3-D table lookup, based on direct current, quadrature current, and rotor angle. You provide the flux lookup data for the a phase. The block uses Park transform to map the three stator winding currents to direct and quadrature currents. This method reduces the data complexity, as compared to the 4-D table lookup, and therefore results in improved simulation performance.
4-D partial derivative data — 4-D table lookup, based on the three stator winding currents and the rotor angle. You provide the flux lookup data for the a phase. This model has the best fidelity of the three, but also is the most costly in terms of simulation performance and memory requirements.
3-D flux linkage data — 3-D table lookup, based on the flux linkage data. You can provide the flux linkage data in a variety of formats. The block uses Park transform to map the three stator winding currents to direct and quadrature currents. This method reduces the data complexity, as compared to the 4-D table lookup, and therefore results in improved simulation performance.

By default, all of the block variants implement a wye-wound configuration for the stator windings. However, it is possible to switch to a delta-wound configuration, selectable using the Winding type parameter. When in the delta-wound configuration, the a phase is connected between ports a and b, the b phase between ports b and c and the c phase between ports c and a.

To access these parameterization methods, right-click the block in your model, select Simscape > Block choices, and then select the desired block variant, with or without thermal ports. By default, the thermal ports are not exposed. For more information, see Thermal Ports.

2-D Data Model with Constant Mutual Inductance

In this 2-D flux data model, the flux linking each winding is assumed to depend nonlinearly only on the current in that same winding, plus the rotor angle. In practice, this is a reasonable assumption for many permanent magnet synchronous motors; however, it is less accurate for switched reluctance motors. Given this assumption, the fluxes in the three windings are:

$[\begin{matrix} ϕ_{a} \\ \begin{array}{l} ϕ_{b} \\ ϕ_{c} \end{array} \end{matrix}] = [\begin{matrix} 0 & - M_{s} & - M_{s} \\ - M_{s} & 0 & - M_{s} \\ - M_{s} & - M_{s} & 0 \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}] + [\begin{matrix} ϕ (i_{a}, θ_{r}) \\ \begin{array}{l} ϕ (i_{b}, θ_{r} - 2 π / (3 N)) \\ ϕ (i_{c}, θ_{r} - 4 π / (3 N)) \end{array} \end{matrix}]$

where $ϕ (θ_{r}, i_{a})$ is the flux linkage for the A-phase winding as a function of rotor angle and A-phase current. Θ_r = 0 corresponds to the rotor d-axis aligning with the A-phase positive magnetic flux direction. M_s is the stator-stator mutual inductance.

For improved numerical performance, the equations implemented in the block actually work with the partial derivatives of flux linkage with respect to current, $\partial ϕ (i, θ_{r}) / \partial i$ , and rotor angle, $\partial ϕ (i, θ_{r}) / \partial θ_{r}$ , rather than the flux directly. If your FEM package does not export these partial derivatives, you can determine them using a MATLAB^® script. See the Solenoid Parameterized with FEM Data example model and its supporting MATLAB script for an example of how to do this.

The electrical equations for the block, defined in terms of flux partial derivatives, are:

$\begin{array}{l} v_{a} = \frac{\partial ϕ}{\partial i_{a}} \frac{d i_{a}}{d t} + \frac{\partial ϕ}{\partial θ_{r}} \frac{d θ_{r}}{d t} - M_{s} (\frac{d i_{b}}{d t} + \frac{d i_{c}}{d t}) + R_{s} i_{a} \\ v_{b} = \frac{\partial ϕ}{\partial i_{b}} \frac{d i_{b}}{d t} + \frac{\partial ϕ}{\partial θ_{r}} \frac{d θ_{r}}{d t} - M_{s} (\frac{d i_{a}}{d t} + \frac{d i_{c}}{d t}) + R_{s} i_{b} \\ v_{c} = \frac{\partial ϕ}{\partial i_{c}} \frac{d i_{c}}{d t} + \frac{\partial ϕ}{\partial θ_{r}} \frac{d θ_{r}}{d t} - M_{s} (\frac{d i_{a}}{d t} + \frac{d i_{b}}{d t}) + R_{s} i_{c} \end{array}$

where

v_a, v_b, v_c are the voltages applied to the A, B, and C stator windings.
i_a, i_b, i_c are the stator currents in each of the three windings.
R_s is the resistance of each of the stator windings.
M_s is the stator-stator mutual inductance.
$\partial ϕ / \partial i_{a}, \partial ϕ / \partial i_{b}, \partial ϕ / \partial i_{c}$ are the partial derivatives of flux linkage with respect to stator current in each of the three windings.
$\partial ϕ / \partial θ_{r}$ is the partial derivative of flux linkage with respect to rotor angle.

The block can automatically calculate the torque matrix from the flux information that you provide. Alternatively, you can set the Calculate torque matrix? parameter to No and directly specify the torque as a function of current and rotor angle. See the FEM-Parameterized Rotary Actuator block reference page for more information.

2-D Data Model with Sinusoidal Back EMF

In this 2-D flux data model, the flux linking each winding is assumed to depend nonlinearly on all stator winding currents, plus it is assumed that the permanent magnet flux linkage is sinusoidal. Interior magnet PMSMs (or IPMSMs) usually fit this assumption well. The equations are:

$[\begin{matrix} ϕ_{d} \\ ϕ_{q} \end{matrix}] = [\begin{matrix} L_{d} (i_{d}, i_{q}) \\ L_{q} (i_{d}, i_{q}) \end{matrix}] [\begin{matrix} i_{d} \\ i_{q} \end{matrix}] + [\begin{matrix} ϕ_{m} (i_{d}, i_{q}) \end{matrix}]$

$T = \frac{3}{2} N (i_{q} (i_{d} L_{d} (i_{d}, i_{q}) + ϕ_{m} (i_{d}, i_{q})) - i_{d} i_{q} L_{q} (i_{d}, i_{q}))$

where

i_d and i_q are the d-axis and q-axis currents, respectively.
ϕ_d and ϕ_q are the d-axis and q-axis flux linkages, respectively.
ϕ_m is the permanent magnet flux linkage.
L_d and L_q are the d-axis and q-axis inductances, respectively. They are assumed to depend on the d-axis and q-axis currents.
N is the number of pole pairs.
T is the electrical torque.

3-D Partial Derivative Data Model Using Park Transform

Working with four-dimensional data has both a simulation performance cost and a memory cost. To reduce the table dimension to three-dimensional, the 3-D data model uses Park transform to map the three currents to direct and quadrature currents:

$[\begin{matrix} i_{d} \\ i_{q} \end{matrix}] = \frac{2}{3} [\begin{matrix} \cos θ_{e} & \cos (θ_{e} - \frac{2 π}{3}) & \cos (θ_{e} + \frac{2 π}{3}) \\ - \sin θ_{e} & - \sin (θ_{e} - \frac{2 π}{3}) & - \sin (θ_{e} + \frac{2 π}{3}) \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}]$

In the general case, Park transform maps to direct, quadrature, and zero-sequence currents. However, the zero-sequence current is typically small under normal operating conditions. Therefore, the model neglects the dependence of the flux linkage terms on zero-sequence current, and determines the flux linkage in terms of just direct and quadrature currents plus rotor angle. The flux equation for the 3-D data model is:

$[\begin{matrix} ϕ_{a} \\ \begin{array}{l} ϕ_{b} \\ ϕ_{c} \end{array} \end{matrix}] = [\begin{matrix} ϕ (i_{d}, i_{q}, θ_{r}) \\ \begin{array}{l} ϕ (i_{d}, i_{q}, θ_{r} - 2 π / (3 N)) \\ ϕ (i_{d}, i_{q}, θ_{r} - 4 π / (3 N)) \end{array} \end{matrix}]$

The electrical equations for the block are also defined in terms of flux partial derivatives, similar to the 4-D data model. You can calculate 3-D flux linkage partial derivative data from 4-D flux linkage data using ee_calculateFluxPartialDerivatives.

4-D Partial Derivative Data Model

The flux linking each of the windings is a function of the current in that winding, the currents in the other two windings, and the rotor angle. For full accuracy, the 4-D flux data model assumes that the flux linkage is a function of the three currents and the rotor angle, therefore performing four-dimensional table lookups. The flux equation is:

$[\begin{matrix} ϕ_{a} \\ \begin{array}{l} ϕ_{b} \\ ϕ_{c} \end{array} \end{matrix}] = [\begin{matrix} ϕ (i_{a}, i_{b}, i_{c}, θ_{r}) \\ \begin{array}{l} ϕ (i_{b}, i_{c}, i_{a}, θ_{r} - 2 π / (3 N)) \\ ϕ (i_{c}, i_{a}, i_{b}, θ_{r} - 4 π / (3 N)) \end{array} \end{matrix}]$

where

ϕ_a, ϕ_b, ϕ_c are the flux linkages for the A, B, and C stator windings.
i_a, i_b, i_c are the stator currents in each of the three windings.
Θ_r is the rotor angle. Θ_r = 0 corresponds to the case where the permanent magnet flux is aligned with the A-phase stator winding flux.
N is the number of pole pairs.

Flux linkage data is assumed cyclic with Θ_r. If, for example, the motor has six pole pairs, then the range for the data is 0 ≤ Θ_r ≤ 60°. You must provide data both at 0 and 60 degrees, and because the data is cyclic, the flux linkage partial derivatives must be the same at these two end points.

The torque equation is:

$τ = T (i_{a}, i_{b}, i_{c}, θ_{r})$

The 4-D data model does not have an option for the block to determine torque from flux linkage. Because of the increased numerical overhead in the 4-D case, it is better to precalculate the torque just once, rather than calculate it every time you run the simulation.

For improved numerical performance, the equations implemented in the block actually work with the partial derivatives of flux linkage with respect to the three currents and the rotor angle, rather than the flux directly. If your FEM package does not export these partial derivatives, you can determine them using ee_calculateFluxPartialDerivatives.

The electrical equations for the block, defined in terms of flux partial derivatives, are:

$\begin{array}{l} v_{a} = \frac{\partial ϕ_{a}}{\partial i_{a}} \frac{d i_{a}}{d t} + \frac{\partial ϕ_{a}}{\partial i_{b}} \frac{d i_{b}}{d t} + \frac{\partial ϕ_{a}}{\partial i_{c}} \frac{d i_{c}}{d t} + \frac{\partial ϕ_{a}}{\partial θ_{r}} \frac{d θ_{r}}{d t} + R_{s} i_{a} \\ v_{b} = \frac{\partial ϕ_{b}}{\partial i_{a}} \frac{d i_{a}}{d t} + \frac{\partial ϕ_{b}}{\partial i_{b}} \frac{d i_{b}}{d t} + \frac{\partial ϕ_{b}}{\partial i_{c}} \frac{d i_{c}}{d t} + \frac{\partial ϕ_{b}}{\partial θ_{r}} \frac{d θ_{r}}{d t} + R_{s} i_{b} \\ v_{c} = \frac{\partial ϕ_{c}}{\partial i_{a}} \frac{d i_{a}}{d t} + \frac{\partial ϕ_{c}}{\partial i_{b}} \frac{d i_{b}}{d t} + \frac{\partial ϕ_{c}}{\partial i_{c}} \frac{d i_{c}}{d t} + \frac{\partial ϕ_{c}}{\partial θ_{r}} \frac{d θ_{r}}{d t} + R_{s} i_{c} \end{array}$

where

v_a, v_b, v_c are the voltages applied to the A, B, and C stator windings.
i_a, i_b, i_c are the stator currents in each of the three windings.
R_s is the resistance of each of the stator windings.

3-D Flux Linkage Data Models

The 3-D flux linkage data options let you work with raw flux linkage data exported from your finite-element (FE) motor design tool. This is in contrast to the 3-D partial derivative data options, for which you need to determine the partial derivatives. You can provide flux linkage data in a variety of formats, to support different FE tool conventions:

Tabulate DQ-axes flux linkage data or A-phase flux linkage data — Some tools support working with flux linkage resolved into direct (D) and quadrature (Q) axes. An advantage of this approach is that data for rotor angles in the range 0 to 360/N/3 degrees is required (where N is the number of pole pairs). Other tools work directly with A-, B-, and C-phase flux linkages, and for this you can import just the A-phase flux linkage, for which the rotor angle range must be in the range 0 to 360/N degrees. The implicit assumption of importing just the A-phase data is that the B and C phase data is the same except shifted in phase.
Tabulate using cartesian or polar current coordinates — Cartesian tabulation implies the flux linkage is tabulated in terms of D-axis current and Q-axis current (plus rotor angle). Alternatively, polar tabulation involves tabulating flux linkages in terms of current magnitude, current advance angle relative to the Q-axis, and rotor angle. The advantage of polar coordinates is that it more naturally reflects the permitted operating currents, thereby avoiding unused table data points.

These conventions result in four Flux linkage data format parameterization options:

D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)

Besides selecting the flux linkage data format used by your FE tool, you have to select the version of Park transform used by the tool. The four conventions are described below and correspond to the four options for the Park’s convention for tabulated data drop-down menu.

Note

When looking at logged values for D- and Q-axis currents, keep in mind that for each of these options, the format is converted, as needed, so that internally the FEM-Parameterized PMSM block consistently uses Option 1.

Option 1. Q leads D, rotor angle measured from A-phase to D-axis

This is the Park’s convention used internally by Simscape™ Electrical™ motor and machine blocks. All other options are converted into this format.

N: number of pole pairs
θ_r: rotor angle
i_d, i_q: D-axis and Q-axis currents
i_p: Current magnitude = $\sqrt{i_{d}^{2} + i_{q}^{2}}$
β: Current advance angle = $\tan^{- 1} (- i_{d} / i_{q})$

Corresponding Park transform is

$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \cos (N θ_{r}) & \cos (N θ_{r} - \frac{2 π}{3}) & \cos (N θ_{r} + \frac{2 π}{3}) \\ - \sin (N θ_{r}) & - \sin (N θ_{r} - \frac{2 π}{3}) & - \sin (N θ_{r} + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}]$

where i_a, i_b, and i_c are the A-phase, B-phase, and C-phase currents, respectively.

Option 2. Q leads D, rotor angle measured from A-phase to Q-axis

N: number of pole pairs
θ_r: rotor angle
i_d, i_q: D-axis and Q-axis currents
i_p: Current magnitude = $\sqrt{i_{d}^{2} + i_{q}^{2}}$
β: Current advance angle = $\tan^{- 1} (- i_{d} / i_{q})$

Corresponding Park transform is

$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \sin (N θ_{r}) & \sin (N θ_{r} - \frac{2 π}{3}) & \sin (N θ_{r} + \frac{2 π}{3}) \\ \cos (N θ_{r}) & \cos (N θ_{r} - \frac{2 π}{3}) & \cos (N θ_{r} + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}]$

where i_a, i_b, and i_c are the A-phase, B-phase, and C-phase currents, respectively.

Option 3. D leads Q, rotor angle measured from A-phase to D-axis

N: number of pole pairs
θ_r: rotor angle
i_d, i_q: D-axis and Q-axis currents
i_p: Current magnitude = $\sqrt{i_{d}^{2} + i_{q}^{2}}$
β: Current advance angle = $\tan^{- 1} (- i_{d} / i_{q})$

Corresponding Park transform is

$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \cos (N θ_{r}) & \cos (N θ_{r} - \frac{2 π}{3}) & \cos (N θ_{r} + \frac{2 π}{3}) \\ \sin (N θ_{r}) & \sin (N θ_{r} - \frac{2 π}{3}) & \sin (N θ_{r} + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}]$

where i_a, i_b, and i_c are the A-phase, B-phase, and C-phase currents, respectively.

Option 4. D leads Q, rotor angle measured from A-phase to Q-axis

N: number of pole pairs
θ_r: rotor angle
i_d, i_q: D-axis and Q-axis currents
i_p: Current magnitude = $\sqrt{i_{d}^{2} + i_{q}^{2}}$
β: Current advance angle = $\tan^{- 1} (- i_{d} / i_{q})$

Corresponding Park transform is

$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} - \sin (N θ_{r}) & - \sin (N θ_{r} - \frac{2 π}{3}) & - \sin (N θ_{r} + \frac{2 π}{3}) \\ \cos (N θ_{r}) & \cos (N θ_{r} - \frac{2 π}{3}) & \cos (N θ_{r} + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} i_{a} \\ \begin{array}{l} i_{b} \\ i_{c} \end{array} \end{matrix}]$

where i_a, i_b, and i_c are the A-phase, B-phase, and C-phase currents, respectively.

Calculating Iron Losses

The FEM-Parameterized PMSM block models iron losses according to the parameterization methods you choose for flux and torque.

For the 2-D partial derivative data, 3-D partial derivative data, and 4-D partial derivative data options, with or without thermal ports, the iron loss model is based on the work of Mellor [1]. Iron losses are divided into two terms, one representing the main magnetizing path, and the other representing the cross-tooth tip path that becomes active during field weakened operation.

The term representing the main magnetizing path depends on the induced RMS stator voltage, $V_{m_{r m s}}^{}$ :

$P_{O C} (V_{m_{r m s}}^{}) = \frac{a_{h}}{k} V_{m_{r m s}}^{} + \frac{a_{j}}{k^{2}} V_{m_{r m s}}^{2} + \frac{a_{e x}}{k^{1.5}} V_{m_{r m s}}^{1.5}$

This is the dominant term during no-load operation. k is the back emf constant relating RMS volts per Hz. It is defined as $k = V_{m_{r m s}}^{} / f$ , where f is the electrical frequency. The first term on the right-hand side is the magnetic hysteresis loss, the second is the eddy current loss and the third is the excess loss. The three coefficients appearing on the numerators are derived from the values that you provide for the open-circuit hysteresis, eddy, and excess losses.

The term representing the cross-tooth tip path becomes important when a demagnetizing field is set up and can be determined from a finite element analysis short-circuit test. It depends on the RMS emf associated with the cross-tooth tip flux, $V_{d_{r m s}}^{*}$ :

$P_{S C} (V_{d_{r m s}}^{*}) = \frac{b_{h}}{k} V_{d_{r m s}}^{*} + \frac{b_{j}}{k^{2}} V_{d_{r m s}}^{* 2} + \frac{b_{e x}}{k^{1.5}} V_{d_{r m s}}^{* 1.5}$

The three numerator terms are derived from the values you provide for the short-circuit hysteresis, eddy, and excess losses.

Steinmetz parameterization method

For the 3-D flux linkage data with or without thermal ports, you can also model the iron losses based on the Steinmetz equation. The Steinmetz method scales for different motor speeds or electrical frequencies so that iron loss data is only required as function of motor currents.

If you set the Iron losses modeling parameter to Specify open and short circuit loss data (permanent magnet motors only), the block uses the Steinmetz method, but assumes constant coefficients and no dependency on peak current and current phase advance. Select this option if you have dyno measurements or if you perform an FE analysis to get the iron losses from just open-circuit and short-circuit simulations.

Conversely, if you set the Flux linkage data format parameter to either D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) or A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) , then the block tabulated the coefficients with the Peak current magnitude vector, I and Current advance angle vector, B parameters, so that the iron losses are given by:

$\begin{array}{l} P_{r o t o r} (f) = k_{h r} (I_{p}, β) f + k_{J r} (I_{p}, β) f^{2} + k_{e r} (I_{p}, β) f^{1.5} \\ P_{s t a t o r} (f) = k_{h s} (I_{p}, β) f + k_{J s} (I_{p}, β) f^{2} + k_{e s} (I_{p}, β) f^{1.5} \end{array}$

where:

f is the electrical frequency, in Hz.
k_hr(I_p,β) is the Rotor hysteresis loss coefficient, k_hr(I,B).
k_Jr(I_p,β) is the Rotor eddy current loss coefficient, k_Jr(I,B).
k_er(I_p,β) is the Rotor excess current loss coefficient, k_er(I,B).
k_hs(I_p,β) is the Stator hysteresis loss coefficient, k_hs(I,B).
k_Js(I_p,β) is the Stator eddy current loss coefficient, k_Js(I,B).
k_es(I_p,β) is the Stator excess current loss coefficient, k_es(I,B).

Similarly, if you set the Flux linkage data format parameter to either D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta) or A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta), then the iron losses are given by:

$\begin{array}{l} P_{r o t o r} (f) = k_{h r} (i_{D}, i_{Q}) f + k_{J r} (i_{D}, i_{Q}) f^{2} + k_{e r} (i_{D}, i_{Q}) f^{1.5} \\ P_{s t a t o r} (f) = k_{h s} (i_{D}, i_{Q}) f + k_{J s} (i_{D}, i_{Q}) f^{2} + k_{e s} (i_{D}, i_{Q}) f^{1.5} \end{array}$

where:

k_hr(i_D,i_Q) is the Rotor hysteresis loss coefficient, k_hr(iD,iQ).
k_Jr(i_D,i_Q) is the Rotor eddy current loss coefficient, k_Jr(iD,iQ).
k_er(i_D,i_Q) is the Rotor excess current loss coefficient, k_er(iD,iQ).
k_hs(i_D,i_Q) is the Stator hysteresis loss coefficient, k_hs(iD,iQ).
k_Js(i_D,i_Q) is the Stator eddy current loss coefficient, k_Js(iD,iQ).
k_es(i_D,i_Q) is the Stator excess current loss coefficient, k_es(iD,iQ).

Select this option only in conjunction with a motor design tool that can calculate the coefficients. For more information, see the Import IPMSM Flux Linkage Data from Motor-CAD example.

Thermal Ports

The block has four optional thermal ports, one for each of the three windings and one for the rotor. These ports are hidden by default. To expose the thermal ports, right-click the block in your model, select Simscape > Block choices, and then select the desired block variant with thermal ports: 2-D partial derivative data | Show thermal port, 3-D partial derivative data | Show thermal port, 4-D partial derivative data | Show thermal port, or 3-D flux linkage data | Show thermal port. This action displays the thermal ports on the block icon, and exposes the Temperature Dependence and Thermal Port parameters. These parameters are described further on this reference page.

Use the thermal ports to simulate the effects of copper resistance and iron losses that convert electrical power to heat. For more information on using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.

Assumptions and Limitations

This block has the following limitations:

For the 2-D data model, the stator-stator mutual inductance, defined by the Stator mutual inductance, Ms parameter value, is constant during simulation and does not vary with rotor angle. This means that the block is suitable for modeling most PMSM and brushless DC motors, but not switched reluctance motors.
The 3-D and 4-D data models assume symmetry, so that the flux linkage dependency on currents and rotor angle for windings B and C can be determined from that for winding A.
For the 4-D data model, consider memory requirements when fixing the independent parameter values (three currents and rotor angles). The linear interpolation option uses less memory, but the smooth interpolation option is more accurate for a given independent parameter spacing.
The iron losses model assumes sinusoidal currents.

Ports

Conserving

expand all

`a` — A-phase connection
electrical

Electrical conserving port associated with the A-phase connection.

`b` — B-phase connection
electrical

Electrical conserving port associated with the B-phase connection.

`c` — C-phase connection
electrical

Electrical conserving port associated with the C-phase connection.

`n` — Neutral phase
electrical

Electrical conserving port associated with the neutral phase.

Dependencies

To expose this port, right-click the block in your model, select Simscape > Block choices, and then either:

Choose the desired block variant with or without thermal ports: 2-D partial derivative data, 3-D partial derivative data, 4-D partial derivative data
Choose the 3-D flux linkage data | No thermal port or 3-D flux linkage data | Show thermal port variant, and set the Expose neutral port parameter to Yes.

`C` — Motor case
mechanical

Mechanical rotational conserving port associated with the motor case.

`R` — Motor rotor
mechanical

Mechanical rotational conserving port associated with the motor rotor.

`HA` — Winding A thermal port
thermal

Thermal conserving port associated with winding A. For more information, see Thermal Ports.

`HB` — Winding B thermal port
thermal

Thermal conserving port associated with winding B. For more information, see Thermal Ports.

`HC` — Winding C thermal port
thermal

Thermal conserving port associated with winding C. For more information, see Thermal Ports.

`HR` — Rotor thermal port
thermal

Thermal conserving port associated with the rotor. For more information, see Thermal Ports.

Parameters

expand all

Electrical (2-D Partial Derivative Data Variant)

This configuration of the Electrical parameters corresponds to the 2-D Partial Derivative Data block variants, with or without thermal ports. If you are using the 3-D Partial Derivative Data, 4-D Partial Derivative Data, or 3-D Flux Linkage Data variant of the block, see Electrical (3-D Partial Derivative Data Variant), Electrical (4-D Partial Derivative Data Variant), or Electrical (3-D Flux Linkage Data Variant) respectively.

`Parameterization` — Parameterization method
`Assume constant mutual inductance - tabulate with phase current and rotor angle` (default) | `Assume sinusoidal back emf - tabulate with d- and q-axis currents`

Select the parameterization method:

Assume constant mutual inductance - tabulate with phase current and rotor angle — This method assumes that the flux linking each winding depends nonlinearly only on the current in that same winding, plus the rotor angle.
Assume sinusoidal back emf - tabulate with d- and q-axis currents — This method assumes that the flux linking each winding depends nonlinearly on all stator winding currents. It also assumes that the permanent magnet flux linkage is sinusoidal. This option is usually a good fit for interior magnet PMSMs (or IPMSMs).

`Winding type` — Stator windings configuration
`Wye-wound` (default) | `Delta-wound`

Select the configuration for the stator windings:

Wye-wound — The stator windings are wye-wound.
Delta-wound — The stator windings are delta-wound. The a-phase is connected between ports a and b, the b-phase between ports b and c and the c-phase between ports c and a.

`Current vector, i` — Vector of currents
`[-2, 0, 2]` `A` (default)

Vector of currents corresponding to the provided flux linkage partial derivatives. The current vector must be two-sided (have positive and negative values).

Dependencies

This parameter is visible only when you set the Parameterization parameter to Assume constant mutual inductance - tabulate with phase current and rotor angle.

`Rotor angle vector, theta` — Vector of rotor angles
`[0, 20, 40, 60]` `deg` (default)

Vector of rotor angles corresponding to the provided flux linkage partial derivatives. The vector must start at zero. This value corresponds to the angle where the A-phase magnetic flux aligns with the rotor permanent magnetic peak flux direction (the direct-axis, or d-axis). The last value, Θ_max, must be the rotor angle where the flux linkage pattern peaks again. Therefore, the number of pole pairs is 360/Θ_max if Θ_max is expressed in degrees. The default value corresponds to a 6 pole-pair motor.

Dependencies

This parameter is visible only when you set the Parameterization parameter to Assume constant mutual inductance - tabulate with phase current and rotor angle.

`Flux linkage partial derivative wrt current, dPhi(i,theta)/di` — Flux linkage partial derivative with respect to current
`0.0002*ones(3,4)` `Wb/A` (default)

Matrix of the flux linkage partial derivatives with respect to current, defined as a function of current vector and rotor angle vector. Flux linkage is the flux multiplied by the number of winding turns. The default value corresponds to the special case where stator inductance does not depend on stator current or on rotor angle.

Dependencies

This parameter is visible only when you set the Parameterization parameter to Assume constant mutual inductance - tabulate with phase current and rotor angle.

`Flux linkage partial derivative wrt angle, dPhi(i,theta)/dtheta` — Flux linkage partial derivative with respect to angle
`[0, -0.16, 0.16, 0; 0, -0.16, 0.16, 0; 0, -0.16, 0.16, 0]` `Wb/rad` (default)

Matrix of the flux linkage partial derivatives with respect to rotor angle, defined as a function of current vector and rotor angle vector. Flux linkage is the flux multiplied by the number of winding turns. The default value is [0, -0.16, 0.16, 0; 0, -0.16, 0.16, 0; 0, -0.16, 0.16, 0] Wb/rad, which corresponds to the special case where stator inductance does not depend on stator current.

Dependencies

This parameter is visible only when you set the Parameterization parameter to Assume constant mutual inductance - tabulate with phase current and rotor angle.

`Direct axis current vector, id` — Direct axis current vector
`[-200, 0, 200]` `A` (default)

Vector of d-axis currents corresponding to the provided inductances. The current vector must be two-sided (have positive and negative values).