Control Water Level in a Tank Using a DDPG Agent
This example shows how to convert the PI controller in the watertank Simulink® model to a reinforcement learning deep deterministic policy gradient (DDPG) agent. For an example that trains a DDPG agent in MATLAB®, see Compare DDPG Agent to LQR Controller.
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility.
Fix the random number stream with seed zero and random number algorithm Mersenne Twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(0,"twister")previousRngState = struct with fields:
Type: 'twister'
Seed: 0
State: [625×1 uint32]
The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Water Tank Model
The original model for this example is the water tank model. The goal is to control the level of the water in the tank. For more information about the water tank model, see watertank Simulink Model (Simulink Control Design).

Modify the original model by making the following changes:
Delete the PID Controller.
Insert the RL Agent block.
Connect the observation vector , where is the height of the water in the tank, , and is the reference height.
Set up the reward .
Configure the termination signal such that the simulation stops if or .
The resulting model is rlwatertank.slx. For more information on this model and the changes, see Create Custom Simulink Environments.
open_system("rlwatertank")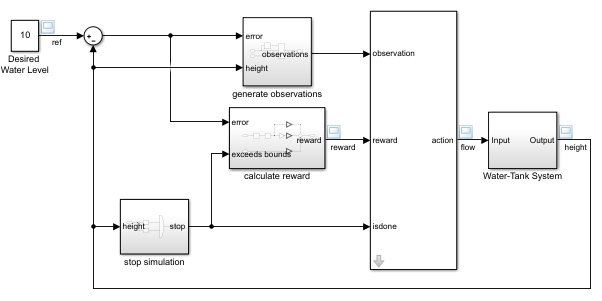
Create the Environment
Creating an environment model includes defining the following:
Action and observation signals that the agent uses to interact with the environment. For more information, see
rlNumericSpecandrlFiniteSetSpec.Reward signal that the agent uses to measure its success. For more information, see Define Observation and Reward Signals in Custom Environments.
Define the observation specification obsInfo and action specification actInfo.
% Observation info obsInfo = rlNumericSpec([3 1],... LowerLimit=[-inf -inf 0 ]',... UpperLimit=[ inf inf inf]'); % Name and description are optional and not used % by the software obsInfo.Name = "observations"; obsInfo.Description = "integrated error, error," + ... " and measured height"; % Action info actInfo = rlNumericSpec([1 1]); actInfo.Name = "flow";
Create the environment object.
env = rlSimulinkEnv("rlwatertank","rlwatertank/RL Agent",... obsInfo,actInfo);
Set a custom reset function that randomizes the reference values for the model. The localResetFcn function is provided at the end of the example.
env.ResetFcn = @localResetFcn;
Specify the agent sample time Ts and the simulation time Tf in seconds.
Ts = 1.0; Tf = 200;
Create the Critic
DDPG agents use a parametrized Q-value function approximator to estimate the value of the policy. A Q-value function critic takes the current observation and an action as inputs and returns a single scalar as output (the estimated discounted cumulative long-term reward for which receives the action from the state corresponding to the current observation, and following the policy thereafter).
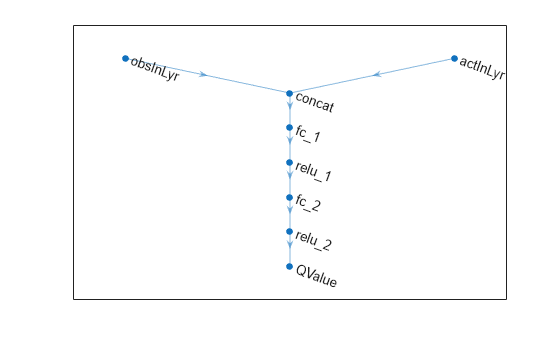
To model the parametrized Q-value function within the critic, use a neural network with two input layers (one for the observation channel, as specified by obsInfo, and the other for the action channel, as specified by actInfo) and one output layer (which returns the scalar value).
Define each network path as an array of layer objects. Assign names to the input and output layers of each path. These names allow you to connect the paths and then later explicitly associate the network input and output layers with the appropriate environment channel. Obtain the dimension of the observation and action spaces from the obsInfo and actInfo specifications.
% Observation path obsPath = featureInputLayer(obsInfo.Dimension(1), ... Name="obsInLyr"); % Action path actPath = featureInputLayer(actInfo.Dimension(1), ... Name="actInLyr"); % Common path commonPath = [ concatenationLayer(1,2,Name="concat") fullyConnectedLayer(25) reluLayer() fullyConnectedLayer(25) reluLayer() fullyConnectedLayer(1,Name="QValue") ]; % Create the network object and add the layers criticNet = dlnetwork(); criticNet = addLayers(criticNet,obsPath); criticNet = addLayers(criticNet,actPath); criticNet = addLayers(criticNet,commonPath); % Connect the layers criticNet = connectLayers(criticNet, ... "obsInLyr","concat/in1"); criticNet = connectLayers(criticNet, ... "actInLyr","concat/in2");
View the critic network configuration.
plot(criticNet)
Initialize the dlnetwork object and summarize its properties. The initial parameters of the critic network are initialized with random values. Fix the random number stream so that the network is always initialized with the same parameter values.
rng(0,"twister");
criticNet = initialize(criticNet);
summary(criticNet) Initialized: true
Number of learnables: 801
Inputs:
1 'obsInLyr' 3 features
2 'actInLyr' 1 features
Create the critic approximator object using the specified deep neural network, the environment specification objects, and the names if the network inputs to be associated with the observation and action channels.
critic = rlQValueFunction(criticNet, ... obsInfo,actInfo, ... ObservationInputNames="obsInLyr", ... ActionInputNames="actInLyr");
For more information on Q-value function objects, see rlQValueFunction.
Check the critic with a random input observation and action.
getValue(critic, ... {rand(obsInfo.Dimension)}, ... {rand(actInfo.Dimension)})
ans = single
-0.4320
For more information on creating critics, see Create Policies and Value Functions.
Create the Actor
DDPG agents use a parametrized deterministic policy over continuous action spaces, which is learned by a continuous deterministic actor.
A continuous deterministic actor implements a parametrized deterministic policy for a continuous action space. This actor takes the current observation as input and returns as output an action that is a deterministic function of the observation.
To model the parametrized policy within the actor, use a neural network with one input layer (which receives the content of the environment observation channel, as specified by obsInfo) and one output layer (which returns the action to the environment action channel, as specified by actInfo).
Define the network as an array of layer objects.
actorNet = [
featureInputLayer(obsInfo.Dimension(1))
fullyConnectedLayer(25)
reluLayer()
fullyConnectedLayer(25)
reluLayer()
fullyConnectedLayer(actInfo.Dimension(1))
];Convert the network to a dlnetwork object and summarize its properties. The initial parameters of the actor network are initialized with random values. Fix the random number stream so that the network is always initialized with the same parameter values.
rng(0,"twister");
actorNet = dlnetwork(actorNet);
summary(actorNet) Initialized: true
Number of learnables: 776
Inputs:
1 'input' 3 features
View the actor network configuration.
plot(actorNet)

Create the actor approximator object using the specified deep neural network, the environment specification objects, and the name if the network input to be associated with the observation channel.
actor = rlContinuousDeterministicActor(actorNet,obsInfo,actInfo);
For more information, see rlContinuousDeterministicActor.
Check the actor with a random input observation.
getAction(actor,{rand(obsInfo.Dimension)})ans = 1×1 cell array
{[-0.1002]}
For more information on creating critics, see Create Policies and Value Functions.
Create the DDPG Agent
Create the DDPG agent using the specified actor and critic approximator objects.
agent = rlDDPGAgent(actor,critic);
For more information, see rlDDPGAgent.
Specify options for the agent, the actor, and the critic using dot notation. For this training:
Use an experience buffer with capcity 1e6 to store experiences. A larger experience buffer can store a diverse set of experiences.
Specify the actor and critic learning rates to be 1e-4 and 1e-3 respectivelky. A large learning rate causes drastic updates which may lead to divergent behaviors, while a low value may require many updates before reaching the optimal point.
Use a gradient threshold of 1 to clip the gradients. Clipping the gradients can improve training stability.
Use mini-batches of 400 experiences. Smaller mini-batches are computationally efficient but may introduce variance in training. By contrast, larger batch sizes can make the training stable but require higher memory.
The discount factor of 1.0 favors long term rewards.
The sample time Ts=1.0 second is assigned to the agent.
agent.AgentOptions.SampleTime = Ts; agent.AgentOptions.DiscountFactor = 1.0; agent.AgentOptions.MiniBatchSize = 400; agent.AgentOptions.ExperienceBufferLength = 1e6; actorOpts = rlOptimizerOptions( ... LearnRate=1e-4, ... GradientThreshold=1); criticOpts = rlOptimizerOptions( ... LearnRate=1e-3, ... GradientThreshold=1); agent.AgentOptions.ActorOptimizerOptions = actorOpts; agent.AgentOptions.CriticOptimizerOptions = criticOpts;
The DDPG agent in this example uses an Ornstein-Uhlenbeck (OU) noise model for exploration. For the noise model:
Specify a standard deviation value of 0.3 to improve exploration during training.
Specify a decay rate of 1e-5 for the standard deviation. The decay causes exploration to reduce gradually as the training progresses.
agent.AgentOptions.NoiseOptions.StandardDeviation = 0.3; agent.AgentOptions.NoiseOptions.StandardDeviationDecayRate = 1e-5;
Alternatively, you can specify the agent options using the rlDDPGAgentOptions object.
Check the agent with a random input observation.
getAction(agent,{rand(obsInfo.Dimension)})ans = 1×1 cell array
{[0.1015]}
Train Agent
To train the agent, first specify the training options. For this example, use the following options:
Run each training for a maximum of 5000 episodes. Specify that each episode lasts for a maximum of
ceil(Tf/Ts)(that is 200) time steps.Display the training progress in the Reinforcement Learning Training Monitor dialog box (set the
Plotsoption) and disable the command line display (set theVerboseoption tofalse).Evaluate the performance of the greedy policy every 10 training episodes, averaging the cumulative reward of 5 simulations.
Stop training when the evaluation score reaches 2000. At this point, the agent can control the level of water in the tank.
For more information on training options, see rlTrainingOptions.
% training options trainOpts = rlTrainingOptions(... MaxEpisodes=5000, ... MaxStepsPerEpisode=ceil(Tf/Ts), ... Plots="training-progress", ... Verbose=false, ... StopTrainingCriteria="EvaluationStatistic", ... StopTrainingValue=2000); % agent evaluator evl = rlEvaluator(EvaluationFrequency=10,NumEpisodes=5);
Fix the random stream for reproducibility.
rng(0,"twister");Train the agent using the train function. Training is a computationally intensive process that takes several minutes to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining =false; if doTraining % Train the agent. trainingStats = train(agent,env,trainOpts,Evaluator=evl); else % Load the pretrained agent for the example. load("WaterTankDDPG.mat","agent") end

Validate Trained Agent
Fix the random stream for reproducibility.
rng(0,"twister");Simulate the agent within the environment, and return the experiences as output.
simOpts = rlSimulationOptions( ... MaxSteps=ceil(Tf/Ts), ... StopOnError="on"); experiences = sim(env,agent,simOpts);
View the performance of the closed loop system using the Scope block in the Simulink model. The agent tracks the reference signal within 5 seconds.

Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
Local Reset Function
function in = localResetFcn(in) % Randomize reference signal blk = sprintf("rlwatertank/Desired \nWater Level"); h = 3*randn + 10; while h <= 0 || h >= 20 h = 3*randn + 10; end in = setBlockParameter(in,blk,Value=num2str(h)); % Randomize initial height h = 3*randn + 10; while h <= 0 || h >= 20 h = 3*randn + 10; end blk = "rlwatertank/Water-Tank System/H"; in = setBlockParameter(in,blk,InitialCondition=num2str(h)); end
See Also
Functions
Objects
rlFiniteSetSpec|rlNumericSpec|rlQValueFunction|rlContinuousDeterministicActor|rlDDPGAgent|rlDDPGAgentOptions|rlTrainingOptions|rlSimulationOptions
Topics
- Compare DDPG Agent to LQR Controller
- Train DQN Agent to Balance Discrete Cart-Pole System
- Train DQN Agent to Swing Up and Balance Pendulum
- Tune PI Controller Using Reinforcement Learning
- Train Reinforcement Learning Agents to Control Quanser QUBE Pendulum
- watertank Simulink Model (Simulink Control Design)
- Water Tank Reinforcement Learning Environment Model
- Reinforcement Learning for Control Systems Applications
- Create Custom Simulink Environments
- Define Observation and Reward Signals in Custom Environments
- Reinforcement Learning Agents
- Train Reinforcement Learning Agents