Imitate MPC Controller for Lane Keeping Assist
This example shows how to train, validate, and test a deep neural network that imitates the behavior of a model predictive controller for an automotive lane keeping assist system. In the example, you also compare the behavior of the deep neural network with that of the original controller.
Model predictive control (MPC) solves a constrained quadratic-programming (QP) optimization problem in real time based on the current state of the plant (for more information, see What Is Model Predictive Control? (Model Predictive Control Toolbox)). Because MPC solves its optimization problem in an open-loop fashion, you can potentially replace the controller with a deep neural network. Evaluating a deep neural network can be more computationally efficient than solving a QP problem in real time.
If the training of the network sufficiently traverses the state-space for the application, you can create a reasonable approximation of the controller behavior. You can then deploy the network for your control application. You can also use the network as a warm starting point for training the actor network of a reinforcement learning agent. For an example, see Train DDPG Agent with Pretrained Actor Network.
Design MPC Controller
Design an MPC controller for lane keeping assist. To do so, first create a dynamic model for the vehicle.
[sys,Vx] = createModelForMPCImLKA;
Create and design the MPC controller object mpcobj. Also, create an mpcstate object for setting the initial controller state. For details on the controller design, type edit createMPCobjImLKA.
[mpcobj,initialState] = createMPCobjImLKA(sys);
For more information on designing model predictive controllers for lane keeping assist applications, see Lane Keeping Assist System Using Model Predictive Control (Model Predictive Control Toolbox) and Lane Keeping Assist with Lane Detection (Automated Driving Toolbox).
Prepare Input Data
The data in InputDataFileImLKA.mat was created by computing the MPC control actions for randomly generated states, previous control actions, and measured disturbances. To generate your own training data, use the collectDataImLKA function, provided in the example folder.
For this example, load the input data from InputDataFileImLKA.mat.
dataStruct = load("InputDataFileImLKA.mat");
data = dataStruct.Data;The columns of the data set are ordered as follows:
Lateral velocity
Yaw angle rate
Lateral deviation
Relative yaw angle
Previous steering angle (control variable)
Measured disturbance (road yaw rate: longitudinal velocity * curvature ())
Cost function value
MPC iterations
Steering angle computed by MPC controller:
Divide the input data into training, validation, and testing data. First, determine the number of validation data rows based on a given percentage.
totalRows = size(data,1); validationSplitPercent = 0.1; numValidationDataRows = floor(validationSplitPercent*totalRows);
Determine the number of test data rows based on a given percentage.
testSplitPercent = 0.05; numTestDataRows = floor(testSplitPercent*totalRows);
Randomly extract validation and testing data from the input data set. To do so, first randomly extract enough rows for both data sets.
randomIdx = randperm(totalRows,numValidationDataRows+numTestDataRows); randomData = data(randomIdx,:);
Divide the random data into validation and testing data.
validationData = randomData(1:numValidationDataRows,:); testData = randomData(numValidationDataRows + 1:end,:);
Extract the remaining rows as training data.
trainDataIdx = setdiff(1:totalRows,randomIdx); trainData = data(trainDataIdx,:);
Randomize the training data.
numTrainDataRows = size(trainData,1); shuffleIdx = randperm(numTrainDataRows); shuffledTrainData = trainData(shuffleIdx,:);
Reshape the training and validation data into 4-D matrices for use with trainNetwork.
numObs = 6;
numActions = 1;
trainInput = shuffledTrainData(:,1:6);
trainOutput = shuffledTrainData(:,9);
validationInput = validationData(:,1:6);
validationOutput = validationData(:,9);
validationCellArray = {validationInput,validationOutput};Reshape the testing data for use with predict.
testDataInput = testData(:,1:6); testDataOutput = testData(:,9);
Create Deep Neural Network
The deep neural network architecture uses the following layers.
imageInputLayeris the input layer of the neural network.fullyConnectedLayermultiplies the input by a weight matrix and then adds a bias vector.reluLayeris the activation function of the neural network.tanhLayerconstrains the value to the range to [-1,1].scalingLayerscales the value to the range to [-1.04,1.04], this constrains the steering angle to the range [-60,60].
Fix the random seed for reproducibility.
rng(0);
Create the deep neural network that will imitate the MPC controller after training.
imitateMPCLayers = [
featureInputLayer(numObs)
fullyConnectedLayer(45)
reluLayer
fullyConnectedLayer(45)
reluLayer
fullyConnectedLayer(45)
reluLayer
fullyConnectedLayer(numActions)
tanhLayer
scalingLayer(Scale=1.04)
];Plot the network.
plot(dlnetwork(imitateMPCLayers))

Train Deep Neural Network
Specify training options.
options = trainingOptions("adam", ... Verbose=false, ... Plots="training-progress", ... Metrics="rmse", ... Shuffle="every-epoch", ... MaxEpochs=30, ... MiniBatchSize=512, ... ValidationData=validationCellArray, ... InitialLearnRate=1e-3, ... GradientThresholdMethod="absolute-value", ... ExecutionEnvironment="cpu", ... GradientThreshold=10, ... Epsilon=1e-8);
Train the deep neural network. To view detailed training information in the Command Window, set the Verbose training option to true.
imitateMPCNetwork = trainnet( ... trainInput, ... trainOutput, ... imitateMPCLayers, ... "mse", ... options);
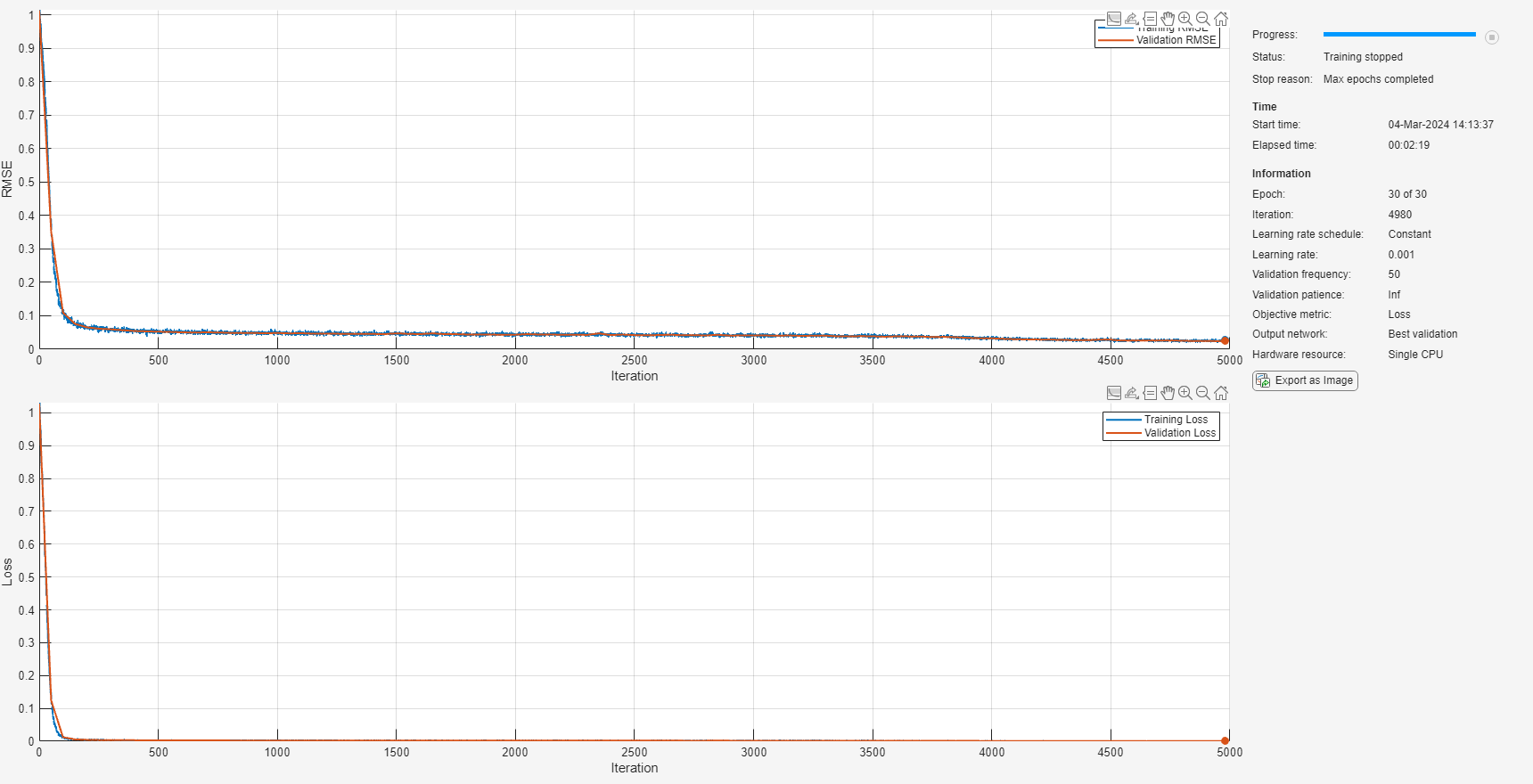
Training of the deep neural network stops after the final iteration.
The training and validation loss are nearly the same for each mini-batch, which indicates that the trained network does not overfit.
Test Trained Network
Check that the trained deep neural network returns steering angles similar to the MPC controller control actions given the test input data. Compute the network output using the predict function.
predictedTestDataOutput = predict(imitateMPCNetwork,testDataInput);
Calculate the root mean squared error (RMSE) between the network output and the testing data.
testRMSE = sqrt(mean((testDataOutput - predictedTestDataOutput).^2));
fprintf("Test Data RMSE = %d\n", testRMSE);Test Data RMSE = 2.468181e-02
The small RMSE value indicates that the network outputs closely reproduce the MPC controller outputs.
Compare Trained Network with MPC Controller
To compare the performance of the MPC controller and the trained deep neural network, run closed-loop simulations using the vehicle plant model.
Generate random initial conditions for the vehicle that are not part of the original input data set, with values selected from the following ranges:
Lateral velocity — Range (-2,2) m/s
Yaw angle rate — Range (-1.04,1.04) rad/s
Lateral deviation — Range (-1,1) m
Relative yaw angle — Range (-0.8,0.8) rad
Last steering angle (control variable) — Range (-1.04,1.04) rad
Measured disturbance (road yaw rate, defined as longitudinal velocity * curvature ()) — Range (-0.01,0.01) with a minimum road radius of 100 m
rng(5e7) [x0,u0,rho] = generateRandomDataImLKA(data);
Set the initial plant state and control action in the mpcstate object.
initialState.Plant = x0; initialState.LastMove = u0;
Extract the sample time from the MPC controller. Also, set the number of simulation steps.
Ts = mpcobj.Ts; Tsteps = 30;
Obtain the A and B state-space matrices for the vehicle model.
A = sys.A; B = sys.B;
Initialize the state and input trajectories for the MPC controller simulation.
xHistoryMPC = repmat(x0',Tsteps+1,1); uHistoryMPC = repmat(u0',Tsteps,1);
Run a closed-loop simulation of the MPC controller and the plant using the mpcmove function.
for k = 1:Tsteps % Obtain plant outputs xk = xHistoryMPC(k,:)'; % Compute control action using the MPC controller uk = mpcmove(mpcobj,initialState,xk,zeros(1,4),Vx*rho); % Store the control action uHistoryMPC(k,:) = uk; % Update plant state using the control action xHistoryMPC(k+1,:) = (A*xk + B*[uk;Vx*rho])'; end
Initialize the state and input trajectories for the deep neural network simulation.
xHistoryDNN = repmat(x0',Tsteps+1,1); uHistoryDNN = repmat(u0',Tsteps,1); lastMV = u0;
Run a closed-loop simulation of the trained network and the plant. The neuralnetLKAmove function, provided in the example folder, computes the deep neural network output using the predict function.
for k = 1:Tsteps % Obtain plant outputs xk = xHistoryDNN(k,:)'; % Predict the next move using trained network uk = neuralnetLKAmove(imitateMPCNetwork,xk,lastMV,rho); % Store control action uHistoryDNN(k,:) = uk; % Update the last MV for the next step lastMV = uk; % Update plant state using the control action xHistoryDNN(k+1,:) = (A*xk + B*[uk;Vx*rho])'; end
Plot the results to compare the MPC controller and trained deep neural network (DNN) trajectories.
plotValidationResultsImLKA(Ts, ... xHistoryDNN,uHistoryDNN, ... xHistoryMPC,uHistoryMPC);
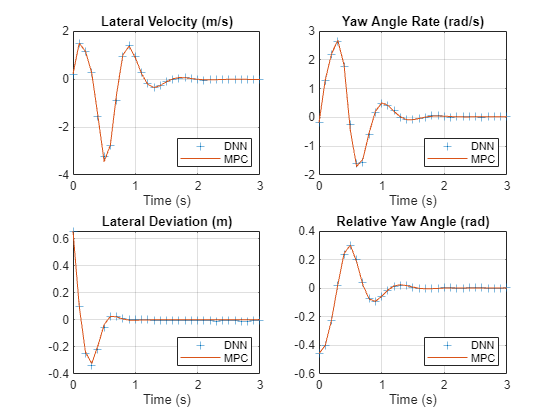
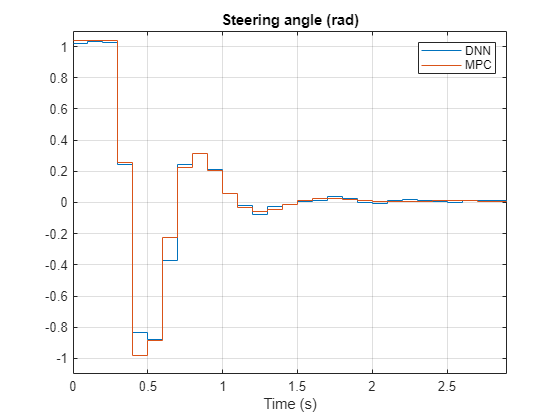
The deep neural network successfully imitates the behavior of the MPC controller. The vehicle state and control action trajectories for the controller and the deep neural network closely align.
See Also
Functions
trainNetwork|predict|mpcmove(Model Predictive Control Toolbox)
Objects
SeriesNetwork|mpc(Model Predictive Control Toolbox)
Topics
- Train DDPG Agent with Pretrained Actor Network
- Lane Keeping Assist System Using Model Predictive Control (Model Predictive Control Toolbox)
- Lane Keeping Assist with Lane Detection (Automated Driving Toolbox)
- What Is Model Predictive Control? (Model Predictive Control Toolbox)