rfckt.parallelplate
Parallel-plate transmission line
Description
Use the rfckt.parallelplate object to create a
parallel-plate transmission line that is characterized by line dimensions and optional
stub properties.
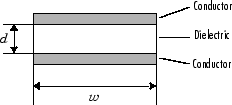
A parallel-plate transmission line is shown in cross-section in the following figure. Its physical characteristics include the plate width w and the plate separation d.
Note
txlineParallelPlate is recommended over
rfckt.parallelplate because it enables you to:
Create a parallel-plate transmission line.
Build a
circuitobject with a parallel-plate transmission line.Model a parallel-plate transmission line element in an RF chain created using an
rfbudgetobject or the RF Budget Analyzer app, and then export this element to RF Blockset™ or torfsystemSystem object™ for circuit envelope analysis.
(since R2023b)
Creation
Description
h = rfckt.parallelplate returns a parallel-plate
transmission line object whose properties are set to their default
values.
h = rfckt.parallelplate(Name,Value) sets properties
using one or more name-value pairs. For example,
rfckt.parallelplate('LineLength',0.045) creates a
parallel-plate transmission line object with a physical length of 0.045
meters. You can specify multiple name-value pairs. Enclose each property
name in a quote. Properties not specified retain their default
values.
Properties
Object Functions
analyze | Analyze RFCKT object in frequency domain |
calculate | Calculate specified parameters for rfckt objects or rfdata objects |
circle | Draw circles on Smith Chart |
extract | Extract specified network parameters from rfckt object or data object |
listformat | List valid formats for specified circuit object parameter |
listparam | List valid parameters for specified circuit object |
loglog | Plot specified circuit object parameters using log-log scale |
plot | Plot circuit object parameters on X-Y plane |
plotyy | Plot parameters of RF circuit or RF data on xy-plane with two Y-axes |
getop | Display operating conditions |
polar | Plot specified object parameters on polar coordinates |
semilogx | Plot RF circuit object parameters using log scale for x-axis |
semilogy | Plot RF circuit object parameters using log scale for y-axis |
smith | Plot circuit object parameters on Smith Chart |
write | Write RF data from circuit or data object to file |
getz0 | Calculate characteristic impedance of RFCKT transmission line object |
read | Read RF data from file to new or existing circuit or data object |
restore | Restore data to original frequencies |
getop | Display operating conditions |
groupdelay | Group delay of S-parameter object or RF filter object or RF Toolbox circuit object |
Examples
Algorithms
The analyze method treats the parallel-plate line as a 2-port
linear network and models the line as a transmission line with optional stubs. The
analyze method computes the AnalyzedResult
property of the line using the data stored in the rfckt.parallelplate
object properties as follows:
If you model the transmission line as a stub less line, the
analyzemethod first calculates the ABCD-parameters at each frequency contained in the modeling frequencies vector. It then uses theabcd2sfunction to convert the ABCD-parameters to S-parameters.The
analyzemethod calculates the ABCD-parameters using the physical length of the transmission line, d, and the complex propagation constant, k, using the following equations:Z0 and k are vectors whose elements correspond to the elements of f, the vector of frequencies specified in the
analyzeinput argumentfreq. Both can be expressed in terms of the resistance (R), inductance (L), conductance (G), and capacitance (C) per unit length (meters) as follows:where
In these equations:
w is the plate width.
d is the plate separation.
σcond is the conductivity in the conductor.
μ is the permeability of the dielectric.
ε is the permittivity of the dielectric.
ε″ is the imaginary part of ε, ε″ = ε0εrtan δ, where:
ε0 is the permittivity of free space.
εr is the
EpsilonRproperty value.tan δ is the
LossTangentproperty value.
δcond is the skin depth of the conductor, which the block calculates as .
f is a vector of modeling frequencies determined by the Outport (RF Blockset) block.
If you model the transmission line as a shunt or series stub, the
analyzemethod first calculates the ABCD-parameters at the specified frequencies. It then uses theabcd2sfunction to convert the ABCD-parameters to S-parameters.When you set the
StubModeproperty to'Shunt', the 2-port network consists of a stub transmission line that you can terminate with either a short circuit or an open circuit as shown in the following figure.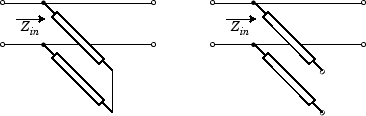
Zin is the input impedance of the shunt circuit. The ABCD-parameters for the shunt stub are calculated as:
When you set the
StubModeproperty to'Series', the 2-port network consists of a series transmission line that you can terminate with either a short circuit or an open circuit as shown in the following figure.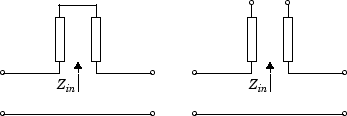
Zin is the input impedance of the series circuit. The ABCD-parameters for the series stub are calculated as:
References
[1] Pozar, David M. Microwave Engineering, John Wiley & Sons, Inc., 2005.
Version History
Introduced in R2009a
See Also
rfckt.amplifier | rfckt.cascade | rfckt.coaxial | rfckt.cpw | rfckt.datafile | rfckt.delay | rfckt.hybrid | rfckt.hybridg | rfckt.mixer | rfckt.microstrip | rfckt.passive | rfckt.parallel | rfckt.rlcgline | rfckt.series | rfckt.seriesrlc | rfckt.shuntrlc | rfckt.twowire | rfckt.txline
