freqs

Frequency response of analog filters

Syntax

h = freqs(b,a,w)

[h,wout] = freqs(b,a,n)

freqs(___)

Description

h = freqs(b,a,w) returns the complex frequency response of the analog filter specified by the coefficient vectors b and a, evaluated at the angular frequencies w.

[h,wout] = freqs(b,a,n) uses n frequency points to compute h and returns the corresponding angular frequencies in wout.

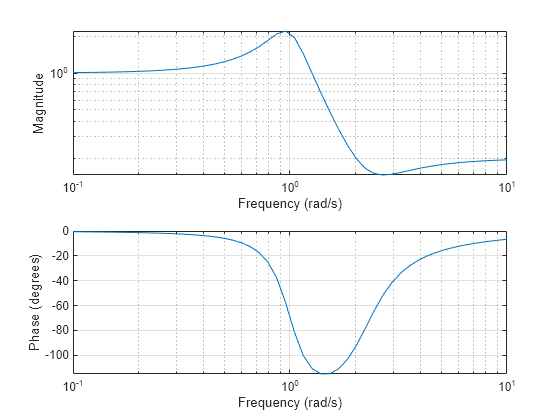
freqs(___) with no output arguments plots the magnitude and phase responses as functions of angular frequency in the current figure window. You can use this syntax with either of the previous input syntaxes.

Examples

Frequency Response from Transfer Function

Find and graph the frequency response of the transfer function

$$H(s)=\frac{0.2s^2+0.3s+1}{s^2+0.4s+1}.$$

a = [1 0.4 1];
b = [0.2 0.3 1];
w = logspace(-1,1);

h = freqs(b,a,w);
mag = abs(h);
phase = angle(h);
phasedeg = phase*180/pi;

subplot(2,1,1)
loglog(w,mag)
grid on
xlabel('Frequency (rad/s)')
ylabel('Magnitude')

subplot(2,1,2)
semilogx(w,phasedeg)
grid on
xlabel('Frequency (rad/s)')
ylabel('Phase (degrees)')

You can also generate the plots by calling freqs with no output arguments.

figure
freqs(b,a,w)

Comparison of Analog IIR Lowpass Filters

Design a fifth-order analog Butterworth lowpass filter with a cutoff frequency of 2 GHz. Multiply by $$2\pi$$ to convert the frequency to radians per second. Compute the frequency response of the filter at 4096 points.

n = 5;
wn = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';

[zb,pb,kb] = butter(n,wn,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);

Design a fifth-order Chebyshev Type I filter with a passband edge frequency of 2 GHz and 3 dB of passband ripple. Compute its frequency response.

wp = wn;

[z1,p1,k1] = cheby1(n,3,wp,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);

Design a fifth-order Chebyshev Type II filter with a stopband edge frequency of 2.5 GHz and 30 dB of stopband attenuation. Compute its frequency response.

ws = 2*pi*2.5e9;

[z2,p2,k2] = cheby2(n,30,ws,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);

Design a fifth-order elliptic filter with the same passband and stopband edge frequencies, 3 dB of passband ripple, and 30 dB of stopband attenuation. Compute its frequency response.

[ze,pe,ke] = ellip(n,3,30,wp,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);

Design a fifth-order Bessel filter with the same edge frequency. Compute its frequency response.

[zf,pf,kf] = besself(n,wn);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,w);
gdf = -diff(unwrap(angle(hf)))./diff(wf);

Plot the attenuation in decibels. Express the frequency in gigahertz. Compare the filters.

fGHz = [wb w1 w2 we wf]/(2e9*pi);
plot(fGHz,mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid on
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"], ...
    Location="southwest")

The Butterworth and Chebyshev Type II filters have flat passbands and wide transition bands. The Chebyshev Type I and elliptic filters roll off faster but have passband ripple. The frequency input to the Chebyshev Type II design function sets the beginning of the stopband rather than the end of the passband. Elliptic filters offer steeper rolloff characteristics than Butterworth and Chebyshev filters, but they are equiripple in both the passband and the stopband. Of these four classical filter types, elliptic filters usually meet a given set of filter performance specifications with the lowest filter order.

Plot the group delay in samples. Express the frequency in gigahertz and the group delay in nanoseconds. Compare the filters. The Bessel filter has approximately constant group delay along the passband.

gdns = [gdb gd1 gd2 gde gdf]*1e9;
gdns(gdns<0) = NaN;
loglog(fGHz(2:end,:),gdns)
grid on
xlabel("Frequency (GHz)")
ylabel("Group delay (ns)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"], ...
    Location="southwest")

Frequency Response of a Lowpass Analog Bessel Filter

Design a 5th-order analog lowpass Bessel filter with an approximately constant group delay up to $$10^4$$ rad/s. Plot the frequency response of the filter using freqs.

[b,a] = besself(5,10000);   % Bessel analog filter design
freqs(b,a)                  % Plot frequency response

Input Arguments

b, a — Transfer function coefficients

vectors

Transfer function coefficients, specified as vectors. b contains the numerator coefficients and a contains the denominator coefficients.

Example: [b,a] = butter(5,50,'s') specifies a fifth-order Butterworth filter with a cutoff frequency of 50 rad/second.

Data Types: single | double

w — Angular frequencies

positive real vector

Angular frequencies, specified as a positive real vector expressed in rad/second.

Example: 2*pi*logspace(6,9) specifies 50 logarithmically spaced angular frequencies from 1 MHz (2π × 10⁶ rad/second) and 1 GHz (2π × 10⁹ rad/second).

Data Types: single | double

n — Number of evaluation points

200 (default) | positive integer scalar

Number of evaluation points, specified as a positive integer scalar.

Data Types: single | double

Output Arguments

h — Frequency response

vector

Frequency response, returned as a vector.

wout — Angular frequencies

vector

Angular frequencies at which h is computed, returned as a vector.

Algorithms

freqs returns the complex frequency response of an analog filter specified by b and a. The function evaluates the ratio of Laplace transform polynomials

$$H(s)=\frac{B(s)}{A(s)}=\frac{b(1)s^n+b(2)s^{n-1}+\cdots +b(n+1)}{a(1)s^m+a(2)s^{m-1}+\cdots +a(m+1)}$$

along the imaginary axis at the frequency points s = jω:

s = 1j*w;
h = polyval(b,s)./polyval(a,s);

Version History

Introduced before R2006a