stft
Short-time Fourier transform
Syntax
Description
s = stft(x)x.
s = stft(___,Name=Value)
stft(___) with no output arguments plots the
magnitude squared of the STFT in decibels in the current figure window.
Examples
Generate a chirp with sinusoidally varying frequency. The signal is sampled at 10 kHz for two seconds.
fs = 10e3; t = 0:1/fs:2; x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);
Compute the short-time Fourier transform of the chirp. Divide the signal into 256-sample segments and window each segment using a Kaiser window with shape parameter β = 5. Specify 220 samples of overlap between adjoining segments and a DFT length of 512. Output the frequency and time values at which the STFT is computed.
[s,f,t] = stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512);
The magnitude squared of the STFT is also known as the spectrogram. Plot the spectrogram in decibels. Specify a colormap that spans 60 dB and whose last color corresponds to the maximum value of the spectrogram.
sdb = mag2db(abs(s)); mesh(t,f/1000,sdb); cc = max(sdb(:))+[-60 0]; ax = gca; ax.CLim = cc; view(2) colorbar
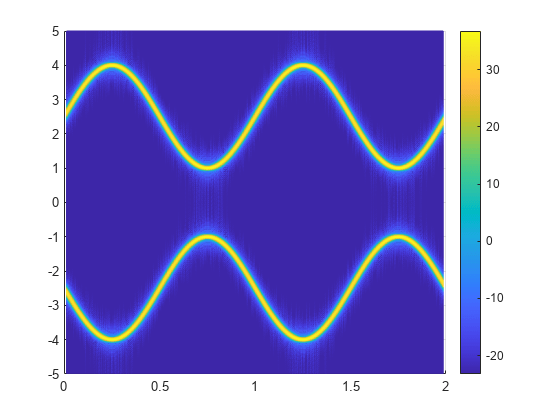
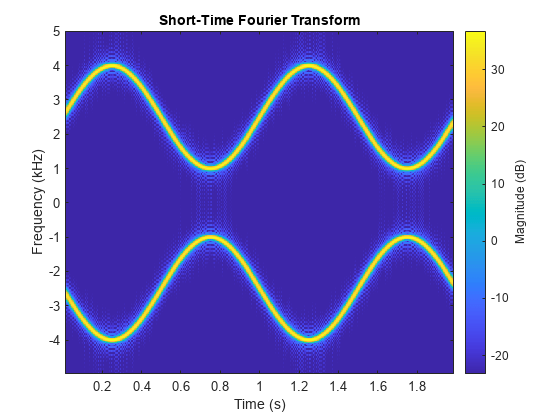
Obtain the same plot by calling the stft function with no output arguments.
stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512)
Generate a quadratic chirp sampled at 1 kHz for 2 seconds. The instantaneous frequency is 100 Hz at and crosses 200 Hz at second.
ts = 0:1/1e3:2; f0 = 100; f1 = 200; x = chirp(ts,f0,1,f1,"quadratic",[],"concave");
Compute and display the STFT of the quadratic chirp with a duration of 1 ms.
d = seconds(1e-3);
win = hamming(100,"periodic");
stft(x,d,Window=win,OverlapLength=98,FFTLength=128);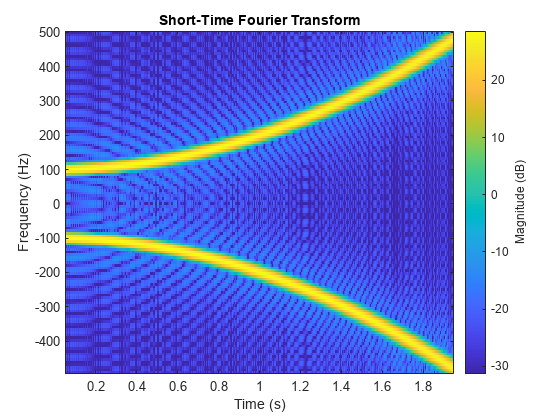
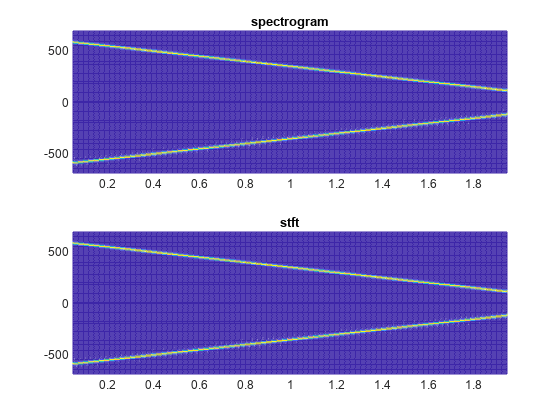
Generate a signal consisting of a chirp sampled at 1.4 kHz for 2 seconds. The frequency of the chirp decreases linearly from 600 Hz to 100 Hz during the measurement time.
fs = 1400; x = chirp(0:1/fs:2,600,2,100);
stft Defaults
Compute the STFT of the signal using the spectrogram and stft functions. Use the default values of the stft function:
Divide the signal into 128-sample segments and window each segment with a periodic Hann window.
Specify 96 samples of overlap between adjoining segments. This length is equivalent to 75% of the window length.
Specify 128 DFT points and center the STFT at zero frequency, with the frequency expressed in hertz.
Verify that the two results are equal.
M = 128; g = hann(M,"periodic"); L = 0.75*M; Ndft = 128; [sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered"); [s,f,t] = stft(x,fs); dff = max(max(abs(sp-s)))
dff = 0
Use the mesh function to plot the two outputs.
nexttile mesh(tp,fp,abs(sp).^2) title("spectrogram") view(2), axis tight nexttile mesh(t,f,abs(s).^2) title("stft") view(2), axis tight
spectrogram Defaults
Repeat the computation using the default values of the spectrogram function:
Divide the signal into segments of length , where is the length of the signal. Window each segment with a Hamming window.
Specify 50% overlap between segments.
To compute the FFT, use points. Compute the spectrogram only for positive normalized frequencies.
M = floor(length(x)/4.5); g = hamming(M); L = floor(M/2); Ndft = max(256,2^nextpow2(M)); [sx,fx,tx] = spectrogram(x); [st,ft,tt] = stft(x,Window=g,OverlapLength=L, ... FFTLength=Ndft,FrequencyRange="onesided"); dff = max(max(sx-st))
dff = 0
Use the waterplot function to plot the two outputs. Divide the frequency axis by in both cases. For the stft output, divide the sample numbers by the effective sample rate, .
figure nexttile waterplot(sx,fx/pi,tx) title("spectrogram") nexttile waterplot(st,ft/pi,tt/(2*pi)) title("stft")
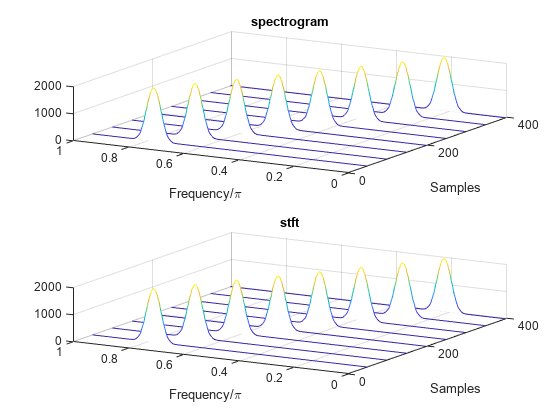
function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency/\pi") ylabel("Samples") end
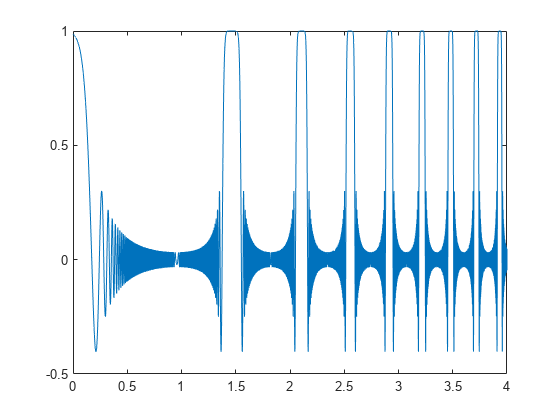
Generate a signal sampled at 5 kHz for 4 seconds. The signal consists of a set of pulses of decreasing duration separated by regions of oscillating amplitude and fluctuating frequency with an increasing trend. Plot the signal.
fs = 5000; t = 0:1/fs:4-1/fs; x = besselj(0,600*(sin(2*pi*(t+1).^3/30).^5)); plot(t,x)
Compute the one-sided, two-sided, and centered short-time Fourier transforms of the signal. In all cases, use a 202-sample Kaiser window with shape factor to window the signal segments. Display the frequency range used to compute each transform.
rngs = ["onesided" "twosided" "centered"]; for kj = 1:length(rngs) opts = {'Window',kaiser(202,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end
![Figure contains 3 axes objects. Axes object 1 with title 'onesided': [0.000, 2.500] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title 'twosided': [0.000, 4.975] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 3 with title 'centered': [-2.475, 2.500] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.](../../examples/signal/win64/STFTFrequencyRangesExample_02.png)
Repeat the computation, but now change the length of the Kaiser window to 203, an odd number. The 'twosided' frequency interval does not change. The other two frequency intervals become open at the higher end.
for kj = 1:length(rngs) opts = {'Window',kaiser(203,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end
![Figure contains 3 axes objects. Axes object 1 with title 'onesided': [0.000, 2.488] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title 'twosided': [0.000, 4.975] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 3 with title 'centered': [-2.488, 2.488] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.](../../examples/signal/win64/STFTFrequencyRangesExample_03.png)
Generate a three-channel signal consisting of three different chirps sampled at 1 kHz for one second.
The first channel consists of a concave quadratic chirp with instantaneous frequency 100 Hz at t = 0 and crosses 300 Hz at t = 1 second. It has an initial phase equal to 45 degrees.
The second channel consists of a convex quadratic chirp with instantaneous frequency 100 Hz at t = 0 and crosses 500 Hz at t = 1 second.
The third channel consists of a logarithmic chirp with instantaneous frequency 300 Hz at t = 0 and crosses 500 Hz at t = 1 second.
Compute the STFT of the multichannel signal using a periodic Hamming window of length 128 and an overlap length of 50 samples.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,'quadratic',45,'concave'); chirp(t,100,1,500,'quadratic',[],'convex'); chirp(t,300,1,500,'logarithmic')]'; [S,F,T] = stft(x,fs,'Window',hamming(128,'periodic'),'OverlapLength',50);
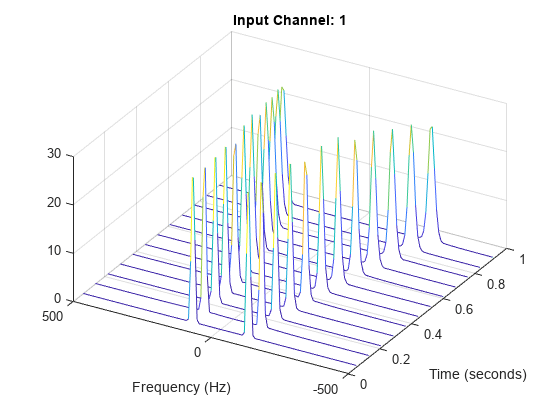
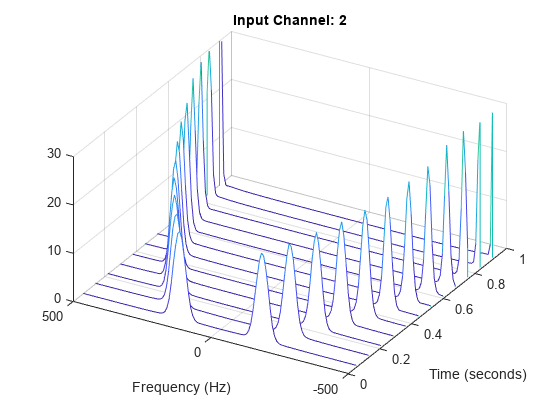
Visualize the STFT of each channel as a waterfall plot. Control the behavior of the axes using the helper function helperGraphicsOpt.
waterfall(F,T,abs(S(:,:,1))') helperGraphicsOpt(1)
waterfall(F,T,abs(S(:,:,2))') helperGraphicsOpt(2)
waterfall(F,T,abs(S(:,:,3))') helperGraphicsOpt(3)
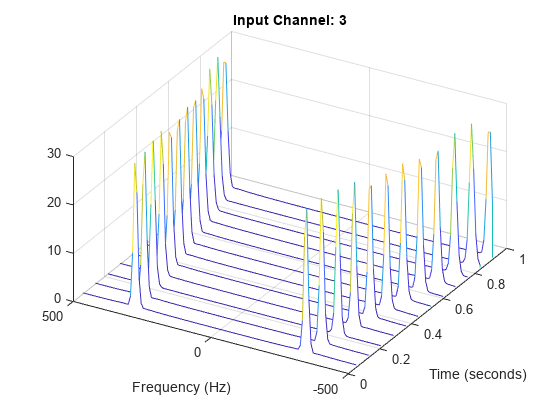
This helper function sets the appearance and behavior of the current axes.
function helperGraphicsOpt(ChannelId) ax = gca; ax.XDir = 'reverse'; ax.ZLim = [0 30]; ax.Title.String = ['Input Channel: ' num2str(ChannelId)]; ax.XLabel.String = 'Frequency (Hz)'; ax.YLabel.String = 'Time (seconds)'; ax.View = [30 45]; end
Input Arguments
Input signal, specified as a vector, a matrix, or a MATLAB®
timetable.
Note
If you want x and s to be the same
length, the value of
(length(
must be an integer. Use x)-noverlap)/(length(window)-noverlap)Window
to specify the length of window and OverlapLength to specify noverlap.
If the input has multiple channels, specify
xas a matrix where each column corresponds to a channel.For timetable input,
xmust contain uniformly increasing finite row times. If a timetable has missing or duplicate time points, you can fix it using the tips in Clean Timetable with Missing, Duplicate, or Nonuniform Times.For multichannel timetable input, specify
xas a timetable with a single variable containing a matrix or a timetable with multiple variables each containing a column vector. All variables must have the same precision.
Each channel of x must have a length greater than or
equal to the window length.
Example: chirp(0:1/4e3:2,250,1,500,"quadratic") specifies a
single-channel chirp.
Example: timetable(rand(5,2),SampleRate=1) specifies a two-channel
random variable sampled at 1 Hz for 4 seconds.
Example: timetable(rand(5,1),rand(5,1),SampleRate=1) specifies a
two-channel random variable sampled at 1 Hz for 4 seconds.
Data Types: double | single
Complex Number Support: Yes
Sample rate, specified as a positive scalar. This argument applies only when
x is a vector or a matrix.
Data Types: double | single
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Window=hamming(100),OverlapLength=50,FFTLength=128 windows
the data using a 100-sample Hamming window, with 50 samples of overlap between adjoining
segments and a 128-point FFT.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Window',hamming(100),'OverlapLength',50,'FFTLength',128
windows the data using a 100-sample Hamming window, with 50 samples of overlap between
adjoining segments and a 128-point FFT.
Spectral window, specified as a vector. If you do not specify the window or
specify it as empty, the function uses a Hann window of length 128. The length of
Window must be greater than or equal to 2.
For a list of available windows, see Windows.
Example: hann(N+1) and
(1-cos(2*pi*(0:N)'/N))/2 both specify a Hann window of length
N + 1.
Data Types: double | single
Number of overlapped samples, specified as a positive integer smaller than the
length of Window. If you omit OverlapLength
or specify it as empty, it is set to the largest integer less than 75% of the window
length, which is 96 samples for the default Hann window.
Data Types: double | single
Number of DFT points, specified as a positive integer. The value must be greater than or equal to the window length. If the length of the input signal is less than the DFT length, the data is padded with zeros.
Data Types: double | single
STFT frequency range, specified as "centered",
"twosided", or "onesided".
"centered"— Compute a two-sided, centered STFT. IfFFTLengthis even, thensis computed over the interval (–π, π] rad/sample. IfFFTLengthis odd, thensis computed over the interval (–π, π) rad/sample. If you specify time information, then the intervals are (–fs, fs/2] cycles/unit time and (–fs, fs/2) cycles/unit time, respectively, where fs is the effective sample rate."twosided"— Compute a two-sided STFT over the interval [0, 2π) rad/sample. If you specify time information, then the interval is [0, fs) cycles/unit time."onesided"— Compute a one-sided STFT. IfFFTLengthis even, thensis computed over the interval [0, π] rad/sample. IfFFTLengthis odd, thensis computed over the interval [0, π) rad/sample. If you specify time information, then the intervals are [0, fs/2] cycles/unit time and [0, fs/2) cycles/unit time, respectively, where fs is the effective sample rate. This option is valid only for real signals.Note
When this argument is set to
"onesided",stftoutputs the values in the positive Nyquist range and does not conserve the total power.
For an example, see STFT Frequency Ranges.
Data Types: char | string
Output time dimension, specified as "acrosscolumns" or
"downrows". Set this value to "downrows" if
you want the time dimension of s down the rows and the frequency
dimension across the columns. Set this value to "acrosscolumns" if
you want the time dimension of s across the columns and the
frequency dimension down the rows. This input is ignored if the function is called
without output arguments.
Output Arguments
Short-time Fourier transform, returned as a matrix or a 3-D array. Time increases
across the columns of s and frequency increases down the rows. The
third dimension, if present, corresponds to the input channels.
If the signal
xhas Nx time samples, thenshas k columns, where k = ⌊(Nx–L)/(M–L)⌋, M is the length ofWindow, L is theOverlapLength, and the ⌊ ⌋ symbols denote the floor function.The number of rows in
sis equal to the value specified inFFTLength.
Data Types: double | single
Frequencies at which the STFT is evaluated, returned as a vector.
Data Types: double | single
Time instants, returned as a vector. t contains the time values
corresponding to the centers of the data segments used to compute short-time power
spectrum estimates.
Data Types: double | single
More About
The short-time Fourier transform (STFT) is used to analyze how the frequency content of a nonstationary signal changes over time. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal. For more information about the spectrogram and how to compute it using Signal Processing Toolbox™ functions, see Spectrogram Computation with Signal Processing Toolbox.
The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has
columns, where Nx is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals NDFT, the number of DFT points, for centered and two-sided transforms and an odd number close to NDFT/2 for one-sided transforms of real-valued signals.
The mth column of the STFT matrix contains the DFT of the windowed data centered about time mR:
References
[1] Mitra, Sanjit K. Digital Signal Processing: A Computer-Based Approach. 2nd Ed. New York: McGraw-Hill, 2001.
[2] Sharpe, Bruce. Invertibility of Overlap-Add Processing. https://gauss256.github.io/blog/cola.html, accessed July 2019.
[3] Smith, Julius Orion. Spectral Audio Signal Processing. https://ccrma.stanford.edu/~jos/sasp/, online book, 2011 edition, accessed Nov 2018.
Extended Capabilities
The
stft function supports tall arrays with the following usage
notes and limitations:
OutputTimeDimension must always be specified and set to
"downrows".
For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Timetables are not supported for code generation.
Usage notes and limitations:
The syntax with no output arguments is not supported.
For more information, see Run MATLAB Functions in Thread-Based Environment.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2019a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)