Chirp Z-Transform
The chirp Z-transform (CZT) is useful in evaluating the Z-transform along contours other than the unit circle. The chirp Z-transform is also more efficient than the DFT algorithm for the computation of prime-length transforms, and it is useful in computing a subset of the DFT for a sequence. The chirp Z-transform, or CZT, computes the Z-transform along spiral contours in the z-plane for an input sequence. Unlike the DFT, the CZT is not constrained to operate along the unit circle, but can evaluate the Z-transform along contours described by , where A is the complex starting point, W is a complex scalar describing the complex ratio between points on the contour, and M is the length of the transform.
One possible spiral is
a = 0.8*exp(1j*pi/6); w = 0.995*exp(-1j*pi*.05); m = 91; z = a*(w.^(-(0:m-1)')); zplane(z)
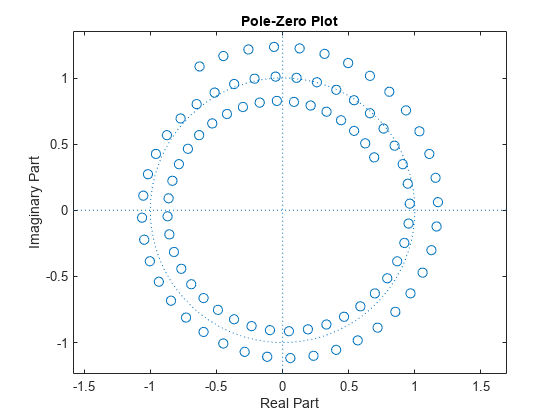
czt(x,m,w,a) computes the Z-transform of x on these points.
An interesting and useful spiral set is m evenly spaced samples around the unit circle, parameterized by and . The Z-transform on this contour is simply the DFT, obtained by czt:
M = 64; m = 0:M-1; x = sin(2*pi*m/15); FFT = fft(x); CZT = czt(x,M,exp(-2j*pi/M),1); stem(m,abs(FFT)) hold on stem(m,abs(CZT),'*') hold off legend('fft','czt','Location','north')
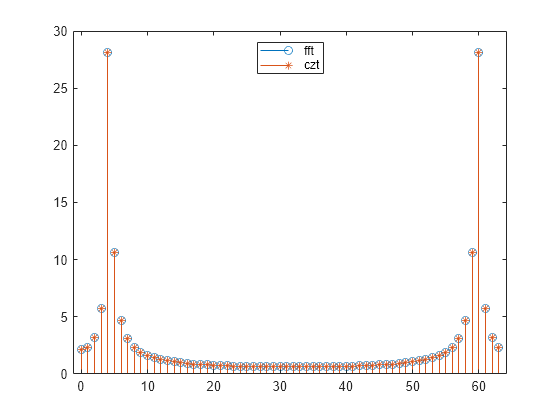
czt may be faster than the fft function for computing the DFT of sequences with certain odd lengths, particularly long prime-length sequences.