Formant Estimation with LPC Coefficients
This example shows how to estimate vowel formant frequencies using linear predictive coding (LPC). The formant frequencies are obtained by finding the roots of the prediction polynomial.
This example uses the speech sample mtlb.mat, which is part of Signal Processing Toolbox™. The speech is lowpass-filtered. Because of the low sampling frequency, this speech sample is not optimal for this example. The low sampling frequency limits the order of the autoregressive model you can fit to the data. In spite of this limitation, the example illustrates the technique for using LPC coefficients to determine vowel formants.
Load the speech signal. The recording is a woman saying "MATLAB®". The sampling frequency is 7418 Hz.
load mtlbThe MAT file contains the speech waveform, mtlb, and the sampling frequency, Fs.
Use the spectrogram function to identify a voiced segment for analysis.
segmentlen = 100; noverlap = 90; NFFT = 128; spectrogram(mtlb,segmentlen,noverlap,NFFT,Fs,'yaxis') title('Signal Spectrogram')
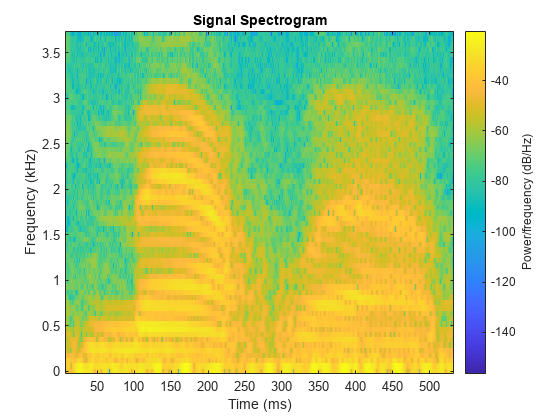
Extract the segment from 0.1 to 0.25 seconds for analysis. The extracted segment corresponds roughly to the first vowel, /ae/, in "MATLAB".
dt = 1/Fs; I0 = round(0.1/dt); Iend = round(0.25/dt); x = mtlb(I0:Iend);
Two common preprocessing steps applied to speech waveforms before linear predictive coding are windowing and pre-emphasis (highpass) filtering.
Window the speech segment using a Hamming window.
x1 = x.*hamming(length(x));
Apply a pre-emphasis filter. The pre-emphasis filter is a highpass all-pole (AR(1)) filter.
preemph = [1 0.63]; x1 = filter(1,preemph,x1);
Obtain the linear prediction coefficients. To specify the model order, use the general rule that the order is two times the expected number of formants plus 2. In the frequency range, [0,|Fs|/2], you expect three formants. Therefore, set the model order equal to 8. Find the roots of the prediction polynomial returned by lpc.
A = lpc(x1,8); rts = roots(A);
Because the LPC coefficients are real-valued, the roots occur in complex conjugate pairs. Retain only the roots with one sign for the imaginary part and determine the angles corresponding to the roots.
rts = rts(imag(rts)>=0); angz = atan2(imag(rts),real(rts));
Convert the angular frequencies in rad/sample represented by the angles to hertz and calculate the bandwidths of the formants.
The bandwidths of the formants are represented by the distance of the prediction polynomial zeros from the unit circle.
[frqs,indices] = sort(angz.*(Fs/(2*pi))); bw = -1/2*(Fs/(2*pi))*log(abs(rts(indices)));
Use the criterion that formant frequencies should be greater than 90 Hz with bandwidths less than 400 Hz to determine the formants.
nn = 1; for kk = 1:length(frqs) if (frqs(kk) > 90 && bw(kk) <400) formants(nn) = frqs(kk); nn = nn+1; end end formants
formants = 1×3
103 ×
0.8697 2.0265 2.7380
The first three formants are 869.70, 2026.49, and 2737.95 Hz.
References
[1] Snell, Roy C., and Fausto Milinazzo. "Formant location from LPC analysis data." IEEE® Transactions on Speech and Audio Processing. Vol. 1, Number 2, 1993, pp. 129-134.
[2] Loizou, Philipos C. "COLEA: A MATLAB Software Tool for Speech Analysis."