Airframe Trim and Linearize
This example shows how to trim and linearize an airframe using Simulink® Control Design™.
Designing an autopilot using classical design techniques requires linear models of the airframe pitch dynamics for a number of trimmed flight conditions. MATLAB® can determine the trim conditions and derive linear state-space models directly from the nonlinear Simulink® and Aerospace Blockset™ model. This saves time and helps to validate the model. The functions provided by Simulink Control Design allow you to visualize the behavior of the airframe in terms of open-loop frequency (or time) responses.
Initialize Guidance Model
The first problem is to find the elevator deflection, and the resulting trimmed body rate (q), which will generate a given incidence value when the missile is traveling at a set speed. Once the trim condition is found, a linear model can be derived for the dynamics of the perturbations in the states around the trim condition.
open_system('AirframeTrim');
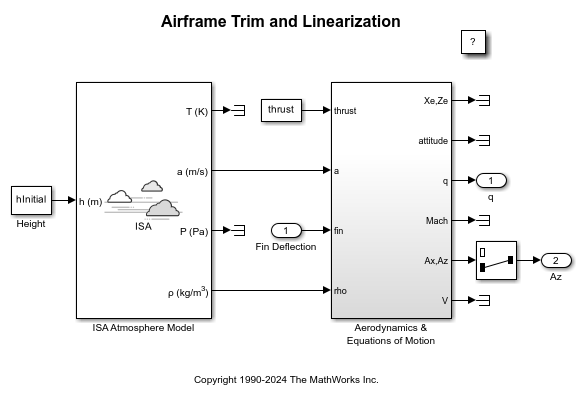
Define State Values
hInitial = 10000/m2ft; % Trim Height [m] MInitial = 3; % Trim Mach Number alphaInitial = -10*d2r; % Trim Incidence [rad] thetaInitial = 0*d2r; % Trim Flightpath Angle [rad] vInitial = MInitial*(340+(295-340)*hInitial/11000); % Total Velocity [m/s] qInitial = 0; % Initial pitch Body Rate [rad/sec]
Set Operating Point and State Specifications
The first state specifications are Position states, the second state specification is Theta. Both are known, but not at steady state. The third state specifications are body axis angular rates of which the variable w is at steady state.
opspec = operspec('AirframeTrim');
opspec.States(1).Known = [1;1];
opspec.States(1).SteadyState = [0;0];
opspec.States(2).Known = 1;
opspec.States(2).SteadyState = 0;
opspec.States(3).Known = [1 1];
opspec.States(3).SteadyState = [0 1];
Search for Operating Point, Set I/O, Then Linearize
op = findop('AirframeTrim',opspec); io(1) = linio('AirframeTrim/Fin Deflection',1,'input'); io(2) = linio('AirframeTrim/Selector',1,'output'); io(3) = linio(sprintf(['AirframeTrim/Aerodynamics &\n', ... 'Equations of Motion']),3,'output'); sys = linearize('AirframeTrim',op,io);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model AirframeTrim.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
__________ __________ __________ __________ __________ __________
(1.) AirframeTrim/Aerodynamics & Equations of Motion/3DOF (Body Axes)/Position
0 0 0 -Inf 967.6649 Inf
-3047.9999 -3047.9999 -3047.9999 -Inf -170.6254 Inf
(2.) AirframeTrim/Aerodynamics & Equations of Motion/3DOF (Body Axes)/Theta
0 0 0 -Inf -0.21604 Inf
(3.) AirframeTrim/Aerodynamics & Equations of Motion/3DOF (Body Axes)/U,w
967.6649 967.6649 967.6649 -Inf -14.0977 Inf
-170.6254 -170.6254 -170.6254 0 -7.439e-08 0
(4.) AirframeTrim/Aerodynamics & Equations of Motion/3DOF (Body Axes)/q
-Inf -0.21604 Inf 0 3.3582e-08 0
Inputs:
----------
Min u Max
_______ _______ _______
(1.) AirframeTrim/Fin Deflection
-Inf 0.13615 Inf
Outputs:
----------
Min y Max
__________ __________ __________
(1.) AirframeTrim/q
-Inf -0.21604 Inf
(2.) AirframeTrim/Az
-Inf -7.439e-08 Inf
Select Trimmed States, Create LTI Object, and Plot Bode Response
airframe = ss(sys.A(3:4,3:4),sys.B(3:4,:),sys.C(:,3:4),sys.D); set(airframe,'inputname',{'Elevator'}, ... 'outputname',[{'az'} {'q'}]); ltiview('bode',airframe); bdclose('AirframeTrim');
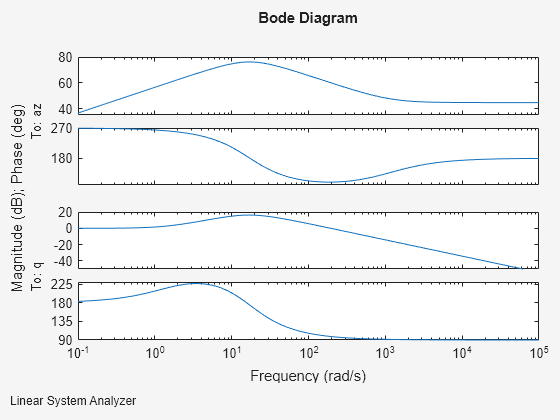

See Also
Topics
- Aerospace Blockset
- Create Aerospace Models (Aerospace Blockset)