Derivative
Compute approximate continuous derivative of continuous input signal with respect to time
Libraries:
Simulink /
Continuous
Description
The Derivative block approximates the continuous derivative of the continuous input signal u with respect to the simulation time t. Use the Derivative block when you need to compute the derivative for a differentiable signal that has continuous sample time.
Improper use of the Derivative block can lead to inaccuracies in simulation results. When possible, consider these alternatives to the Derivative block:
Rearrange the system equations to solve for an integral instead of a derivative. Then, structure the model based on the new equations so that the software integrates using blocks such as the Integrator block instead of differentiating.
For an example, see Best-Form Mathematical Models.
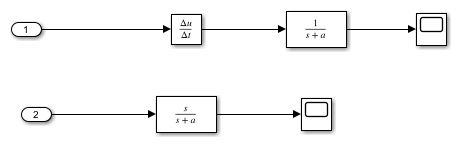
When a Transfer Fcn block also acts on the input or output signal of the Derivative block, implement the derivative for the signal by adding a zero in the transfer function instead.
To compute the finite difference, or difference quotient, for a discrete signal in a discrete system, use the Discrete Derivative block.
When you must use the Derivative block, use the block with only differentiable input signals that have continuous sample time.
The software issues a warning when the signal connected to this port has discrete or fixed-in-minor sample time. (since R2023b)
While the software does not issue a warning when the input signal has constant sample time, tuning the signal value introduces a discontinuity in the input signal. Differentiating across these discontinuities creates spikes in the output signal.
To compute the finite difference, or difference quotient, for a discrete signal in a discrete system, use the Discrete Derivative block.
Ensure Accuracy of Continuous Derivative Approximation
When you use the Derivative block, you must ensure that the accuracy of the block output signal satisfies your requirements. Even when used in an appropriate context, the accuracy of the Derivative block output signal depends on the step size and might depend on the dynamics of the rest of the system.
Use the Max step size parameter to prevent a variable-step solver from taking steps that are too large to satisfy your accuracy requirements. To choose an appropriate value for the maximum step size, you might need to run several simulations.
In variable-step simulations, the solver determines the size of the each major time step by monitoring the error in calculations of continuous states throughout the model. When the error in the calculated value for a continuous state exceeds the specified tolerance levels, the solver reduces the step size until the error falls within tolerance.
The Derivative block does not have any continuous states, so the solver cannot adjust the step size to ensure that the Derivative block calculations satisfy tolerance requirements. If the solver takes a large time step when the input signal value changes rapidly, the block might produce an unexpected output value.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
The Derivative block computes the numerical difference to approximate the continuous derivative where is the change in the input signal value and is the size of the major time step the solver took to reach the current simulation time. The accuracy of the continuous derivative approximation depends on the rate of change for the input signal and the step size.
The initial output value for the Derivative block is always
0. Taking the initial output value into consideration, this
equation represents the precise relationship between the block input and output
signals.
t is the current simulation time.
is the time of the last major time hit in the simulation.