Fuel Cell Stack
(To be removed) Implement generic hydrogen fuel cell stack model
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Sources
Description
The Fuel Cell Stack block implements a generic model parameterized to represent most popular types of fuel cell stacks fed with hydrogen and air.
The block represents two versions of the stack model: a simplified model and a detailed model. You can switch between the two models by selecting the level in the mask under Model detail level in the block dialog box.
Simplified Model
This model is based on the equivalent circuit of a fuel cell stack shown below:

The simplified model represents a particular fuel cell stack operating at nominal conditions of temperature and pressure. The parameters of the equivalent circuit can be modified based on the polarization curve obtained from the manufacturer datasheet. You just have to input in the mask the value of the voltage at 0 and 1 A, the nominal and the maximum operating points, for the parameters to be calculated. A typical polarization curve consists of three regions:
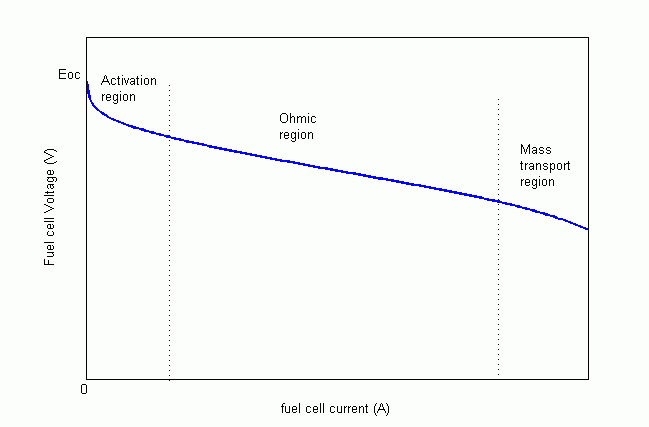
The first region represents the activation voltage drop due to the slowness of the chemical reactions taking place at electrode surfaces. Depending on the temperature and operating pressure, type of electrode, and catalyst used, this region is more or less wide. The second region represents the resistive losses due to the internal resistance of the fuel cell stack. Finally, the third region represents the mass transport losses resulting from the change in concentration of reactants as the fuel is used.
Detailed Model
The detailed model represents a particular fuel cell stack when the parameters such as pressures, temperature, compositions and flow rates of fuel and air vary. You can select which parameters to vary on the Signal variation pane on the block dialog box. These variations affect the open circuit voltage (Eoc), the exchange current (i0), and the Tafel slope (A). Eoc, i0 and A are modified as follows:
where:
R = 8.3145 J/(mol K)
F = 96485 A s/mol
z = Number of moving electrons
En = Nernst voltage, which is the thermodynamics voltage of the cells and depends on the temperatures and partial pressures of reactants and products inside the stack (V)
α = Charge transfer coefficient, which depends on the type of electrodes and catalysts used
PH2 = Partial pressure of hydrogen inside the stack (Pa)
PO2 = Partial pressure of oxygen inside the stack (Pa)
k = Boltzmann's constant = 1.38 × 10–23 J/K
h = Planck's constant = 6.626 × 10–34 J s
Δv = Activation barrier volume factor (m3). The size of activation barrier (ΔG) is computed assuming Δv = 1 m3.
ΔG = Size of the activation barrier which depends on the type of electrode and catalyst used (J/mol)
T = Temperature of operation (K)
Kc = Voltage constant at nominal condition of operation
The equivalent circuit is the same as for the simplified model, except that the parameters Eoc, i0 and Α have to be updated on-line as shown below:

The rates of conversion (utilizations) of hydrogen (UfH2) and oxygen (UfO2) are determined in Block A as follows:
where
Pfuel = Absolute supply pressure of fuel (atm)
Pair = Absolute supply pressure of air (atm)
Vlpm(fuel) = Fuel flow rate (l/min)
Vlpm(air) = Air flow rate (l/min)
x = Percentage of hydrogen in the fuel (%)
y = Percentage of oxygen in the oxidant (%)
N = Number of cells
The 60000 constant comes from the conversion from the liter/min flow rate used in the model to m3/s (1 liter/min = 1/60000 m3/s).
The partial pressures and the Nernst voltage are determined in Block B as follows:
and
where
PH2O = Partial pressure of water vapor inside the stack (atm)
w = Percentage of water vapor in the oxidant (%)
From the partial pressures of gases and the Nernst voltage, the new values of the open circuit voltage (Eoc) and the exchange current (i0) can be calculated.
Block C calculates the new value of the Tafel slope (A).
The parameters α, ΔG, and Kc are calculated based on the polarization curve at nominal conditions of operation along with some additional parameters, such as the low heating value (LHV) efficiency of the stack, composition of fuel and air, supply pressures and temperatures. They can be easily obtained from the manufacturer datasheet.
The nominal rates of conversion of gases are calculated as follows:
where:
ηnom = Nominal LHV efficiency of the stack (%).
Δh0(H2O(gas)) = 241.83 × 103 J/mol.
Vnom = Nominal voltage (V).
Inom = Nominal current (A).
Vlpm(air)nom = Nominal air flow rate (l/min).
Pairnom = Nominal absolute air supply pressure (Pa).
Tnom = Nominal operating temperature (K).
From these rates of conversion, the nominal partial pressures of gases and the Nernst voltage can be derived. With Eoc, i0 and Α known and assuming that the stack operates at constant rates of conversion or utilizations at nominal condition, α, ΔG, and Kc can be determined.
The dynamics of the fuel cell are represented if you specify the response time and the parameters for flow dynamics (peak utilization and corresponding voltage undershoot) on the Fuel Cell Dynamics pane on the dialog box.
The response time (Td) @ 95% is used to model the "charge double layer" phenomenon due to the build-up of charges at electrode/electrolyte interface. This affects only the activation voltage (NAln(ifc/i0)) as shown on the equivalent circuits.
The peak utilization (UfO2(peak)) and the corresponding voltage undershoot (Vu) are used to model the effect of oxygen depletion (due to the air compressor delay) on the cell output voltage. The Nernst voltage is modified due to this effect as follows:
where
K = voltage undershoot constant
UfO2(nom) = nominal oxygen utilization
K is determined as follows:
Current step and interrupt tests must be made on a real stack to represent with accuracy its dynamics. The figure below shows the stack response from these tests and the required parameters (Td, UfO2(peak) and Vu).
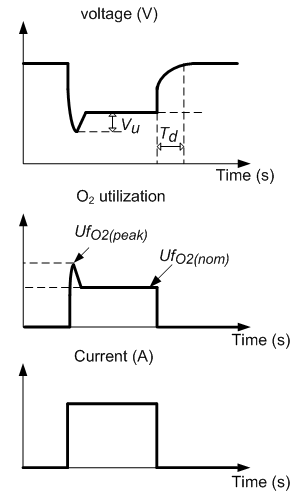
The response time (Td) depends on the fuel cell stack itself and is usually given on the datasheet. The parameters for flow dynamics (UfO2(peak) and Vu) depend on the dynamics of external equipment (compressor, regulator, and loads) and they are not provided by manufacturers as their values vary with the user application. For simulation, assume values of UfO2(peak) between 60% to 70% and Vu between 2-5% of the stack nominal voltage.
Assumptions and Limitations
These are the assumptions of this block:
The gases are ideal.
The stack is fed with hydrogen and air.
The stack is equipped with a cooling system which maintains the temperature at the cathode and anode exits stable and equal to the stack temperature.
The stack is equipped with a water management system to maintain the humidity inside the cell at appropriate level at any load.
The cell voltage drops are due to reaction kinetics and charge transport as most fuel cells do not operate in the mass transport region.
Pressure drops across flow channels are negligible.
The cell resistance is constant at any condition of operation.
These are the limitations of this block:
Chemical reaction dynamics caused by partial pressure changes of chemical species inside the cell are not considered.
The stack output power is limited by the fuel and air flow rates supplied.
The effect of temperature and humidity of the membrane on the internal resistance is not considered.
The flow of gases or water through the membrane is not considered.
Ports
Output
Conserving
Parameters
References
[1] Njoya, S. M., O. Tremblay, and L. -A. Dessaint. A generic fuel cell model for the simulation of fuel cell vehicles. Vehicle Power and Propulsion Conference, 2009, VPPC ’09, IEEE® . Sept. 7–10, 2009, pp. 1722–29.
[2] Motapon, S.N., O. Tremblay, and L. -A. Dessaint. “Development of a generic fuel cell model: application to a fuel cell vehicle simulation.” Int. J. of Power Electronics. Vol. 4, No. 6, 2012, pp. 505–22.

