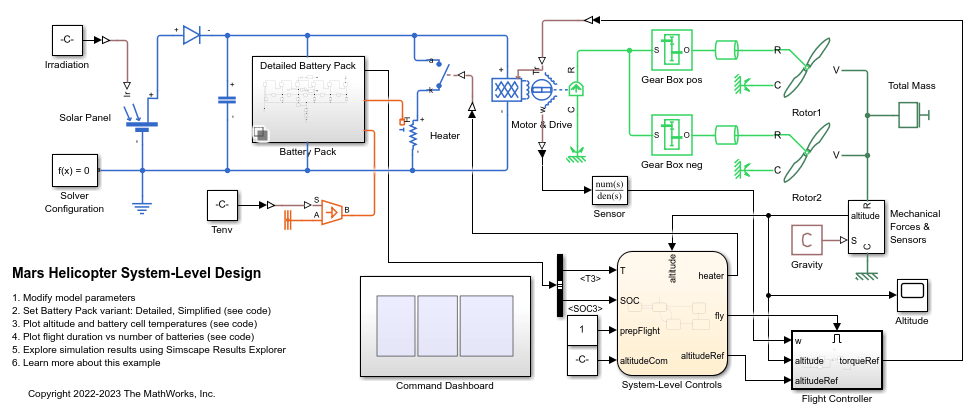
Battery (Table-Based)
Tabulated battery model
Libraries:
Simscape /
Electrical /
Sources
Simscape /
Battery /
Cells
Description
The Battery (Table-Based) block represents a high-fidelity battery model. The block calculates open-circuit voltage as a function of charge level and optional temperature using lookup tables and includes several modeling options:
Self-discharge
Battery fade
Charge dynamics
Calendar aging
Note
For all the table-based parameters, the Battery
(Table-Based) block supports linear interpolation only. For
extrapolation, set the Extrapolation method for all tables
parameter to either Nearest,
Linear, or Error.
For rows and columns, it follows the row-column convention, whereas rows are indexed first and, subsequently, columns.
The plot shows a battery whose performance varies with temperature and state of charge changes, as typically found on a datasheet.

Use this block to parameterize batteries with complex open-circuit voltage behavior from datasheets or experimental results. For a simpler representation of a battery, see the Battery block.
The Battery (Table-Based) block has two optional ports that you can expose by setting the corresponding parameters. The extra physical signal port, SOC, outputs the internal state of charge. Use this functionality to change the load behavior as a function of state of charge, without the complexity of building a charge state estimator. To expose the SOC port, in the Main setting, set the Expose SOC measurement port parameter to Yes.
To expose the thermal port, in the Thermal setting, set the Thermal port parameter to Model. The thermal port represents the battery thermal mass.
You can also choose different built-in parameterizations for this block. For more information, see the Predefined Parameterization section.
The battery equivalent circuit is made up of the fundamental battery model, the self-discharge resistance RSD, the charge dynamics model, and the series resistance R0.
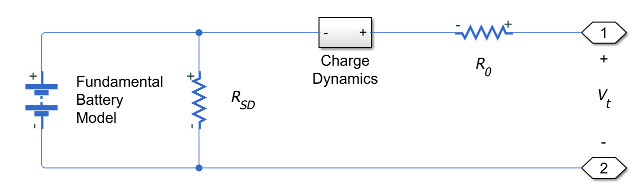
Battery Model
The block calculates the open-circuit voltage, or the voltage across the fundamental battery model by interpolation:
Where:
v0 is the open-circuit voltage of the battery. Specify the grid of lookup values using the Open-circuit voltage, V0(SOC,T) parameter if tabulating parameters over temperature, or Open-circuit voltage, V0(SOC) otherwise.
SOCis the ratio of current charge to nominal battery capacity specified in the Cell capacity, AH parameter along with the effects of the temperature dependent fade percentage change in cell capacity, δAH(n, Tfade), specified in the Percentage change in cell capacity, dAH(N, Tfade) parameter. Specify the SOC breakpoints using the Vector of state-of-charge values, SOC parameter. The block estimates the nominal battery capacity based on the number of cycles and the temperature of the battery by interpolating the specified temperature dependent fade characteristic and the Cell capacity, AH parameter.SOCrepresents the normalized data with respect to qnom.For the lookup-table based fade characteristic option,
For the equation-based fade characteristic option,
Finally,
SOCis obtained from the following equation.Where:
qnom is the cell capacity of the battery. Specify this value using the Cell capacity, AH parameter.
N is the reference number of discharge cycles over which you specify percent change of several battery parameters. Set this value using the Number of discharge cycles, N parameter.
n is the present number of cycles of the battery.
δAH is the percentage change in cell capacity of the battery after N discharge cycles.
T is the battery temperature. Specify the T breakpoints using the Vector of temperatures, T parameter if tabulating the parameters over temperature.
The block also models the series resistance R0 as a function of state of charge and optional temperature. Specify the grid of lookup values for the series resistance using the Terminal resistance, R0(SOC,T) parameter if tabulating the parameters over temperature, or Terminal resistance, R0(SOC) otherwise.
Modeling Self-Discharge
When the battery terminals are open-circuit, it is still possible for internal currents to discharge the battery. This behavior is called self-discharge. To enable this effect, set the Self-discharge parameter to Enabled.
The block models these internal currents with a temperature-dependent resistance RSD(T) across the terminals of the fundamental battery model. You can specify the lookup values for this resistance using the Self-discharge resistance, Rleak(T) parameter if tabulating the parameters over temperature, or Self-discharge resistance, Rleak otherwise.
Modeling Charge Dynamics
Batteries are not able to respond instantaneously to load changes. They require some time to achieve a steady-state. This time-varying property is a result of battery charge dynamics and is modeled using parallel RC sections in the equivalent circuit.
You can model battery charge dynamics using the Charge dynamics parameter:
No dynamics— The equivalent circuit contains no parallel RC sections. There is no delay between terminal voltage and internal charging voltage of the battery.One time-constant dynamics— The equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant, tau1(SOC,T) parameter if tabulating parameters over temperature or First time constant, tau1(SOC) otherwise.Two time-constant dynamics— The equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant, tau1(SOC,T) and Second time constant, tau2(SOC,T) parameters if tabulating parameters over temperature or First time constant, tau1(SOC) and Second time constant, tau2(SOC) otherwise.Three time-constant dynamics— The equivalent circuit contains three parallel RC sections. Specify the time constants using the First time constant, tau1(SOC,T), Second time constant, tau2(SOC,T), and Third time constant, tau3(SOC,T) parameters if tabulating parameters over temperature or First time constant, tau1(SOC), Second time constant, tau2(SOC), and Third time constant, tau3(SOC) otherwise.Four time-constant dynamics— The equivalent circuit contains four parallel RC sections. Specify the time constants using the First time constant, tau1(SOC,T), Second time constant, tau2(SOC,T), Third time constant, tau3(SOC,T), and Fourth time constant, tau4(SOC,T) parameters if tabulating parameters over temperature or First time constant, tau1(SOC), Second time constant, tau2(SOC), Third time constant, tau3(SOC), and Fourth time constant, tau4(SOC) otherwise.Five time-constant dynamics— The equivalent circuit contains five parallel RC sections. Specify the time constants using the First time constant, tau1(SOC,T), Second time constant, tau2(SOC,T), Third time constant, tau3(SOC,T), Fourth time constant, tau4(SOC,T), and Fifth time constant, tau5(SOC,T) parameters if tabulating parameters over temperature or First time constant, tau1(SOC), Second time constant, tau2(SOC), Third time constant, tau3(SOC), Fourth time constant, tau4(SOC), and Fifth time constant, tau5(SOC) otherwise.
This diagram shows the equivalent circuit for the block configured with two time-constant dynamics.

In the diagram:
R1 and R2 are the parallel RC resistances. Specify these values with the First polarization resistance, R1(SOC,T) and Second polarization resistance, R2(SOC,T) parameters, respectively, if tabulating parameters over temperature or First polarization resistance, R1(SOC) and Second polarization resistance, R2(SOC) otherwise.
C1 and C2 are the parallel RC capacitances. The time constant τ for each parallel section relates the R and C values using the relationship . Specify τ for each section using the First time constant, tau1(SOC,T) and Second time constant, tau2(SOC,T) parameters, respectively, if tabulating parameters over temperature or First time constant, tau1(SOC) and Second time constant, tau2(SOC) otherwise.
R0 is the series resistance. Specify this value with the Terminal resistance, R0(SOC,T) parameter if tabulating parameters over temperature or Terminal resistance, R0(SOC) otherwise.
Modeling Battery Fade
Battery fade is the deterioration of battery performance over repeated charge and discharge cycles. When the Fade characteristic parameter is set to Equations, the battery fade is modeled as follows.
The open-circuit voltage across the fundamental battery model fades proportionally with the number of discharge cycles n:
Where δv0 is the percent change in open-circuit voltage after N discharge cycles. Specify δv0 using the Change in open-circuit voltage after N discharge cycles (%) parameter.
Note
The Battery (Table-Based) block tracks the current and integrates it over time. The number of discharge cycles n increases by 1 every time an equivalent cell discharge capacity is extracted.
The nominal charge, from which state of charge is calculated, fades with the square root of number of discharge cycles:
All resistances in the battery model also fade with the square root of the number of discharge cycles:
Where:
Ri is the ith resistance
δRi is the percent change in this resistance over N cycles
Depending on how you have configured the block, the resistances might include:
The series resistance — Specify the percent change over N cycles using the Change in terminal resistance after N discharge cycles (%) parameter.
The self-discharge resistance — Specify the percent change over N cycles using the Change in self-discharge resistance after N discharge cycles (%) parameter.
The first charge dynamics resistance — Specify the percent change over N cycles using the Change in first polarization resistance after N discharge cycles (%) parameter.
The second charge dynamics resistance — Specify the percent change over N cycles using the Change in second polarization resistance after N discharge cycles (%) parameter.
The third charge dynamics resistance — Specify the percent change over N cycles using the Change in third polarization resistance after N discharge cycles (%) parameter.
The fourth charge dynamics resistance — Specify the percent change over N cycles using the Change in fourth polarization resistance after N discharge cycles (%) parameter.
The fifth charge dynamics resistance — Specify the percent change over N cycles using the Change in fifth polarization resistance after N discharge cycles (%) parameter.
Note
You can also model the battery fade characteristic by using lookup tables (temperature independent) or lookup tables (constant temperature dependent). Choosing any of these two options changes the blocks parameters accordingly. For more information, see the Fade parameters tab.
Modeling Thermal Effects
The battery temperature is determined from a summation of all the ohmic losses included in the model:
Where:
Mth is the battery thermal mass.
i corresponds to the ith ohmic loss contributor. Depending on how you have configured the block, the losses might include:
The series resistance
The self-discharge resistance
The first charge dynamics segment
The second charge dynamics segment
The third charge dynamics segment
The fourth charge dynamics segment
The fifth charge dynamics segment
VT,i is the voltage drop across resistor i.
RT,i is resistor i.
Modeling Battery Aging
You can model the battery performance deterioration that occurs when the battery is not used. Calendar aging affects both the internal resistance and capacity. In particular, the resistance increase depends by various mechanisms such as the creation of Solid Electrolyte Interface (SEI) at both anode and cathode and the corrosion of the current collector. These processes mainly depends on the storage temperature, the storage state of charge, and time.
You can model the calendar aging in the Battery (Table-Based) block by setting the Modeling option parameter to:
Equation-basedTabulated: temperatureTabulated: time and temperature
Note
The Battery (Table-Based) block only applies the calendar aging
during initialization. When you set the Internal resistance calendar
aging or Capacity calendar aging parameters
to Enabled, the block exposes the Vector of
time intervals parameter that represents the time the battery has
aged before the start of the simulation. Calendar aging during the simulation is
not covered with this option.
This equation defines the terminal resistance increase of the battery due to calendar aging:
where:
Voc is the Normalized open-circuit voltage during storage, V/Vnom.
R0 is the Internal resistance.
ti is the time sample derived from the Vector of time intervals parameter.
Ti is derived from the Vector of temperatures, T parameter.
b is the Terminal resistance linear scaling for voltage, b.
c is the Terminal resistance constant offset for voltage, c.
d is the Terminal resistance temperature-dependent exponential increase, d.
a is the Terminal resistance time exponent, a.
q is the electron's elementary charge, in C.
k is the Boltzmann constant, in J/K.
This equation defines the capacity decrease of the battery due to calendar aging:
where:
C0 is the initial capacity.
b is the Capacity linear scaling for voltage, b.
c is the Capacity constant offset for voltage, c.
d is the Capacity temperature-dependent exponential increase, d.
a is the Capacity time constant, a.
If you set the Storage condition parameter to Specify state-of-charge during storage, the block converts the state of charge during storage into normalized open-circuit voltage using the tabulated voltage V0 against the state of charge and the temperature during storage.
The aged terminal resistance is the product between the terminal resistance, R0(SOC,T), the percentage resistance increase, dR0, and the power law that describes the time dependence of the calendar aging:
where:
T is the battery temperature. Specify the T breakpoints using the Vector of temperatures, T parameter if tabulating the parameters over temperature.
Tst is the Vector of storage temperatures.
tst,i and tst,i-1 are the time samples derived from the Vector of time intervals.
t0 is assumed to be null.
tst,m is the moment in time at which the resistance increase, dR0, is measured.
The same equation applies to the calculation of the aged battery capacity.
The aged terminal resistance is the product between the terminal resistance, R0(SOC,T) and dR0:
The same equation applies to the calculation of the aged battery capacity.
Predefined Parameterization
There are multiple available built-in parameterizations for the Battery (Table-Based) block.
This pre-parameterization data allows you to set up the block to represent components by specific suppliers. The parameterizations of these batteries match the discharge curves in the manufacturer data sheets. To load a predefined parameterization, double-click the Battery (Table-Based) block, click the <click to select> hyperlink of the Selected part parameter and, in the Block Parameterization Manager window, select the part you want to use from the list of available components.
The available pre-parameterized data model steady state electrical parameters of a lithium-ion battery. The Open-circuit voltage, V0(SOC), Terminal resistance, R0(SOC, T), Cell capacity, AH, Percentage change in cell capacity, dAH, and Percentage change in Open-circuit voltage, dV0(N) parameters are parameterized from characteristics curves in the manufacture datasheets. The change in series resistance with the battery cycle life, the thermal mass, and the dynamic RC network parameters are not parameterized. Instead, the net resistance of the RC network resistors is summed to the series resistance of the specific pre-parameterized data. If you need to fill the RC parameter data, subtract the net RC network resistance from the series resistance data.
The available data is parameterized for 1C discharge current for different temperatures up to the minimum terminal voltage in the datasheet. The data below the minimum terminal voltage is extrapolated. The Open-circuit voltage, V0(SOC) parameter is approximated to be temperature independent. At lower temperature, in the low SOC region, the terminal resistances are constant and equal to the value of the resistance at the minimum terminal voltage. This might lead to higher thermal losses.
Note
The predefined parameterizations of Simscape™ components use available data sources for the parameter values. Engineering judgment and simplifying assumptions are used to fill in for missing data. As a result, expect deviations between simulated and actual physical behavior. To ensure accuracy, validate the simulated behavior against experimental data and refine component models as necessary.
For more information about pre-parameterization and for a list of the available components, see List of Pre-Parameterized Components.
Plot Basic Voltage-Charge Characteristics
You can plot the basic voltage-charge characteristics of the Battery (Table-Based) block without building a complete model. Use the plots to explore the impact of your parameter choices on device characteristics. If you parameterize the block from a datasheet, you can compare your plots to the datasheet to check that you parameterized the block correctly. If you have a complete working model but do not know which manufactured part to use, you can compare your plots to datasheets to help you decide.
To plot the basic characteristics, right-click the block and select Battery > Basic characteristics from the context menu. For more information about the Basic characteristics option, see Plot Basic Voltage-Charge Characteristics of Battery Blocks.
Examples
Ports
Output
Conserving
Parameters
References
[1] Tarun, H., M. Ceraolo, J. Gazzarri, and R. Jackey. “High Fidelity Electrical Model with Thermal Dependence for Characterization and Simulation of High Power Lithium Battery Cells.” In 2012 IEEE International Electric Vehicle Conference, 1–8, 2012. https://doi.org/10.1109/IEVC.2012.6183271.
[2] Schmalstieg, J., S. Käbitz, M. Ecker, and D. U. Sauer. “A Holistic Aging Model for Li(NiMnCo)O2 Based 18650 Lithium-Ion Batteries.” Journal of Power Sources 257 (July 2014): 325–334. https://doi.org/10.1016/j.jpowsour.2014.02.012.
[3] Zhang, R., and Z. Pan. “Model Identification of Lithium-Ion Batteries Considering Current-Rate Effects on Battery Impedance.” In 2019 4th International Conference on Power and Renewable Energy (ICPRE), 305–309, 2019. https://doi.org/10.1109/ICPRE48497.2019.9034704.
[4] Baronti, F., N. Femia, R. Saletti, C. Visone, and W. Zamboni. “Hysteresis Modeling in Li-Ion Batteries.” IEEE Transactions on Magnetics 50, no. 11 (November 2014): 1–4. https://doi.org/10.1109/TMAG.2014.2323426.
[5] Baronti, F., W. Zamboni, N. Femia, R. Roncella, and R. Saletti. “Experimental Analysis of Open-Circuit Voltage Hysteresis in Lithium-Iron-Phosphate Batteries.” In IECON 2013 - 39th Annual Conference of the IEEE Industrial Electronics Society, 6728–6733, 2013. https://doi.org/10.1109/IECON.2013.6700246.