fitcnb
Train multiclass naive Bayes model
Syntax
Description
Mdl = fitcnb(Tbl,ResponseVarName)Mdl), trained
by the predictors in table Tbl and class labels
in the variable Tbl.ResponseVarName.
Mdl = fitcnb(___,Name,Value)Name,Value pair arguments, using any
of the previous syntaxes. For example, you can specify a distribution
to model the data, prior probabilities for the classes, or the kernel
smoothing window bandwidth.
[
also returns Mdl,AggregateOptimizationResults] = fitcnb(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments.
You must also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this
syntax to optimize on compact model size instead of cross-validation loss, and
to perform a set of multiple optimization problems that have the same options
but different constraint bounds.
Note
For a list of supported syntaxes when the input variables are tall arrays, see Tall Arrays.
Examples
Load Fisher's iris data set.
load fisheriris
X = meas(:,3:4);
Y = species;
tabulate(Y) Value Count Percent
setosa 50 33.33%
versicolor 50 33.33%
virginica 50 33.33%
The software can classify data with more than two classes using naive Bayes methods.
Train a naive Bayes classifier. It is good practice to specify the class order.
Mdl = fitcnb(X,Y,'ClassNames',{'setosa','versicolor','virginica'})
Mdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
DistributionNames: {'normal' 'normal'}
DistributionParameters: {3×2 cell}
Properties, Methods
Mdl is a trained ClassificationNaiveBayes classifier.
By default, the software models the predictor distribution within each class using a Gaussian distribution having some mean and standard deviation. Use dot notation to display the parameters of a particular Gaussian fit, e.g., display the fit for the first feature within setosa.
setosaIndex = strcmp(Mdl.ClassNames,'setosa');
estimates = Mdl.DistributionParameters{setosaIndex,1}estimates = 2×1
1.4620
0.1737
The mean is 1.4620 and the standard deviation is 0.1737.
Plot the Gaussian contours.
figure gscatter(X(:,1),X(:,2),Y); h = gca; cxlim = h.XLim; cylim = h.YLim; hold on Params = cell2mat(Mdl.DistributionParameters); Mu = Params(2*(1:3)-1,1:2); % Extract the means Sigma = zeros(2,2,3); for j = 1:3 Sigma(:,:,j) = diag(Params(2*j,:)).^2; % Create diagonal covariance matrix xlim = Mu(j,1) + 4*[-1 1]*sqrt(Sigma(1,1,j)); ylim = Mu(j,2) + 4*[-1 1]*sqrt(Sigma(2,2,j)); f = @(x,y) arrayfun(@(x0,y0) mvnpdf([x0 y0],Mu(j,:),Sigma(:,:,j)),x,y); fcontour(f,[xlim ylim]) % Draw contours for the multivariate normal distributions end h.XLim = cxlim; h.YLim = cylim; title('Naive Bayes Classifier -- Fisher''s Iris Data') xlabel('Petal Length (cm)') ylabel('Petal Width (cm)') legend('setosa','versicolor','virginica') hold off

You can change the default distribution using the name-value pair argument 'DistributionNames'. For example, if some predictors are categorical, then you can specify that they are multivariate, multinomial random variables using 'DistributionNames','mvmn'.
Construct a naive Bayes classifier for Fisher's iris data set. Also, specify prior probabilities during training.
Load Fisher's iris data set.
load fisheriris X = meas; Y = species; classNames = {'setosa','versicolor','virginica'}; % Class order
X is a numeric matrix that contains four measurements for 150 irises. Y is a cell array of character vectors that contains the corresponding iris species.
By default, the prior class probability distribution is the relative frequency distribution of the classes in the data set. In this case the prior probability is 33% for each species. However, suppose you know that in the population 50% of the irises are setosa, 20% are versicolor, and 30% are virginica. You can incorporate this information by specifying this distribution as a prior probability during training.
Train a naive Bayes classifier. Specify the class order and prior class probability distribution.
prior = [0.5 0.2 0.3]; Mdl = fitcnb(X,Y,'ClassNames',classNames,'Prior',prior)
Mdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
DistributionNames: {'normal' 'normal' 'normal' 'normal'}
DistributionParameters: {3×4 cell}
Properties, Methods
Mdl is a trained ClassificationNaiveBayes classifier, and some of its properties appear in the Command Window. The software treats the predictors as independent given a class, and, by default, fits them using normal distributions.
The naive Bayes algorithm does not use the prior class probabilities during training. Therefore, you can specify prior class probabilities after training using dot notation. For example, suppose that you want to see the difference in performance between a model that uses the default prior class probabilities and a model that uses different prior.
Create a new naive Bayes model based on Mdl, and specify that the prior class probability distribution is an empirical class distribution.
defaultPriorMdl = Mdl;
FreqDist = cell2table(tabulate(Y));
defaultPriorMdl.Prior = FreqDist{:,3};The software normalizes the prior class probabilities to sum to 1.
Estimate the cross-validation error for both models using 10-fold cross-validation.
rng(1); % For reproducibility
defaultCVMdl = crossval(defaultPriorMdl);
defaultLoss = kfoldLoss(defaultCVMdl)defaultLoss = 0.0533
CVMdl = crossval(Mdl); Loss = kfoldLoss(CVMdl)
Loss = 0.0340
Mdl performs better than defaultPriorMdl.
Load Fisher's iris data set.
load fisheriris
X = meas;
Y = species;Train a naive Bayes classifier using every predictor. It is good practice to specify the class order.
Mdl1 = fitcnb(X,Y,... 'ClassNames',{'setosa','versicolor','virginica'})
Mdl1 =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
DistributionNames: {'normal' 'normal' 'normal' 'normal'}
DistributionParameters: {3×4 cell}
Properties, Methods
Mdl1.DistributionParameters
ans=3×4 cell array
{2×1 double} {2×1 double} {2×1 double} {2×1 double}
{2×1 double} {2×1 double} {2×1 double} {2×1 double}
{2×1 double} {2×1 double} {2×1 double} {2×1 double}
Mdl1.DistributionParameters{1,2}ans = 2×1
3.4280
0.3791
By default, the software models the predictor distribution within each class as a Gaussian with some mean and standard deviation. There are four predictors and three class levels. Each cell in Mdl1.DistributionParameters corresponds to a numeric vector containing the mean and standard deviation of each distribution, e.g., the mean and standard deviation for setosa iris sepal widths are 3.4280 and 0.3791, respectively.
Estimate the confusion matrix for Mdl1.
isLabels1 = resubPredict(Mdl1); ConfusionMat1 = confusionchart(Y,isLabels1);
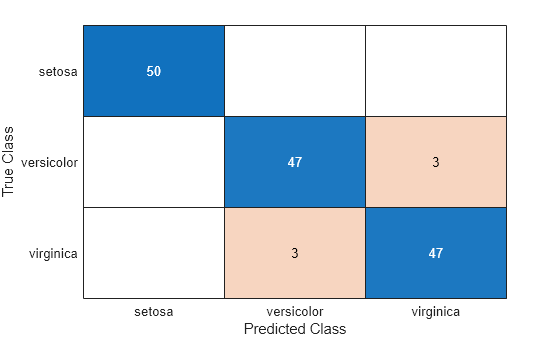
Element (j, k) of the confusion matrix chart represents the number of observations that the software classifies as k, but are truly in class j according to the data.
Retrain the classifier using the Gaussian distribution for predictors 1 and 2 (the sepal lengths and widths), and the default normal kernel density for predictors 3 and 4 (the petal lengths and widths).
Mdl2 = fitcnb(X,Y,... 'DistributionNames',{'normal','normal','kernel','kernel'},... 'ClassNames',{'setosa','versicolor','virginica'}); Mdl2.DistributionParameters{1,2}
ans = 2×1
3.4280
0.3791
The software does not train parameters to the kernel density. Rather, the software chooses an optimal width. However, you can specify a width using the 'Width' name-value pair argument.
Estimate the confusion matrix for Mdl2.
isLabels2 = resubPredict(Mdl2); ConfusionMat2 = confusionchart(Y,isLabels2);
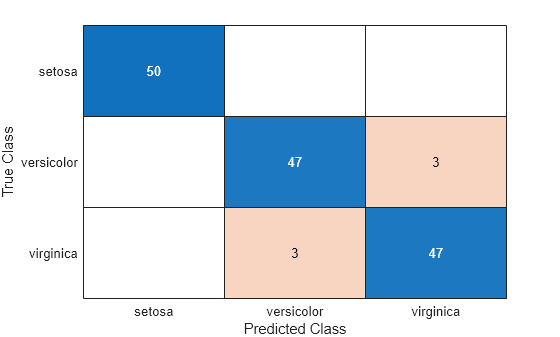
Based on the confusion matrices, the two classifiers perform similarly in the training sample.
Load Fisher's iris data set.
load fisheriris X = meas; Y = species; rng(1); % For reproducibility
Train and cross-validate a naive Bayes classifier using the default options and k-fold cross-validation. It is good practice to specify the class order.
CVMdl1 = fitcnb(X,Y,... 'ClassNames',{'setosa','versicolor','virginica'},... 'CrossVal','on');
By default, the software models the predictor distribution within each class as a Gaussian with some mean and standard deviation. CVMdl1 is a ClassificationPartitionedModel model.
Create a default naive Bayes binary classifier template, and train an error-correcting, output codes multiclass model.
t = templateNaiveBayes(); CVMdl2 = fitcecoc(X,Y,'CrossVal','on','Learners',t);
CVMdl2 is a ClassificationPartitionedECOC model. You can specify options for the naive Bayes binary learners using the same name-value pair arguments as for fitcnb.
Compare the out-of-sample k-fold classification error (proportion of misclassified observations).
classErr1 = kfoldLoss(CVMdl1,'LossFun','ClassifErr')
classErr1 = 0.0533
classErr2 = kfoldLoss(CVMdl2,'LossFun','ClassifErr')
classErr2 = 0.0467
Mdl2 has a lower generalization error.
Some spam filters classify an incoming email as spam based on how many times a word or punctuation (called tokens) occurs in an email. The predictors are the frequencies of particular words or punctuations in an email. Therefore, the predictors compose multinomial random variables.
This example illustrates classification using naive Bayes and multinomial predictors.
Create Training Data
Suppose you observed 1000 emails and classified them as spam or not spam. Do this by randomly assigning -1 or 1 to y for each email.
n = 1000; % Sample size rng(1); % For reproducibility Y = randsample([-1 1],n,true); % Random labels
To build the predictor data, suppose that there are five tokens in the vocabulary, and 20 observed tokens per email. Generate predictor data from the five tokens by drawing random, multinomial deviates. The relative frequencies for tokens corresponding to spam emails should differ from emails that are not spam.
tokenProbs = [0.2 0.3 0.1 0.15 0.25;... 0.4 0.1 0.3 0.05 0.15]; % Token relative frequencies tokensPerEmail = 20; % Fixed for convenience X = zeros(n,5); X(Y == 1,:) = mnrnd(tokensPerEmail,tokenProbs(1,:),sum(Y == 1)); X(Y == -1,:) = mnrnd(tokensPerEmail,tokenProbs(2,:),sum(Y == -1));
Train the Classifier
Train a naive Bayes classifier. Specify that the predictors are multinomial.
Mdl = fitcnb(X,Y,'DistributionNames','mn');
Mdl is a trained ClassificationNaiveBayes classifier.
Assess the in-sample performance of Mdl by estimating the misclassification error.
isGenRate = resubLoss(Mdl,'LossFun','ClassifErr')
isGenRate = 0.0320
The in-sample misclassification rate is 2%.
Create New Data
Randomly generate deviates that represent a new batch of emails.
newN = 500; newY = randsample([-1 1],newN,true); newX = zeros(newN,5); newX(newY == 1,:) = mnrnd(tokensPerEmail,tokenProbs(1,:),... sum(newY == 1)); newX(newY == -1,:) = mnrnd(tokensPerEmail,tokenProbs(2,:),... sum(newY == -1));
Assess Classifier Performance
Classify the new emails using the trained naive Bayes classifier Mdl, and determine whether the algorithm generalizes.
oosGenRate = loss(Mdl,newX,newY)
oosGenRate = 0.0160
The out-of-sample misclassification rate is 2.6% indicating that the classifier generalizes fairly well.
This example shows how to use the OptimizeHyperparameters name-value pair to minimize cross-validation loss in a naive Bayes classifier using fitcnb. The example uses Fisher's iris data.
Load Fisher's iris data.
load fisheriris X = meas; Y = species; classNames = {'setosa','versicolor','virginica'};
Optimize the classification using the 'auto' parameters.
For reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function.
rng default Mdl = fitcnb(X,Y,'ClassNames',classNames,'OptimizeHyperparameters','auto',... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName',... 'expected-improvement-plus'))
|====================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Distribution-| Width | Standardize |
| | result | | runtime | (observed) | (estim.) | Names | | |
|====================================================================================================================|
| 1 | Best | 0.093333 | 0.44801 | 0.093333 | 0.093333 | kernel | 5.6939 | false |
| 2 | Accept | 0.13333 | 0.11282 | 0.093333 | 0.11333 | kernel | 94.849 | true |
| 3 | Best | 0.053333 | 0.067206 | 0.053333 | 0.05765 | normal | - | - |
| 4 | Accept | 0.053333 | 0.035338 | 0.053333 | 0.053336 | normal | - | - |
| 5 | Accept | 0.26667 | 0.082826 | 0.053333 | 0.053338 | kernel | 0.001001 | true |
| 6 | Accept | 0.093333 | 0.071459 | 0.053333 | 0.053337 | kernel | 10.043 | false |
| 7 | Accept | 0.26667 | 0.075464 | 0.053333 | 0.05334 | kernel | 0.0010132 | false |
| 8 | Accept | 0.093333 | 0.069784 | 0.053333 | 0.053338 | kernel | 985.05 | false |
| 9 | Accept | 0.13333 | 0.060409 | 0.053333 | 0.053338 | kernel | 993.63 | true |
| 10 | Accept | 0.053333 | 0.03106 | 0.053333 | 0.053336 | normal | - | - |
| 11 | Accept | 0.053333 | 0.023468 | 0.053333 | 0.053336 | normal | - | - |
| 12 | Best | 0.046667 | 0.086393 | 0.046667 | 0.046679 | kernel | 0.30205 | true |
| 13 | Accept | 0.11333 | 0.067386 | 0.046667 | 0.046685 | kernel | 1.3021 | true |
| 14 | Accept | 0.053333 | 0.065982 | 0.046667 | 0.046695 | kernel | 0.10521 | true |
| 15 | Accept | 0.046667 | 0.064699 | 0.046667 | 0.046677 | kernel | 0.25016 | false |
| 16 | Accept | 0.06 | 0.062682 | 0.046667 | 0.046686 | kernel | 0.58328 | false |
| 17 | Accept | 0.046667 | 0.093038 | 0.046667 | 0.046656 | kernel | 0.07969 | false |
| 18 | Accept | 0.093333 | 0.070307 | 0.046667 | 0.046654 | kernel | 131.33 | false |
| 19 | Accept | 0.046667 | 0.060383 | 0.046667 | 0.04648 | kernel | 0.13384 | false |
| 20 | Best | 0.04 | 0.059662 | 0.04 | 0.040132 | kernel | 0.19525 | true |
|====================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Distribution-| Width | Standardize |
| | result | | runtime | (observed) | (estim.) | Names | | |
|====================================================================================================================|
| 21 | Accept | 0.04 | 0.078294 | 0.04 | 0.040066 | kernel | 0.19458 | true |
| 22 | Accept | 0.04 | 0.069381 | 0.04 | 0.040043 | kernel | 0.19601 | true |
| 23 | Accept | 0.04 | 0.073037 | 0.04 | 0.040031 | kernel | 0.19412 | true |
| 24 | Accept | 0.10667 | 0.064984 | 0.04 | 0.040018 | kernel | 0.0084391 | true |
| 25 | Accept | 0.073333 | 0.062139 | 0.04 | 0.040022 | kernel | 0.02769 | false |
| 26 | Accept | 0.04 | 0.064822 | 0.04 | 0.04002 | kernel | 0.2037 | true |
| 27 | Accept | 0.13333 | 0.061307 | 0.04 | 0.040021 | kernel | 12.501 | true |
| 28 | Accept | 0.11333 | 0.057437 | 0.04 | 0.040006 | kernel | 0.0048728 | false |
| 29 | Accept | 0.1 | 0.057983 | 0.04 | 0.039993 | kernel | 0.028653 | true |
| 30 | Accept | 0.046667 | 0.057854 | 0.04 | 0.041008 | kernel | 0.18725 | true |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 7.4665 seconds
Total objective function evaluation time: 2.3556
Best observed feasible point:
DistributionNames Width Standardize
_________________ _______ ___________
kernel 0.19525 true
Observed objective function value = 0.04
Estimated objective function value = 0.041117
Function evaluation time = 0.059662
Best estimated feasible point (according to models):
DistributionNames Width Standardize
_________________ ______ ___________
kernel 0.2037 true
Estimated objective function value = 0.041008
Estimated function evaluation time = 0.068318

Mdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
DistributionNames: {'kernel' 'kernel' 'kernel' 'kernel'}
DistributionParameters: {3×4 cell}
Kernel: {'normal' 'normal' 'normal' 'normal'}
Support: {'unbounded' 'unbounded' 'unbounded' 'unbounded'}
Width: [3×4 double]
Mu: [5.8433 3.0573 3.7580 1.1993]
Sigma: [0.8281 0.4359 1.7653 0.7622]
Properties, Methods
Input Arguments
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
Response variable name, specified as the name of a variable in
Tbl.
You must specify ResponseVarName as a character vector or string scalar.
For example, if the response variable Y is
stored as Tbl.Y, then specify it as
"Y". Otherwise, the software
treats all columns of Tbl, including
Y, as predictors when training
the model.
The response variable must be a categorical, character, or string array; a logical or numeric
vector; or a cell array of character vectors. If
Y is a character array, then each
element of the response variable must correspond to one row of
the array.
A good practice is to specify the order of the classes by using the
ClassNames name-value
argument.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Class labels to which the naive Bayes classifier is trained, specified as a categorical,
character, or string array, a logical or numeric vector, or a cell array of character
vectors. Each element of Y defines the class membership of the
corresponding row of X. Y supports
K class levels.
If Y is a character array, then each row
must correspond to one class label.
The length of Y and the number of rows of X must
be equivalent.
Data Types: categorical | char | string | logical | single | double | cell
Predictor data, specified as a numeric matrix.
Each row of X corresponds to one observation
(also known as an instance or example), and each column corresponds
to one variable (also known as a feature).
The length of Y and the number of rows of X must
be equivalent.
Data Types: double
Note:
The software treats NaN, empty character vector (''),
empty string (""), <missing>, and
<undefined> elements as missing data values.
If
Ycontains missing values, then the software removes them and the corresponding rows ofX.If
Xcontains any rows composed entirely of missing values, then the software removes those rows and the corresponding elements ofY.If
Xcontains missing values and you set'DistributionNames','mn', then the software removes those rows ofXand the corresponding elements ofY.If a predictor is not represented in a class, that is, if all of its values are
NaNwithin a class, then the software returns an error.
Removing rows of X and corresponding elements of
Y decreases the effective training or cross-validation sample
size.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'DistributionNames','mn','Prior','uniform','KSWidth',0.5
specifies that the data distribution is multinomial, the prior probabilities for all
classes are equal, and the kernel smoothing window bandwidth for all classes is
0.5 units.
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparameters name-value argument. You can modify the
cross-validation for OptimizeHyperparameters only by using the
HyperparameterOptimizationOptions name-value argument.
Naive Bayes Options
Data distributions fitcnb uses to model the data, specified as the
comma-separated pair consisting of 'DistributionNames' and a
character vector or string scalar, a string array, or a cell array of character vectors
with values from this table.
| Value | Description |
|---|---|
'kernel' | Kernel smoothing density estimate. |
'mn' | Multinomial distribution. If you specify mn,
then all features are components of a multinomial distribution.
Therefore, you cannot include 'mn' as an element
of a string array or a cell array of character vectors. For details,
see Algorithms. |
'mvmn' | Multivariate multinomial distribution. For details, see Algorithms. |
'normal' | Normal (Gaussian) distribution. |
If you specify a character vector or string scalar, then the software models all the features using that distribution. If you specify a 1-by-P string array or cell array of character vectors, then the software models feature j using the distribution in element j of the array.
By default, the software sets all predictors specified as categorical
predictors (using the CategoricalPredictors name-value
pair argument) to 'mvmn'. Otherwise, the default
distribution is 'normal'.
You must specify that at least one predictor has distribution 'kernel' to
additionally specify Kernel, Standardize,
Support, or Width.
Example: 'DistributionNames','mn'
Example: 'DistributionNames',{'kernel','normal','kernel'}
Kernel smoother type, specified as the comma-separated pair consisting of
'Kernel' and a character vector or string scalar, a string array,
or a cell array of character vectors.
This table summarizes the available options for setting the kernel smoothing density region. Let I{u} denote the indicator function.
| Value | Kernel | Formula |
|---|---|---|
'box' | Box (uniform) |
|
'epanechnikov' | Epanechnikov |
|
'normal' | Gaussian |
|
'triangle' | Triangular |
|
If you specify a 1-by-P string array or cell array, with each element of
the array containing any value in the table, then the software trains the classifier
using the kernel smoother type in element j for feature
j in X. The software ignores elements of
Kernel not corresponding to a predictor whose distribution is
'kernel'.
You must specify that at least one predictor has distribution 'kernel' to
additionally specify Kernel, Standardize,
Support, or Width.
Example: 'Kernel',{'epanechnikov','normal'}
Since R2023b
Flag to standardize the kernel-distributed predictors, specified as a numeric or
logical 0 (false) or 1
(true). This argument is valid only when the
DistributionNames value contains at least one kernel
distribution ("kernel").
If you set Standardize to true, then the
software centers and scales each kernel-distributed predictor variable by the
corresponding column mean and standard deviation. The software does not standardize
predictors with nonkernel distributions, such as categorical predictors.
Example: "Standardize",true
Data Types: single | double | logical
Kernel smoothing density support, specified as the comma-separated pair consisting of
'Support' and 'positive',
'unbounded', a string array, a cell array, or a numeric row
vector. The software applies the kernel smoothing density to the specified
region.
This table summarizes the available options for setting the kernel smoothing density region.
| Value | Description |
|---|---|
| 1-by-2 numeric row vector | For example, [L,U], where L and U are
the finite lower and upper bounds, respectively, for the density support. |
'positive' | The density support is all positive real values. |
'unbounded' | The density support is all real values. |
If you specify a 1-by-P string array or cell array, with
each element in the string array containing any text value in the table and each element
in the cell array containing any value in the table, then the software trains the
classifier using the kernel support in element j for feature
j in X. The software ignores elements of
Kernel not corresponding to a predictor whose distribution is
'kernel'.
You must specify that at least one predictor has distribution 'kernel' to
additionally specify Kernel, Standardize,
Support, or Width.
Example: 'Support',{[-10,20],'unbounded'}
Data Types: char | string | cell | double
Kernel smoothing window width, specified as the comma-separated
pair consisting of 'Width' and a matrix of numeric
values, numeric column vector, numeric row vector, or scalar.
Suppose there are K class levels and P predictors. This table summarizes the available options for setting the kernel smoothing window width.
| Value | Description |
|---|---|
| K-by-P matrix of numeric values | Element (k,j) specifies the width for predictor j in class k. |
| K-by-1 numeric column vector | Element k specifies the width for all predictors in class k. |
| 1-by-P numeric row vector | Element j specifies the width in all class levels for predictor j. |
| scalar | Specifies the bandwidth for all features in all classes. |
By default, the software selects
a default width automatically for each combination of predictor and
class by using a value that is optimal for a Gaussian distribution.
If you specify Width and it contains NaNs,
then the software selects widths for the elements containing NaNs.
You must specify that at least one predictor has distribution 'kernel' to
additionally specify Kernel, Standardize,
Support, or Width.
Example: 'Width',[NaN NaN]
Data Types: double | struct
Cross-Validation Options
Cross-validation flag, specified as the comma-separated pair
consisting of 'Crossval' and 'on'
or 'off'.
If you specify 'on', then the software implements
10-fold cross-validation.
To override this cross-validation setting, use one of these name-value
pair arguments: CVPartition,
Holdout, KFold, or
Leaveout. To create a cross-validated model,
you can use one cross-validation name-value pair argument at a time
only.
Alternatively, cross-validate later by passing
Mdl to crossval.
Example: 'CrossVal','on'
Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the
indexing for the training and validation sets.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Suppose you create a random partition for 5-fold cross-validation on 500
observations by using cvp = cvpartition(500,KFold=5). Then, you can
specify the cross-validation partition by setting
CVPartition=cvp.
Fraction of the data used for holdout validation, specified as a scalar value in the range
(0,1). If you specify Holdout=p, then the software completes these
steps:
Randomly select and reserve
p*100% of the data as validation data, and train the model using the rest of the data.Store the compact trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Holdout=0.1
Data Types: double | single
Number of folds to use in the cross-validated model, specified as a positive integer value
greater than 1. If you specify KFold=k, then the software completes
these steps:
Randomly partition the data into
ksets.For each set, reserve the set as validation data, and train the model using the other
k– 1 sets.Store the
kcompact trained models in ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: KFold=5
Data Types: single | double
Leave-one-out cross-validation flag, specified as "on" or
"off". If you specify Leaveout="on", then for
each of the n observations (where n is the number
of observations, excluding missing observations, specified in the
NumObservations property of the model), the software completes
these steps:
Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Leaveout="on"
Data Types: char | string
Other Classification Options
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the
predictor data is in a table (Tbl), fitcnb
assumes that a variable is categorical if it is a logical vector, categorical vector, character
array, string array, or cell array of character vectors. If the predictor data is a matrix
(X), fitcnb assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
For the identified categorical predictors, fitcnb
uses multivariate multinomial distributions. For details, see
DistributionNames and Algorithms.
Example: 'CategoricalPredictors','all'
Data Types: single | double | logical | char | string | cell
Names of classes to use for training, specified as a categorical, character, or string
array; a logical or numeric vector; or a cell array of character vectors.
ClassNames must have the same data type as the response variable
in Tbl or Y.
If ClassNames is a character array, then each element must correspond to one row of the array.
Use ClassNames to:
Specify the order of the classes during training.
Specify the order of any input or output argument dimension that corresponds to the class order. For example, use
ClassNamesto specify the order of the dimensions ofCostor the column order of classification scores returned bypredict.Select a subset of classes for training. For example, suppose that the set of all distinct class names in
Yis["a","b","c"]. To train the model using observations from classes"a"and"c"only, specifyClassNames=["a","c"].
The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.
Example: ClassNames=["b","g"]
Data Types: categorical | char | string | logical | single | double | cell
Cost of misclassification of a point, specified as the comma-separated
pair consisting of 'Cost' and one of the
following:
Square matrix, where
Cost(i,j)is the cost of classifying a point into classjif its true class isi(i.e., the rows correspond to the true class and the columns correspond to the predicted class). To specify the class order for the corresponding rows and columns ofCost, additionally specify theClassNamesname-value pair argument.Structure
Shaving two fields:S.ClassNamescontaining the group names as a variable of the same type asY, andS.ClassificationCostscontaining the cost matrix.
The default is Cost(i,j)=1 if
i~=j, and Cost(i,j)=0 if
i=j.
Example: 'Cost',struct('ClassNames',{{'b','g'}},'ClassificationCosts',[0
0.5; 1 0])
Data Types: single | double | struct
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitcnbuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Prior probabilities for each class, specified as a value in this table.
| Value | Description |
|---|---|
"empirical" | The class prior probabilities are the class relative frequencies
in Y. |
"uniform" | All class prior probabilities are equal to 1/K, where K is the number of classes. |
| numeric vector | Each element is a class prior probability. Order the elements
according to Mdl.ClassNames or
specify the order using the ClassNames name-value
pair argument. The software normalizes the elements such that they
sum to 1. |
| structure | A structure
|
If you set values for both Weights and Prior, the
weights are renormalized to add up to the value of
the prior probability in the respective
class.
Example: Prior="uniform"
Data Types: char | string | single | double | struct
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Score transformation, specified as a character vector, string scalar, or function handle.
This table summarizes the available character vectors and string scalars.
| Value | Description |
|---|---|
"doublelogit" | 1/(1 + e–2x) |
"invlogit" | log(x / (1 – x)) |
"ismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 |
"logit" | 1/(1 + e–x) |
"none" or "identity" | x (no transformation) |
"sign" | –1 for x < 0 0 for x = 0 1 for x > 0 |
"symmetric" | 2x – 1 |
"symmetricismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 |
"symmetriclogit" | 2/(1 + e–x) – 1 |
For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).
Example: ScoreTransform="logit"
Data Types: char | string | function_handle
Observation weights, specified as a numeric vector of positive values or name of a variable in
Tbl. The software weighs the observations in each row of
X or Tbl with the corresponding value in
Weights. The size of Weights must equal the
number of rows of X or Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in Tbl
that contains a numeric vector. In this case, you must specify
Weights as a character vector or string scalar. For example, if
the weights vector W is stored as Tbl.W, then
specify it as "W". Otherwise, the software treats all columns of
Tbl, including W, as predictors or the
response when training the model.
By default, Weights is
ones(, where
n,1)n is the number of observations in X
or Tbl.
The software normalizes Weights to sum up to the value of the prior
probability in the respective class. Inf weights are not supported.
Data Types: double | single | char | string
Hyperparameter Optimization
Parameters to optimize, specified as the comma-separated pair
consisting of 'OptimizeHyperparameters' and one of
the following:
'none'— Do not optimize.'auto'— Use{'DistributionNames','Standardize','Width'}.'all'— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
The optimization attempts to minimize the cross-validation loss
(error) for fitcnb by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitcnb to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitcnb are:
DistributionNames—fitcnbsearches among'normal'and'kernel'.Kernel—fitcnbsearches among'normal','box','epanechnikov', and'triangle'.Standardize—fitcnbsearches amongtrueandfalse.Width—fitcnbsearches among real values, by default log-scaled in the range[1e-3,1e3].
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault
values. For example,
load fisheriris params = hyperparameters('fitcnb',meas,species); params(2).Range = [1e-2,1e2];
Pass params as the value of
OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is the misclassification rate. To control the
iterative display, set the Verbose option of the
HyperparameterOptimizationOptions name-value argument. To control the
plots, set the ShowPlots field of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Optimize Naive Bayes Classifier.
Example: 'auto'
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you must
also specify OptimizeHyperparameters. All the options are optional.
However, you must set ConstraintBounds and
ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Output Arguments
Trained naive Bayes classification model, returned as a ClassificationNaiveBayes model
object or a ClassificationPartitionedModel cross-validated
model object.
If you set any of the name-value pair arguments KFold, Holdout, CrossVal,
or CVPartition, then Mdl is
a ClassificationPartitionedModel cross-validated
model object. Otherwise, Mdl is a ClassificationNaiveBayes model
object.
To reference properties of Mdl, use dot notation.
For example, to access the estimated distribution parameters, enter Mdl.DistributionParameters.
Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. For an example that
shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
More About
In the bag-of-tokens model, the value of predictor j is the nonnegative number of occurrences of token j in the observation. The number of categories (bins) in the multinomial model is the number of distinct tokens (number of predictors).
Naive Bayes is a classification algorithm that applies density estimation to the data.
The algorithm leverages Bayes theorem, and (naively) assumes that the predictors are conditionally independent, given the class. Although the assumption is usually violated in practice, naive Bayes classifiers tend to yield posterior distributions that are robust to biased class density estimates, particularly where the posterior is 0.5 (the decision boundary) [1].
Naive Bayes classifiers assign observations to the most probable class (in other words, the maximum a posteriori decision rule). Explicitly, the algorithm takes these steps:
Estimate the densities of the predictors within each class.
Model posterior probabilities according to Bayes rule. That is, for all k = 1,...,K,
where:
Y is the random variable corresponding to the class index of an observation.
X1,...,XP are the random predictors of an observation.
is the prior probability that a class index is k.
Classify an observation by estimating the posterior probability for each class, and then assign the observation to the class yielding the maximum posterior probability.
If the predictors compose a multinomial distribution, then the posterior probability where is the probability mass function of a multinomial distribution.
Tips
For classifying count-based data, such as the bag-of-tokens model, use the multinomial distribution (e.g., set
'DistributionNames','mn').After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
If predictor variable
jhas a conditional normal distribution (see theDistributionNamesname-value argument), the software fits the distribution to the data by computing the class-specific weighted mean and the unbiased estimate of the weighted standard deviation. For each class k:The weighted mean of predictor j is
where wi is the weight for observation i. The software normalizes weights within a class such that they sum to the prior probability for that class.
The unbiased estimator of the weighted standard deviation of predictor j is
where z1|k is the sum of the weights within class k and z2|k is the sum of the squared weights within class k.
If all predictor variables compose a conditional multinomial distribution (you specify
'DistributionNames','mn'), the software fits the distribution using the bag-of-tokens model. The software stores the probability that tokenjappears in classkin the propertyDistributionParameters{. Using additive smoothing [2], the estimated probability isk,j}where:
which is the weighted number of occurrences of token j in class k.
nk is the number of observations in class k.
is the weight for observation i. The software normalizes weights within a class such that they sum to the prior probability for that class.
which is the total weighted number of occurrences of all tokens in class k.
If predictor variable
jhas a conditional multivariate multinomial distribution:The software collects a list of the unique levels, stores the sorted list in
CategoricalLevels, and considers each level a bin. Each predictor/class combination is a separate, independent multinomial random variable.For each class
k, the software counts instances of each categorical level using the list stored inCategoricalLevels{.j}The software stores the probability that predictor
j, in classk, has level L in the propertyDistributionParameters{, for all levels ink,j}CategoricalLevels{. Using additive smoothing [2], the estimated probability isj}where:
which is the weighted number of observations for which predictor j equals L in class k.
nk is the number of observations in class k.
if xij = L, 0 otherwise.
is the weight for observation i. The software normalizes weights within a class such that they sum to the prior probability for that class.
mj is the number of distinct levels in predictor j.
mk is the weighted number of observations in class k.
If you specify the
Cost,Prior, andWeightsname-value arguments, the output model object stores the specified values in theCost,Prior, andWproperties, respectively. TheCostproperty stores the user-specified cost matrix as is. ThePriorandWproperties store the prior probabilities and observation weights, respectively, after normalization. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.The software uses the
Costproperty for prediction, but not training. Therefore,Costis not read-only; you can change the property value by using dot notation after creating the trained model.
References
[1] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning, Second Edition. NY: Springer, 2008.
[2] Manning, Christopher D., Prabhakar Raghavan, and Hinrich Schütze. Introduction to Information Retrieval, NY: Cambridge University Press, 2008.
Extended Capabilities
This function supports tall arrays with the limitations:
Supported syntaxes are:
Mdl = fitcnb(Tbl,Y)Mdl = fitcnb(X,Y)Mdl = fitcnb(___,Name,Value)[Mdl,AggregateOptimizationResults] = fitcnb(___,Name=Value)—fitcnbadditionally returns theAggregateBayesianOptimizationobjectAggregateOptimizationResults, which contains hyperparameter optimization results when you specify theOptimizeHyperparametersandHyperparameterOptimizationOptionsname-value arguments. You must also specify theConstraintTypeandConstraintBoundsoptions ofHyperparameterOptimizationOptions.
Options related to kernel densities, cross-validation, and hyperparameter optimization are not supported. The supported name-value pair arguments are:
'DistributionNames'—'kernel'value is not supported.'CategoricalPredictors''Cost''PredictorNames''Prior''ResponseName''ScoreTransform''Weights'— Value must be a tall array.
For more information, see Tall Arrays for Out-of-Memory Data.
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitcnb function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2014bfitcnb defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
Starting in R2023b, fitcnb supports the standardization
of predictors with kernel distributions. That is, you can specify the
Standardize name-value argument as true
when the DistributionNames name-value argument includes at
least one "kernel" distribution.
You can also optimize the Standardize hyperparameter by using
the OptimizeHyperparameters name-value argument. Unlike in
previous releases, when you specify "auto" as the
OptimizeHyperparameters value,
fitcnb includes Standardize as an
optimizable hyperparameter.
Starting in R2023b, fitcnb optimizes the kernel smoothing window width of naive Bayes models by using the default search range [1e-3,1e3]. That is, when you specify to optimize the naive Bayes hyperparameter Width by using the OptimizeHyperparameters name-value argument, the function searches among positive values log-scaled in the range [1e-3,1e3].
In previous releases, the default search range for the Width
hyperparameter was
[MinPredictorDiff/4,max(MaxPredictorRange,MinPredictorDiff)], where
MinPredictorDiff and MaxPredictorRange were
determined as follows:
diffs = diff(sort(X));
MinPredictorDiff = min(diffs(diffs ~= 0),[],"omitnan");
MaxPredictorRange = max(max(X) - min(X));MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)