kstest
One-sample Kolmogorov-Smirnov test
Description
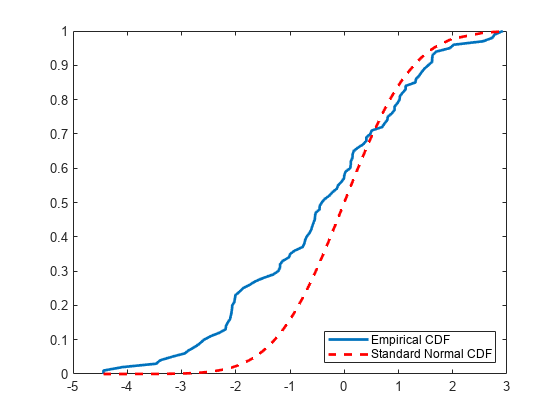
h = kstest(x)x comes
from a standard normal distribution, against the alternative that
it does not come from such a distribution, using the one-sample
Kolmogorov-Smirnov test. The result h is 1 if
the test rejects the null hypothesis at the 5% significance level,
or 0 otherwise.
h = kstest(x,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
kstest decides to reject the null hypothesis
by comparing the p-value p with
the significance level Alpha, not by comparing
the test statistic ksstat with the critical value cv.
Since cv is approximate, comparing ksstat with cv occasionally
leads to a different conclusion than comparing p with Alpha.
References
[1] Massey, F. J. “The Kolmogorov-Smirnov Test for Goodness of Fit.” Journal of the American Statistical Association. Vol. 46, No. 253, 1951, pp. 68–78.
[2] Miller, L. H. “Table of Percentage Points of Kolmogorov Statistics.” Journal of the American Statistical Association. Vol. 51, No. 273, 1956, pp. 111–121.
[3] Marsaglia, G., W. Tsang, and J. Wang. “Evaluating Kolmogorov’s Distribution.” Journal of Statistical Software. Vol. 8, Issue 18, 2003.
Version History
Introduced before R2006a
See Also
kstest2 | lillietest | adtest