Maximum Likelihood Estimation
The mle function computes maximum likelihood estimates (MLEs) for a distribution specified by its name and for a custom distribution specified by its probability density function (pdf), log pdf, or negative log likelihood function.
For some distributions, MLEs can be given in closed form and computed directly. For other distributions, a search for the maximum likelihood must be employed. The search can be controlled with an options input argument, created using the statset function. For efficient searches, it is important to choose a reasonable distribution model and set appropriate convergence tolerances.
MLEs can be biased, especially for small samples. As sample size increases, however, MLEs become unbiased minimum variance estimators with approximate normal distributions. This is used to compute confidence bounds for the estimates.
For example, consider the following distribution of means from repeated random samples of an exponential distribution:
mu = 1; % Population parameter n = 1e3; % Sample size ns = 1e4; % Number of samples rng('default') % For reproducibility samples = exprnd(mu,n,ns); % Population samples means = mean(samples); % Sample means
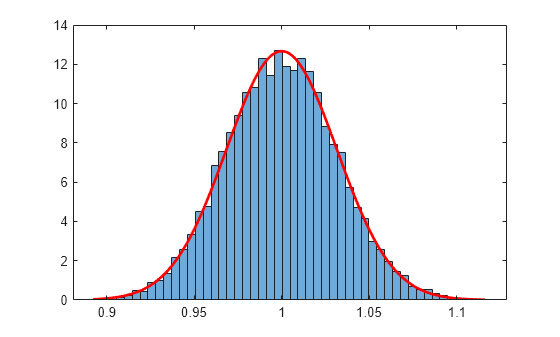
The Central Limit Theorem says that the means will be approximately normally distributed, regardless of the distribution of the data in the samples. The mle function can be used to find the normal distribution that best fits the means:
[phat,pci] = mle(means)
phat = 1×2
1.0000 0.0315
pci = 2×2
0.9994 0.0311
1.0006 0.0319
phat(1) and phat(2) are the MLEs for the mean and standard deviation. pci(:,1) and pci(:,1) are the corresponding 95% confidence intervals.
Visualize the distribution of sample means together with the fitted normal distribution.
numbins = 50; histogram(means,numbins,'Normalization','pdf') hold on x = min(means):0.001:max(means); y = normpdf(x,phat(1),phat(2)); plot(x,y,'r','LineWidth',2)