RegressionGP
Gaussian process regression model
Description
RegressionGP is a Gaussian process regression (GPR) model.
You can train a GPR model, using fitrgp. Using the trained model,
you can
Predict responses for training data using
resubPredictor new predictor data usingpredict. You can also compute the prediction intervals.Compute the regression loss for training data using
resubLossor new data usingloss.
Creation
Create a RegressionGP object by using fitrgp.
Properties
Fitting
FitMethod — Method used to estimate the parameters
'none' | 'exact' | 'sd' | 'sr' | 'fic'
Method used to estimate the basis function coefficients, β; noise standard deviation, σ; and kernel parameters, θ, of the GPR model, stored as a character vector. It can be one of the following.
| Fit Method | Description |
|---|---|
'none' | No estimation. fitrgp uses
the initial parameter values as the parameter values. |
'exact' | Exact Gaussian process regression. |
'sd' | Subset of data points approximation. |
'sr' | Subset of regressors approximation. |
'fic' | Fully independent conditional approximation. |
BasisFunction — Explicit basis function
'none' | 'constant' | 'linear' | 'pureQuadratic' | function handle
Explicit basis function used in the GPR model, stored as a character vector or a function handle. It can be one of the following. If n is the number of observations, the basis function adds the term H*β to the model, where H is the basis matrix and β is a p-by-1 vector of basis coefficients.
| Explicit Basis | Basis Matrix |
|---|---|
'none' | Empty matrix. |
'constant' |
H is an n-by-1 vector of 1s, where n is the number of observations. |
'linear' |
X is the expanded predictor data after
the software creates dummy variables for the categorical variables.
For details about creating dummy variables, see
|
'pureQuadratic' |
where
For this basis option, |
| Function handle | Function handle, where X is an n-by-d matrix of predictors, d is the number of predictors after the software creates dummy variables for the categorical variables, and H is an n-by-p matrix of basis functions. |
Data Types: char | function_handle
Beta — Estimated coefficients
vector
Estimated coefficients for the explicit basis functions, stored
as a vector. You can define the explicit basis function by using the BasisFunction name-value
pair argument in fitrgp.
Data Types: double
Sigma — Estimated noise standard deviation
scalar value
Estimated noise standard deviation of the GPR model, stored as a scalar value.
Data Types: double
CategoricalPredictors — Indices of categorical predictors
vector of positive integers | []
Categorical predictor
indices, specified as a vector of positive integers. CategoricalPredictors
contains index values indicating that the corresponding predictors are categorical. The index
values are between 1 and p, where p is the number of
predictors used to train the model. If none of the predictors are categorical, then this
property is empty ([]).
Data Types: single | double
HyperparameterOptimizationResults — Cross-validation optimization of hyperparameters
BayesianOptimization object | table
This property is read-only.
Cross-validation optimization of hyperparameters, specified as a BayesianOptimization object or a table of hyperparameters and associated
values. This property is nonempty if the 'OptimizeHyperparameters'
name-value pair argument is nonempty when you create the model. The value of
HyperparameterOptimizationResults depends on the setting of the
Optimizer field in the
HyperparameterOptimizationOptions structure when you create the
model.
Value of Optimizer Field | Value of HyperparameterOptimizationResults |
|---|---|
'bayesopt' (default) | Object of class BayesianOptimization |
'gridsearch' or 'randomsearch' | Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst) |
LogLikelihood — Maximized marginal log likelihood
scalar value | []
Maximized marginal log likelihood of the GPR model, stored as a scalar
value if the FitMethod is different from
'none'. If FitMethod is
'none', then LogLikelihood
is empty.
If FitMethod is 'sd',
'sr', or 'fic', then
LogLikelihood is the maximized approximation of
the marginal log likelihood of the GPR model.
Data Types: double
ModelParameters — Parameters used for training
GPParams object
Parameters used for training the GPR model, stored as a GPParams object.
Kernel Function
KernelFunction — Form of the covariance function
'squaredExponential' | 'matern32' | 'matern52' | 'ardsquaredexponential' | 'ardmatern32' | 'ardmatern52' | function handle
Form of the covariance function used in the GPR model, stored as a character vector containing the name of the built-in covariance function or a function handle. It can be one of the following.
| Function | Description |
|---|---|
'squaredexponential' | Squared exponential kernel. |
'matern32' | Matern kernel with parameter 3/2. |
'matern52' | Matern kernel with parameter 5/2. |
'ardsquaredexponential' | Squared exponential kernel with a separate length scale per predictor. |
'ardmatern32' | Matern kernel with parameter 3/2 and a separate length scale per predictor. |
'ardmatern52' | Matern kernel with parameter 5/2 and a separate length scale per predictor. |
| Function handle | A function handle that fitrgp can call like
this:Kmn = kfcn(Xm,Xn,theta)
where Xm is an
m-by-d matrix,
Xn is an
n-by-d matrix, and
Kmn is an
m-by-n matrix of kernel
products such that
Kmn(i,j) is
the kernel product between Xm(i,:)
and Xn(j,:). d
is the number of predictor variables after the software creates dummy
variables for the categorical variables. For details about creating
dummy variables, see CategoricalPredictors.
theta is the
r-by-1 unconstrained parameter vector for
kfcn. |
Data Types: char | function_handle
KernelInformation — Information about the parameters of the kernel function
structure
Information about the parameters of the kernel function used in the GPR model, stored as a structure with the following fields.
| Field Name | Description |
|---|---|
Name | Name of the kernel function |
KernelParameters | Vector of the estimated kernel parameters |
KernelParameterNames | Names associated with the elements of KernelParameters. |
Data Types: struct
Prediction
PredictMethod — Method used to make predictions
'exact' | 'bcd' | 'sd' | 'sr' | 'fic'
Method that predict uses to make predictions
from the GPR model, stored as a character vector. It can be one of
the following.
PredictMethod | Description |
|---|---|
'exact' | Exact Gaussian process regression |
'bcd' | Block Coordinate Descent |
'sd' | Subset of Data points approximation |
'sr' | Subset of Regressors approximation |
'fic' | Fully Independent Conditional approximation |
Alpha — Weights
numeric vector
Weights used to make predictions from the trained GPR model,
stored as a numeric vector. predict computes the
predictions for a new predictor matrix Xnew by
using the product
is the matrix of kernel products between and active set vector A and α is a vector of weights.
Data Types: double
BCDInformation — Information on BCD-based computation of Alpha
structure | []
Information on block coordinate descent (BCD)-based computation of
Alpha when PredictMethod is 'bcd', stored as a
structure containing the following fields.
| Field Name | Description |
|---|---|
Gradient | n-by-1 vector containing the gradient of the BCD objective function at convergence. |
Objective | Scalar containing the BCD objective function at convergence. |
SelectionCounts | n-by-1 integer vector indicating the number of times each point was selected into a block during BCD. |
Alpha property contains the
Alpha vector computed from BCD.
If PredictMethod is not 'bcd',
then BCDInformation is empty.
Data Types: struct
ResponseTransform — Transformation applied to predicted response
'none' (default)
Transformation applied to the predicted response, stored as a character vector describing how
the response values predicted by the model are transformed. In RegressionGP, ResponseTransform is
'none' by default, and RegressionGP does not use ResponseTransform when
making predictions.
Active Set Selection
ActiveSetVectors — Subset of training data
matrix
Subset of training data used to make predictions from the GPR model, stored as a matrix.
predict computes the predictions for a new
predictor matrix Xnew by using the product
is the matrix of kernel products between and active set vector A and α is a vector of weights.
ActiveSetVectors is equal to the training
data X for exact GPR fitting and a subset of
the training data X for sparse GPR methods. When
there are categorical predictors in the model, ActiveSetVectors contains
dummy variables for the corresponding predictors.
Data Types: double
ActiveSetHistory — History of active set selection and parameter estimation
structure
History of interleaved active
set selection and parameter estimation for
FitMethod equal to 'sd',
'sr', or 'fic', stored as a
structure with the following fields.
| Field Name | Description |
|---|---|
ParameterVector | Cell array containing the parameter vectors: basis function coefficients, β, kernel function parameters θ, and noise standard deviation σ. |
ActiveSetIndices | Cell array containing the active set indices. |
Loglikelihood | Vector containing the maximized log likelihoods. |
CriterionProfile | Cell array containing the active set selection criterion values as the active set grows from size 0 to its final size. |
Data Types: struct
ActiveSetMethod — Method used to select the active set
'sgma' | 'entropy' | 'likelihood' | 'random'
Method used to select the active set for sparse methods
('sd','sr', or 'fic'),
stored as a character vector. It can be one of the following.
ActiveSetMethod | Description |
|---|---|
'sgma' | Sparse greedy matrix approximation |
'entropy' | Differential entropy-based selection |
'likelihood' | Subset of regressors log likelihood-based selection |
'random' | Random selection |
The selected active set is used in parameter estimation or prediction,
depending on the choice of FitMethod and PredictMethod in
fitrgp.
ActiveSetSize — Size of the active set
integer value
Size of the active set for sparse methods ('sd','sr',
or 'fic'), stored as an integer value.
Data Types: double
IsActiveSetVector — Indicators for selected active set
logical vector
Indicators for selected active set for making predictions from the
trained GPR model, stored as a logical vector. These indicators mark the
subset of training data that fitrgp selects as the
active set. For example, if X is the original
training data, then ActiveSetVectors =
X(IsActiveSetVector,:).
Data Types: logical
Training Data
NumObservations — Number of observations in training data
scalar value
Number of observations in training data, stored as a scalar value.
Data Types: double
X — Training data
n-by-d table | n-by-d matrix
Training data, stored as an
n-by-d table or matrix, where
n is the number of observations and
d is the number of predictor variables (columns)
in the training data. If the GPR model is trained on a table, then
X is a table. Otherwise, X is
a matrix.
Data Types: double | table
Y — Observed response values
n-by-1 vector
Observed response values used to train the GPR model, stored as an n-by-1 vector, where n is the number of observations.
Data Types: double
PredictorNames — Names of predictors
cell array of character vectors
Names of predictors used in the GPR model, stored as a cell array of
character vectors. Each name (cell) corresponds to a column in
X.
Data Types: cell
ExpandedPredictorNames — Names of expanded predictors
cell array of character vectors
Names of expanded predictors for the GPR model, stored as a cell array
of character vectors. Each name (cell) corresponds to a column in
ActiveSetVectors.
If the model uses dummy variables for categorical variables, then
ExpandedPredictorNames includes the names that
describe the expanded variables. Otherwise,
ExpandedPredictorNames is the same as
PredictorNames.
Data Types: cell
ResponseName — Name of the response variable
character vector
Name of the response variable in the GPR model, stored as a character vector.
Data Types: char
PredictorLocation — Means of predictors
1-by-d vector | []
Means of predictors used for training the GPR model if the training
data is standardized, stored as a 1-by-d vector. If
the training data is not standardized,
PredictorLocation is empty.
If PredictorLocation is not empty, then the
predict method centers the
predictor values by subtracting the respective element of
PredictorLocation from every column of
X.
If there are categorical predictors, then
PredictorLocation includes a 0 for each dummy
variable corresponding to those predictors. The dummy variables are not
centered or scaled.
Data Types: double
PredictorScale — Standard deviations of predictors
1-by-d vector | []
Standard deviations of predictors used for training the GPR model if
the training data is standardized, stored as a 1-by-d
vector. If the training data is not standardized,
PredictorScale is empty.
If PredictorScale is not empty, the predict method scales the
predictors by dividing every column of X by the
respective element of PredictorScale (after
centering using PredictorLocation).
If there are categorical predictors, then
PredictorLocation includes a 1 for each dummy
variable corresponding to those predictors. The dummy variables are not
centered or scaled.
Data Types: double
RowsUsed — Rows of original training data stored
logical vector | []
Rows of the original training data stored in the model, specified as a
logical vector. This property is empty if all rows are stored in
X and Y.
Data Types: logical
Object Functions
compact | Reduce size of machine learning model |
crossval | Cross-validate machine learning model |
lime | Local interpretable model-agnostic explanations (LIME) |
loss | Regression error for Gaussian process regression model |
partialDependence | Compute partial dependence |
plotPartialDependence | Create partial dependence plot (PDP) and individual conditional expectation (ICE) plots |
postFitStatistics | Compute post-fit statistics for the exact Gaussian process regression model |
predict | Predict response of Gaussian process regression model |
resubLoss | Resubstitution regression loss |
resubPredict | Predict responses for training data using trained regression model |
shapley | Shapley values |
Examples
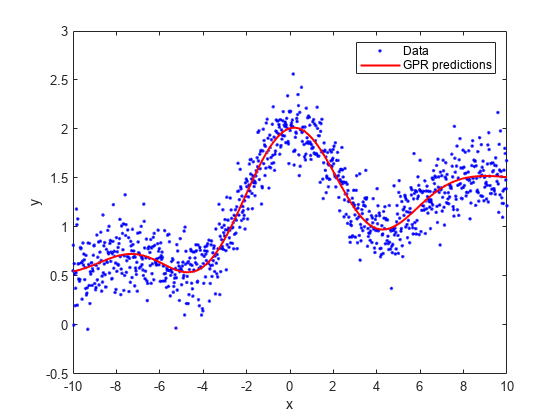
Train GPR Model and Plot Predictions
Generate sample data.
rng(0,'twister'); % For reproducibility n = 1000; x = linspace(-10,10,n)'; y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);
Fit a GPR model using a linear basis function and the exact fitting method to estimate the parameters. Also use the exact prediction method.
gprMdl = fitrgp(x,y,'Basis','linear',... 'FitMethod','exact','PredictMethod','exact');
Predict the response corresponding to the rows of x (resubstitution predictions) using the trained model.
ypred = resubPredict(gprMdl);
Plot the true response with the predicted values.
plot(x,y,'b.'); hold on; plot(x,ypred,'r','LineWidth',1.5); xlabel('x'); ylabel('y'); legend('Data','GPR predictions'); hold off
More About
Active Set Selection and Parameter Estimation
For subset of data, subset of regressors, or fully independent
conditional approximation fitting methods (FitMethod equal to
'sd', 'sr', or 'fic'),
if you do not provide the active set (or inducing input set), fitrgp selects the active set and computes the parameter estimates
in a series of iterations.
In the first iteration, the software uses the initial parameter values in vector η0 = [β0,σ0,θ0] to select an active set A1. The software maximizes the GPR marginal loglikelihood or its approximation using η0 as the initial values and A1 to compute the new parameter estimates η1. Next, the software computes the new loglikelihood L1 using η1 and A1.
In the second iteration, the software selects the active set A2 using the parameter values in η1. Then, using η1 as the initial values and A2, the software maximizes the GPR marginal loglikelihood or its approximation and estimates the new parameter values η2. Then, using η2 and A2, the software computes the new loglikelihood value L2.
The following table summarizes the iterations and the computations at each iteration.
| Iteration Number | Active Set | Parameter Vector | Loglikelihood |
|---|---|---|---|
| 1 | A1 | η1 | L1 |
| 2 | A2 | η2 | L2 |
| 3 | A3 | η3 | L3 |
| … | … | … | … |
The software iterates similarly for a specified number of repetitions. You can specify the
number of replications for active set selection using the
NumActiveSetRepeats name-value argument.
Tips
You can access the properties of this class using dot notation. For example,
KernelInformationis a structure holding the kernel parameters and their names. Hence, to access the kernel function parameters of the trained modelgprMdl, usegprMdl.KernelInformation.KernelParameters.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
The
predictfunction supports code generation.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2015bR2023b: Model stores observations with missing predictor values
Starting in R2023b, training observations with missing predictor values are
included in the X and Y data properties.
The RowsUsed property indicates the training observations
stored in the model, rather than those used for training. Observations with missing
predictor values continue to be omitted from the model training process.
In previous releases, the software omitted training observations that contained missing predictor values from the data properties of the model.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)