Wavelets: Working with Images
This section provides additional information about working with images in the Wavelet Toolbox™ software. It describes the types of supported images and how the MATLAB® environment represents them, as well as techniques for analyzing color images.
Understanding Images in the MATLAB Environment
The basic data structure in MATLAB is the rectangular matrix, an ordered set of real or complex elements. This object is naturally suited to the representation of images, which are real-valued, ordered sets of color or intensity data. (This toolbox does not support complex-valued images.)
The word pixel is derived from picture element and usually denotes a single dot on a computer display, or a single element in an image matrix. You can select a single pixel from an image matrix using normal matrix subscripting. For example:
I(2,15)
returns the value of the pixel at row 2 and column 15 of the image
I. By default, MATLAB scales images to fill the display axes; therefore, an image pixel may
use more than a single pixel on the screen.
Indexed Images
A typical color image requires two matrices: a colormap and an image matrix. The colormap is an ordered set of values that represent the colors in the image. For each image pixel, the image matrix contains a corresponding index into the colormap. (The elements of the image matrix are floating-point integers, or flints, which MATLAB stores as double-precision values.)
The size of the colormap matrix is n-by-3 for an image
containing n colors. Each row of the colormap matrix is a 1-by-3
red, green, blue (RGB) color vector
color = [R G B]
that specifies the intensity of the red, green, and blue components of
that color. R, G, and B are
real scalars that range from 0.0 (black) to 1.0 (full intensity). MATLAB translates these values into display intensities when you display an
image and its colormap.
When MATLAB displays an indexed image, it uses the values in the image matrix to look up the desired color in the colormap. For instance, if the image matrix contains the value 18 in matrix location (86,198), the color for pixel (86,198) is the color from row 18 of the colormap.
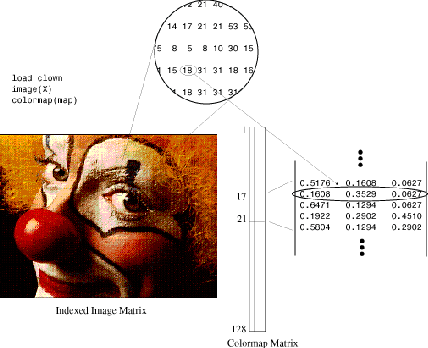
Outside MATLAB, indexed images with n colors often contain values
from 0 to n–1. These values are indices into a colormap with 0 as its first index.
Since MATLAB matrices start with index 1, you must increment each value in the
image, or shift up the image, to create an image that you can
manipulate with toolbox functions.
Wavelet Decomposition of Indexed Images
Indexed images can be thought of as scaled intensity images,
with matrix elements containing only integers from 1 to n, where
n is the number of discrete shades in the image.
Since the image colormap is only used for display purposes, some indexed images may need to be preprocessed to achieve the correct results from the wavelet decomposition.
In general, color indexed images do not have linear, monotonic colormaps and need to be converted to the appropriate gray-scale indexed image before performing a wavelet decomposition.
RGB (Truecolor) Images
An RGB image, sometimes referred to as a truecolor image, is stored in MATLAB as an m-by-n-by-3 data array that defines red, green, and blue color components for each individual pixel. RGB images do not use a palette. The color of each pixel is determined by the combination of the red, green, and blue intensities stored in each color plane at the pixel's location. Graphics file formats store RGB images as 24-bit images, where the red, green, and blue components are 8 bits each. This yields a potential of 16 million colors.
The precision with which a real-life image can be replicated led to the nickname
“truecolor image.” An RGB MATLAB array can be of class double,
single, uint8, or
uint16. In an RGB array of class double,
each color component is a value between 0 and 1.
The color components of an 8-bit RGB image are integers in the range [0, 255] rather than floating-point values in the range [0, 1].
Wavelet Decomposition of Truecolor Images
The truecolor images analyzed are
m-by-n-by-3 arrays of
uint8. Each of the three-color components is a matrix that is
decomposed using the 2-D wavelet decomposition scheme.
Image Conversion
Image Processing Toolbox™ software provides a comprehensive set of functions that let you easily convert between image types. If you do not have Image Processing Toolbox™, this example demonstrates how you can perform conversions using basic MATLAB® commands.
Example 1: Converting Color Indexed Images
Load and display a color indexed image. The color bar to the right of the image is not smooth and does not monotonically progress from dark to light. This type of indexed image is not suitable for direct wavelet decomposition with the toolbox and needs to be preprocessed.
load xpmndrll
whosName Size Bytes Class Attributes X2 192x200 307200 double map 64x3 1536 double
image(X2)
title("Original Color Indexed Image")
colormap(map)
colorbar
First, separate the color indexed image into its RGB components.
R = map(X2,1); R = reshape(R,size(X2)); G = map(X2,2); G = reshape(G,size(X2)); B = map(X2,3); B = reshape(B,size(X2));
Convert the RGB matrices into a gray-scale intensity image, using the standard perceptual weightings for the three-color components.
Xrgb = 0.2990*R + 0.5870*G + 0.1140*B;
Convert the gray-scale intensity image back to a gray-scale indexed image with 64 distinct levels and create a new colormap with 64 levels of gray. The color bar of the converted image is now linear and has a smooth transition from dark to light.
n = 64;
X = round(Xrgb*(n-1))+1;
map2 = gray(n);
figure
image(X)
title("Processed Gray Scale Indexed Image")
colormap(map2)
colorbar
Example 2: Converting RGB TIF Image
Load and display an RGB TIF image.
A = imread("example.tif"); whos A
Name Size Bytes Class Attributes A 650x600x3 1170000 uint8
figure
image(A)
title("Original Image")
colorbar
Convert the image to data type double. Then combine the RGB components into a gray-scale intensity image, using the standard perceptual weightings for the three-color components.
Ad = double(A); Argb = 0.2990*Ad(:,:,1) + 0.5870*Ad(:,:,2) + 0.1140*Ad(:,:,3);
Use the wcodemat function to convert the gray-scale intensity image back to a gray-scale indexed image with 255 distinct levels and create a new colormap with 255 levels of gray.
NbColors = 255;
Aind = wcodemat(Argb,NbColors);
Amap = pink(NbColors);
figure
image(Aind)
colormap(Amap)
title("Processed Image")
colorbar
You can use the same process to convert BMP or JPEG files.
