wavedec2
Multilevel 2-D discrete wavelet transform
Description
[
returns the wavelet decomposition of the matrix C,S] = wavedec2(X,N,wname)X at level
N using the wavelet wname. The output
decomposition structure consists of the wavelet decomposition vector
C and the bookkeeping matrix S, which
contains the number of coefficients by level and orientation.
Note
For gpuArray inputs, the supported modes are
"symh" ("sym") and
"per". If the input is a gpuArray,
the discrete wavelet transform extension mode used by
wavedec2 defaults to "symh"
unless the current extension mode is "per". See the
example Multilevel 2-D Discrete Wavelet Transform on a GPU.
Examples
Input Arguments
Output Arguments
Algorithms
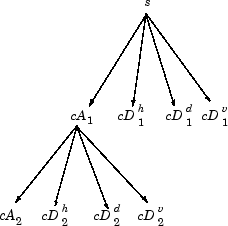
For images, an algorithm similar to the one-dimensional case is possible for two-dimensional wavelets and scaling functions obtained from one-dimensional vectors by tensor product. This kind of two-dimensional DWT leads to a decomposition of approximation coefficients at level j in four components: the approximation at level j+1 and the details in three orientations (horizontal, vertical, and diagonal).
The chart describes the basic decomposition step for images:

where
 — Downsample columns: keep the even-indexed
columns.
— Downsample columns: keep the even-indexed
columns. — Downsample rows: keep the even-indexed rows.
— Downsample rows: keep the even-indexed rows. — Convolve with filter X the rows of
the entry.
— Convolve with filter X the rows of
the entry. — Convolve with filter X the columns of
the entry.
— Convolve with filter X the columns of
the entry.
and
Initialization: cA0 = s.
So, for J = 2, the two-dimensional wavelet tree has the form
References
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
Extended Capabilities
Version History
Introduced before R2006a




